Expansão do número de Euler, sen x e cos x.

KAPLAN-pág.404

  para a=0 e x>0;

 é menor que ou inferior ao n-ésimo termo da série.

pelo critério da razão:

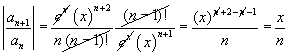
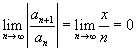
converge para qualquer que seja o x.

PELO CRITÉRIO DO TERMO GERAL

Também vale o argumento para x<0.

Portanto,  pode ser representado por uma série de Taylor.

          (6-46)

para qualquer que seja x.

(Vale lembrar que 0!=1 por definição).

De modo análogo, pode-se provar que são válidas as seguintes expansões:

_{,                         (6-47)}

 para todo x.     (6-48)

, -1<x<1, para todo número real m.                                                                              (6-49)

Próximo tópico: PRINCÍPIO RICO EM APLICAÇÕES

Main Page

Lista dos tópicos sequênciais (disponíveis até o momento):
Para entender a PROVA DA INDENTIDADE DE EULER, siga os tópicos da sequência da lista abaixo.

Princípios de formação de funções
Definição de funções periódicas
Definição de funções harmônicas
Cálculo diferencial para funções transcedentes elementares
Sequências infinitas
Série harmônica
Construção da função do número de Euler
Observações sobre aplicações das séries de Forier
Fórmula de Taylor com resto
Expansão do número de Euler, sen x, cos x.
Princípio rico em aplicações (formação das funções)
Sequências e séries de números complexos para as funções transcedentes elementares
Prova da Identidade de Euler