CONSTRUÇÃO DA FUNÇÃO DO NÚMERO DE EULER

A PARTIR DAS SÉRIES DE MacLaurin e Taylor:

Após ter vistos alguns conceitos de seqüência e séries para seqüências específicas, veremos a seguir, como as seqüências e séries foram exploradas por Taylor e MacLaurin para construção de funções com características especiais. 

A solução dessas funções é o números de Euler, que possui características especiais que permitiram um grande avança no tratamento analítico da matemática.

Desde então, inúmeros problemas da matemática e física puderam ser resolvidos.

Posteriormente será feito uma explicação mais detalhada a respeito.

KAPLAN-pág.399

DEFINIÇÃO DA SÉRIE DE Taylor:

Seja f(x) a soma de uma série de potências cujo intervalo de convergência é   :

  sendo

Essa série denomina-se a série de Taylor de f(x) em x=a se os coeficientes  forem dados pela regra:

,  , , , ..., ,...;

temos então:

 .

KAPLAN-pág.400

DEFINIÇÃO DA SÉRIE DE MacLaurin:

E série de MacLaurin é um caso particular da série de Taylor para a=0. Ou seja:

Por diversos motivos, a manipulação dessa série é mais simples. A substituição de  t=x-a  reduz a série de Taylor geral à forma de uma série de MacLaurin.

KAPLAN-pág.401

Exercício 5: Seja y=f(x)  uma função (caso exista) tal que f(x)  está definida para todo x, f(x) possui uma série de MacLaurin válida para todo x, f(0)=1, e  para todo x.

Mostrar que temos, necessariamente,

e que satisfaça a todas as condição colocadas.

OBSERVAÇÃO:  A função acima é a expansão por série do número de Euler!

Resolução:

Primeiramente, enumeremos as condições colocadas para a função:

Expandindo a função para melhor visualização, temos:

Agora resolvendo a primeira condição: I. f(x) possui um série de MacLaurin válida para todo x.

f(x) para x=0 f(0)=1

Portanto, para

        para x=0 ;

       para x=0 ;

       para x=0 ;

    para x=0 ;

     para x=0 .

Portanto, para qualquer que seja n,   

o que implica que

Em notação matemática:

Para valer a série de MacLaurin para qualquer x pela definição o seu “raio de convergência”  deve ser infinito, ou seja,

Pela definição de raio de convergência:

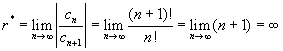
Portanto, a série converge absolutamente para todo x conforme Teorema 35 – KAPLAN-pág.394 Item (6-38).

Resolvendo a segunda condição: II. f(0)=1.

A provar é imediata, bastando substituir x=0 em f(x). O que já foi feito no item anterior!

Resolvendo a terceira condição: III.  ; y=f(x).

Verificando :

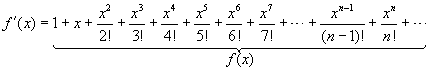
Portanto,

COMENTÁRIOS SOBRE A RESOLUÇÃO DA SÉRIE DE TAYLOR PARA O NÚMERO DE EULER:

A característica que permite que  está baseada nos seguintes fatos:

-         definição dos números fatoriais n!;

-         derivação de  que permite que o resultado seja reduzido em uma ordem e multiplicado pelo número da última ordem;

-         os termos  na série de Taylor serem sempre 1, logo, cada termo da série é definido por: ;

Portanto, sempre que se derivar a função, cada termo da série de potências ficará uma ordem menor e iguala-se com o correspondente termos na função de ordem imediatamente anterior, logo: .

A função demonstrada é o número de Euler.

Provavelmente, este número foi definido por Euler devido a sua característica própria de que  que permite a solução de inúmeros problemas matemáticos principalmente:

-         derivação e integração;

-         substituição (composição de funções), tais como as séries de Forrier;

-         etc.

De fato, na solução de equações da Teoria física do Eletromagnetismo, por exemplo, o número de Euler será empregado intensamente através da “Identidade de Euler”, que será demonstrada posteriormente.

Próximo tópico:  OBSERVAÇÕES SOBRE APLICAÇÕES DAS SÉRIES E FORIER

Main Page

Lista dos tópicos sequênciais (disponíveis até o momento):
Para entender a PROVA DA INDENTIDADE DE EULER, siga os tópicos da sequência da lista abaixo.

Princípios de formação de funções
Definição de funções periódicas
Definição de funções harmônicas
Cálculo diferencial para funções transcedentes elementares
Sequências infinitas
Série harmônica
Construção da função do número de Euler
Observações sobre aplicações das séries de Forier
Fórmula de Taylor com resto
Expansão do número de Euler, sen x, cos x.
Princípio rico em aplicações (formação das funções)
Sequências e séries de números complexos para as funções transcedentes elementares
Prova da Identidade de Euler