Este
texto é parte integrante de um conjunto de textos que objetivam conduzir ao
entendimento das equações aplicadas ao eletromagnetismo.
É um
bom começo para quem quer se aprofundar no assunto.
A
motivação para este artigo consiste no fato de que a “Identidade de Euler” é
utilizada freqüentemente na resolução de Equação Diferenciais Ordinárias –
EDO- aplicadas a fenômenos harmônicos.
Uma
vez que:
as ondas são representadas em geral por funções harmônicas (formadas por senos e co-senos);
em eletromagnetismo há os fasores
– que possuem componentes imaginários;
a
“Identidade de Euler” é utilizada intensamente não somente na solução de
problemas que envolvem ondas como qualquer fenômenos harmônicos (que possuem
oscilações no tempo) em geral. Alguns exemplos de aplicações são citados a
seguir:
física e física matemática em
fenômenos harmônicos;
engenharia mecânica (mecânica
dos fluidos e termodinâmica);
engenharia elétrica e
eletrônica (eletromagnetismo, teoria dos circuitos etc);
engenharia telecomunicações
(processamento de sinais, propagação de ondas etc);
engenharia civil (hidráulica, cálculo estrutural para estrutura
dinâmicas, etc);
todas as demais áreas onde
ocorrem fenômenos harmônicos;
O
bom entendimento da “Identidade de Euler” auxilia, junto com outras operações
matemáticas e estudos de física, no entendimento das equações que regem o
funcionamento de muitos fenômenos da natureza.
Em
termos históricos, pode-se dizer que a “Identidade de Euler”, permitiu o tratamento
analítico da matemática e foi utilizada para resolver vários problemas
matemáticos posteriores, inclusive as Equações de Maxwell que deram origem à
teoria do Eletromagnetismo e das Ondas que foram utilizadas posteriormente como
origem das teorias “ondulatória” e posteriormente na física quânticas por
Einstein.
Em termos matemáticos, a “Identidade de Euler”
adquiri bastante interesse ao relacionar os senos e co-senos com o “Número de
Euler”, cuja “Identidade de Euler” é
dado por:
![]() onde i é o número imaginário.
onde i é o número imaginário.
Ao relacionar o número de Euler com números complexos e as funções trigonométricas seno e co-seno (harmônicas), é criado um artifício matemático que simplifica bastante a solução de Integração e derivação de números complexos, um vez que:
![]() ,ou seja:
,ou seja:
![]() com
com
![]()
conceitos de formação de
funções;
conceitos de funções
periódicas;
definição de funções harmônicas;
conceitos de funções
transcedentes elementares;
conceitos de seqüências
infinitas;
séries harmônicas;
séries de MacLaurin e Taylor
para expansão do números de Euler;
princípio de formação de
funções matemáticas;
demonstração da “Identidade de
Euler” por expansão em séries;
PRINCÍPIOS DE FORMAÇÃO DE
FUNÇÕES
Uma
vez que as funções podem ser representadas por séries que são formadas a partir
de seqüências, para entender a origem (formação) das funções são necessário
conceitos sobre seqüências. Por sua vez, para entender seqüências, são
necessário conceitos sobre as séries.
Portanto,
nos próximos tópicos serão fornecidos conceitos sobre funções importantes e
suas aplicação. A seguir, será abordado gradativamente cada conceito -de
seqüência e de séries- visando atingir um entendimento mais completo sobre as
funções formadas pela Identidade de Euler e, a partir disso, demonstrar sua
validade.
KAPLAN-pag.435
DEFINIÇÃO
DE FUNÇÕES PERIÓDICAS:
Dizemos: f tem um período
![]() . De um modo geral uma função f(x) tal que
. De um modo geral uma função f(x) tal que
![]()
![]() (7-3)
(7-3)
para
to x é dita periódica
com período p. Deve-se notar que cos2x, tem, além do período
![]() , o período
, o período
![]() e, de maneira
genérica, cos
nx e sen nx tem período
e, de maneira
genérica, cos
nx e sen nx tem período
![]() . No entanto
. No entanto
![]() é o único desses período que é compartilhado por todos os
termos da série.
é o único desses período que é compartilhado por todos os
termos da série.
USO
DAS FUNÇÕES PERIÓDICAS:
...
tais funções periódicas aparecem em uma grande variedade de problemas físicos:
vibrações de uma corda, movimento dos planetas ao redor do Sol, rotação da
Terra em torno de seu eixo, movimento de um pêndulo, marés e movimento
ondulatório em geral, vibrações de uma corda de violino, de uma coluna de ar
(por exemplo, numa flauta), e sons musicais em geral. A teoria moderna da luz é
baseada na “mecânica ondulatória”, com vibrações periódicas como
característica; o espectro de uma molécula é simplesmente uma representação das
diferentes vibrações que têm lugar simultaneamente nela. Circuitos elétricos
envolvem muitas variáveis periódicas; por exemplo, a corrente alternada. O fato
de uma viagem ao redor do globo envolverr uma variação total de longitude de
360º é uma expressão do fato de serem as coordenadas cartesianas de posição no
globo funções periódicas da longitude, com período de 360º; muitos outros
exemplos de tais funções periódicas de coordenadas angulares podem ser dados.
FENÔMENOS COM COMPORTAMENTO HARMÔNICOS E FUNÇÕES TRANSCEDENTES ELEMENTARES
KAPLAN-pág.128
Se
f=f(x,y) possuir derivas segundas contínuas num domínio D e se
![]() onde
onde
![]()
em D, então z é chamada harmônica em D. O mesmo termo é usado para uma função de três variáveis que
possui derivadas segundas contínuas num domínio D no espaço e cujo laplaciano é
0 em D. As duas equações que caracterizam as funções harmônicas:
![]() ,
,
![]() ,
,
são chamadas equações de Laplace em duas
e três dimensões, respectivamente.
KAPLAN-pág.129
As
funções harmônicas surgem na teoria dos campos eletromagnéticos, na dinâmica
dos fluidos, na teoria da condução do calor, e em muitas outras partes da
física; algumas aplicações serão discutidas nos Caps. 5, 9 e 10. As funções
bi-harmônicas são usadas sobretudo em elasticidade; elas serão discutidas nos
Caps. 9 e 10.
(comentários)
Muitos
dos fenômenos da natureza possuem oscilações no tempo (periódicos) e podem ser
representadas por funções harmônicas.
As funções harmônicas formadas por composição de senos,
co-senos e polimônios são chamadas de “funções elementares”, pois são formadas
a partir das funções transcedentes elementares, conforme explicado a seguir:
KAPLAN-pag.18
AS FUNÇÕES TRANSCEDENTES
ELEMENTARES:
As
funções senx, cosx e
![]() (onde e=2,71828...) e
suas inversas costuma-se dar o nome de FUNÇÕES TRANSCEDENTES ELEMENTARES.
(onde e=2,71828...) e
suas inversas costuma-se dar o nome de FUNÇÕES TRANSCEDENTES ELEMENTARES.
As funções que são obtidas a partir dessas
últimas e de polinômios, por meio de um número finito de aplicações das
operações aritméticas, de potenciação e de substituições (composição de
funções), recebem o nome de FUNÇÕES ELEMENTARES.
Por
exemplo:
![]()
KAPLAN-pag. 22
CÁLCULO DIFERENCIAL PARA
FUNÇÕES TRANSCEDENTES ELEMENTARES:
Quanto às funções transcedentes elementares, valem:
(0-101)
![]() ;
;
![]() ;
;
![]() ;
;
![]()
As regras para senx e cosx são conseqüências da relação
![]()
que é válida quando os
ângulos são medidos em radianos.
As regras para
![]() e
e ![]() são conseqüências da
relação:
são conseqüências da
relação:
![]() (0-103)
(0-103)
É natural em cálculo tomar e como base
das funções exponenciais e logarítmicas. Então:
![]()
![]() ;
;
![]() com:
com:
![]()
KAPLAN-pag.342
SEQUÊNCIAS INFINITAS:
Se a cada inteiro positivo
n é associado um número
![]() , diz-se que os números
, diz-se que os números
![]() formam uma seqüência infinita. Ordenam-se os números segundos seus índices:
formam uma seqüência infinita. Ordenam-se os números segundos seus índices:
![]()
Exemplos de seqüência são:
![]()
![]()
![]()
Suas regras de formação são:
![]() ,
,
![]() ,
,
![]()
KAPLAN-pág.343
Demonstra-se que as
seqüências (6-1) e (6-2) convergem,
![]()
![]()
![]()
![]()
KAPLAN-pág.356
Teorema 15. A série
harmônica de ordem p.
![]()
converge se p>1 e diverge se
![]() .
.
Demonstração: O termo geral
não converge para 0 (zero) quando
![]() ; portanto, para
; portanto, para
![]() , a série certamente diverge.
, a série certamente diverge.
Para p>0, o critério da integral pode ser usado, tomando-se
![]()
Seja agora
![]() .
.
Uma vez que :
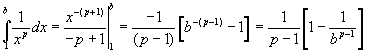
Temos:
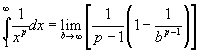
Para
![]()
Para
![]()
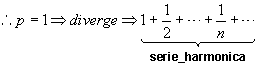
KAPLAN-pág.362
Calcular
![]()
![]()
![]() CRITÉRIO DA RAZÃO
CRITÉRIO DA RAZÃO
![]()
![]()
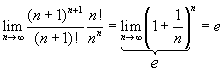 (número de Euler)
(número de Euler)
e>1
![]() série diverge
série diverge
![]() CRITÉRIO DO TERMO GERAL
CRITÉRIO DO TERMO GERAL
![]()
![]()
Na verdade, podemos concluir
desse resultado que
![]()
ou seja, o termo geral tende
ao infinito quando n tende ao infinito.
Definição de SÉRIES DE
POTÊNCIA e RAIO DE CONVERGÊNCIA:
Continuar
a partir do KAPLAN-pág.393.
...
CONSTRUÇÃO DA FUNÇÃO DO
NÚMERO DE EULER
A PARTIR DAS SÉRIES DE
MacLaurin e Taylor:
Após
ter vistos alguns conceitos de seqüência e séries para seqüências específicas,
veremos a seguir, como as seqüências e séries foram exploradas por Taylor e
MacLaurin para construção de funções com características especiais.
A
solução dessas funções é o números de Euler, que possui características especiais
que permitiram um grande avança no tratamento analítico da matemática.
Desde
então, inúmeros problemas da matemática e física puderam ser resolvidos.
Posteriormente
será feito uma explicação mais detalhada a respeito.
KAPLAN-pág.399
DEFINIÇÃO DA SÉRIE DE
Taylor:
Seja
f(x) a soma de uma série de
potências cujo intervalo de convergência é
![]() :
:
![]() sendo
sendo
![]()
Essa
série denomina-se a série de Taylor de f(x) em x=a se os coeficientes
![]() forem dados pela
regra:
forem dados pela
regra:
![]() ,
,
![]() ,
,
![]() ,
,
![]() , ...,
, ...,
![]() ,...;
,...;
temos então:
![]() .
.
KAPLAN-pág.400
DEFINIÇÃO DA SÉRIE DE
MacLaurin:
E série de MacLaurin é um
caso particular da série de Taylor para a=0. Ou
seja:
![]()
Por diversos motivos, a
manipulação dessa série é mais simples. A substituição de t=x-a reduz a série de Taylor geral à forma de uma
série de MacLaurin.
KAPLAN-pág.401
Exercício 5: Seja y=f(x) uma função (caso exista) tal que f(x) está
definida para todo x, f(x) possui uma série de MacLaurin válida para todo x, f(0)=1, e
![]() para todo x.
para todo x.
Mostrar que temos,
necessariamente,
![]()
e que satisfaça a todas as condição colocadas.
OBSERVAÇÃO: A função acima é a expansão por série do número de Euler!
Resolução:
Primeiramente, enumeremos as
condições colocadas para a função:
|
I. |
f(x) possui um
série de MacLaurin válida para todo x. |
|
II. |
f(0)=1 |
|
III. |
|
|
IV. |
|
Expandindo a função para
melhor visualização, temos:
![]()
Agora resolvendo a primeira
condição: I. f(x)
possui um série de MacLaurin válida para todo x.
f(x) para x=0
![]() f(0)=1
f(0)=1
![]()
![]()
![]()
![]()
![]()
Portanto,
para
![]() para x=0
para x=0
![]()
![]() ;
;
![]() para x=0
para x=0
![]()
![]() ;
;
![]() para x=0
para x=0
![]()
![]() ;
;
![]() para x=0
para x=0
![]()
![]() ;
;
![]()
![]() para x=0
para x=0
![]()
![]() .
.
Portanto,
para qualquer que seja n,
![]()
o
que implica que
![]()
Em
notação matemática: ![]()
Para
valer a série de MacLaurin para qualquer x pela
definição o seu “raio de convergência”
![]() deve ser infinito, ou
seja,
deve ser infinito, ou
seja,
![]()
Pela
definição de raio de convergência:
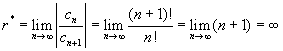
Portanto,
a série converge absolutamente para todo x conforme Teorema 35 – KAPLAN-pág.394 Item (6-38).
Resolvendo
a segunda condição: II. f(0)=1.
A
provar é imediata, bastando substituir x=0 em f(x). O que já foi feito no item anterior!
Resolvendo
a terceira condição: III.
![]() ; y=f(x).
; y=f(x).
![]()
Verificando
:
![]()
![]()
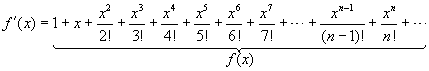
Portanto,
![]()
COMENTÁRIOS
SOBRE A RESOLUÇÃO DA SÉRIE DE TAYLOR PARA O NÚMERO DE EULER:
A
característica que permite que
![]() está baseada nos
seguintes fatos:
está baseada nos
seguintes fatos:
-
definição dos números
fatoriais n!;
-
derivação de
![]() que permite que o
resultado seja reduzido em uma ordem e multiplicado pelo número da última
ordem;
que permite que o
resultado seja reduzido em uma ordem e multiplicado pelo número da última
ordem;
-
os termos
![]() na série de Taylor
serem sempre 1, logo, cada termo da série é definido por:
na série de Taylor
serem sempre 1, logo, cada termo da série é definido por:
![]() ;
;
Portanto,
sempre que se derivar a função, cada termo da série de potências ficará uma
ordem menor e iguala-se com o correspondente termos na função de ordem
imediatamente anterior, logo:
![]() .
.
A
função demonstrada é o número de Euler.
Provavelmente,
este número foi definido por Euler devido a sua característica própria de que
![]() que permite a solução
de inúmeros problemas matemáticos principalmente:
que permite a solução
de inúmeros problemas matemáticos principalmente:
-
derivação e integração;
-
substituição (composição de
funções), tais como as séries de Forrier;
-
etc.
De fato, na solução de
equações da Teoria física do Eletromagnetismo, por exemplo, o número de Euler
será empregado intensamente através da “Identidade de Euler”, que será
demonstrada posteriormente.
KAPLAN-pág.454
(7-6)
OBSERVAÇÕES SOBRE
APLICAÇÕES DAS SÉRIES E FORIER.
O
campo natural de aplicações das séries de Fourier é a de fenômenos periódicos,
como se indicou na Séc.7-1. O fato de uma função periódica poder ser decomposta
em suas componentes harmônicas simples
![]() é de significado
físico fundamental. Para todos os problemas “lineares”, essa resolução permite
reduzir o problema a problemas mais simples de uma única vibração harmônica
simples e depois construir o caso geral por adição (superposição) de simples.
é de significado
físico fundamental. Para todos os problemas “lineares”, essa resolução permite
reduzir o problema a problemas mais simples de uma única vibração harmônica
simples e depois construir o caso geral por adição (superposição) de simples.
A
aplicação concreta das séries de Fourier a tais problemas toma duas formas
fundamentais: uma função periódica f(t) pode ser dada em forma gráfica ou tabelada;
uma compreensão melhor do mecanismo físico que levou a tal função exige uma
“análise harmônica” de f(t), ou seja, representação de f(t) como série de Fourier. Segundo, sabe-se que a função
f(t) é periódica e sabe-se que ela satisfaz a uma
relação, por exemplo a uma equação diferencial; deseja-se determinar f(t) como uma série de Fourier com base nessa informação.
O
primeiro problema é de interpretação de dados
experimentais; o segundo problema é de predição do resultado de uma experiência, com base numa
teoria matemática.
Sendo
a aplicação das séries de Fourier a
fenômenos periódicos fundamental há um campo de aplicação muito mais vasto.
Como se demonstrou acima, uma função “arbitrária” f(x), dada para
![]() , tem uma representação como série de Fourier sobre esse
intervalo. Assim, em qualquer problema relativo a uma função num intervalo pode
ser vantajoso representar a função pela série correspondente. Isso permite uma
enorme variedade de aplicações. Como antes, as aplicações tomam, em geral, a
forma ou interpretação de certos dados, ou de predição funções que satisfaçam
às condições dadas.
, tem uma representação como série de Fourier sobre esse
intervalo. Assim, em qualquer problema relativo a uma função num intervalo pode
ser vantajoso representar a função pela série correspondente. Isso permite uma
enorme variedade de aplicações. Como antes, as aplicações tomam, em geral, a
forma ou interpretação de certos dados, ou de predição funções que satisfaçam
às condições dadas.
KAPLAN-pág.402
FÓRMULA DE TAYLOR COM
RESTO.
A discussão acima (das
séries de Taylor e de MacLaurin) concentrou-se mais nas séries de potências que
nas funções que elas representam. A posição inversa é, também, de grande
importância, e a primeira pergunta que se coloca é esta: dada uma função f(x), com a < x < b se , pode essa função ser representada por uma série de potências nesse
intervalo? Quando f(x) é suscetível de tal
representação, diz-se que f(x) é analítica no
intervalo dado. De modo mais geral, f(x) é
chamada analítica em a < x < b, se para
cada
![]() desse intervalo, f(x)
pode ser representada por uma série de potências em algum intervalo
desse intervalo, f(x)
pode ser representada por uma série de potências em algum intervalo
![]() . A maior parte das funções familiares (polinômios, funções
racionais,
. A maior parte das funções familiares (polinômios, funções
racionais,
![]() , sen x, cos x, log x,
, sen x, cos x, log x,
![]() , e as funções constituídas a partir delas por operações
algébricas e substituições são analíticas em todo intervalo onde a função
examinada é contínua. As exceções não são muito difíceis de reconhecer. Por
exemplo,
, e as funções constituídas a partir delas por operações
algébricas e substituições são analíticas em todo intervalo onde a função
examinada é contínua. As exceções não são muito difíceis de reconhecer. Por
exemplo,
![]() é contínua para todo x, mas possui uma derivada descontínua em x=0. Então a função não pode ser analítica num intervalo
contendo esse valor.
é contínua para todo x, mas possui uma derivada descontínua em x=0. Então a função não pode ser analítica num intervalo
contendo esse valor.
É possível desenvolver facilmente uma teoria satisfatória
de funções analíticas usando-se variáveis complexas.
Contudo, o teorema que segue é bastante útil para
estabelecer a analiticidade de uma função, sem apelo para números complexos.
Teoremo 41. (Fórmula de
Taylor com resto). Seja f(x) uma função.....
.....terminar!!!!
KAPLAN-pág.404
![]()
![]()
![]()
![]() para a=0 e x>0;
para a=0 e x>0;
![]()
![]() é menor que ou
inferior ao n-ésimo termo da série.
é menor que ou
inferior ao n-ésimo termo da série.
![]()
pelo critério da razão:
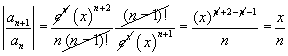
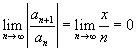
![]() converge para qualquer que seja o x.
converge para qualquer que seja o x.
PELO CRITÉRIO DO TERMO GERAL
![]()
![]()
![]()
![]()
Também vale o argumento para
x<0.
Portanto,
![]() pode ser representado
por uma série de Taylor.
pode ser representado
por uma série de Taylor.
![]()
![]() (6-46)
(6-46)
para qualquer que seja x.
(Vale lembrar que 0!=1 por definição).
De modo análogo, pode-se
provar que são válidas as seguintes expansões:
![]() , (6-47)
, (6-47)
![]() para todo x. (6-48)
para todo x. (6-48)
![]() , -1<x<1, para todo número real m. (6-49)
, -1<x<1, para todo número real m. (6-49)
KAPLAN-pag.408
PRINCÍPIO RICO EM APLICAÇÕES.
Determinação de uma função
que satisfaça uma dada condição.
-
imponha que a
função possa ser expressa por uma série de potências;
-
procure determinar
os coeficientes dessa série de modo tal que seja satisfeita a condição dada;
-
se for possível encontrar
uma série, pode-se examinar a convergência da série e averiguar se, de fato,
ela define uma função que satisfaz à condição dada.
Comentários: Foi
exatamente isso que foi feito ao utilizar a série de MacLaurin fez para
determinar a função que satisfaça as condições iniciais e que definem o número
de Euler.
Veremos mais adiante,
com provar a “Identidade de Euler” que ajudará a resolver integrações e
derivações de números complexos nas equações de eletromagnetismo.
SEQÜÊNCIAS E SÉRIES DE NÚMEROS COMPLEXOS PARA AS
FUNÇÕES TRANSCEDENTES ELEMENTARES:
KAPLAN-pág.413
É particularmente interessante observar que as séries
de potências
(6-46),(6-47),(6-48) de
![]() , sen x e cos x ainda convergem quando se substitui x por
um número complexo arbitrário z, pois, assim, podemos usar as equações
, sen x e cos x ainda convergem quando se substitui x por
um número complexo arbitrário z, pois, assim, podemos usar as equações
![]() , (6-57)
, (6-57)
![]() , (6-58)
, (6-58)
![]() (6-59)
(6-59)
para definir essas
funções no caso complexo. A partir dessas séries, deduzimos a identidade de Euler:
![]() (6-60)
(6-60)
ou a relação mais geral
![]() (6-61)
(6-61)
KAPLAN-pág..414 – Problemas 3 e 4.
3-Provar que as
séries (6-57), (6-58) e (6-59) convergem para todo z.
![]() , (6-57)
, (6-57)
![]() , (6-58)
, (6-58)
![]() (6-59)
(6-59)
Resolução:
Pelo critério da razão
(KAPLAN-pág.357),
Para a série (6-57),
temos:
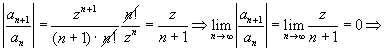 converge absolutamente para qualquer x. Converge absolutamente
converge absolutamente para qualquer x. Converge absolutamente
![]()
Para a série (6-58),
temos:

![]()

![]() converge absolutamente para qualquer x. Converge absolutamente
converge absolutamente para qualquer x. Converge absolutamente
![]()
Para a série (6-59),
temos:
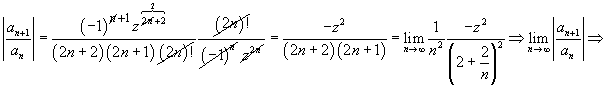

![]() converge absolutamente para qualquer x. Converge absolutamente
converge absolutamente para qualquer x. Converge absolutamente
![]()
KAPLAN-pág.414
Exercícios sobre IDENTIDADE
DE EULER:
4-a) Estabelecer a
IDENTIDADE DE EULER (6-60) a partir da definição de
![]() , sen x e cos x por série.
, sen x e cos x por série.
![]() (6-60)
(6-60)
4-b) Estabelcer a
relação (6-61) a partir da definição de
![]() , sen x e cos x por série.
, sen x e cos x por série.
![]() (6-61)
(6-61)
Resolução:
4-a)
![]() para todo x.
para todo x.
![]() , para todo x.
, para todo x.
![]()
![]()
![]()

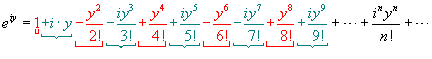
![]()
A expressão de série de
potências é uma conseqüência dessa definição de
![]() complexo para z complexos.
complexo para z complexos.
4-b)