Navigation
Menu
Center-fed Bent-Dipoles
Horizontal Lateral
Vertical
- OCF
Slow-Wave
Other Topics
Home

Such devices use the meander technique. The one on the left is an F-antenna compressed to the side.
The center device is a straight meander monopole compressed to the end.
For hams with a space problem, this type of fitting by bending a wire antenna is not what is usually seen. Typically the most common is the inverted-V, ends bent down and inverted-L forms. Never-the-less, the more complicated meander form is a size reduction alternative to consider if you do not to deal with want loading coils or traps.
How do you "meander" a dipole?
We will start with the most basic definition of a meander as being square. The bottom, sides and top are the same length and at right angles to each other. To "meander" a center-fed wire dipole you need to decide on how many meanders to use on each side. The considerations are: 1.How much space is available for the meander dipole? With square meanders the antenna can theoretically be half length. 2. How much work are you willing to do bending it? More meanders, more stable.
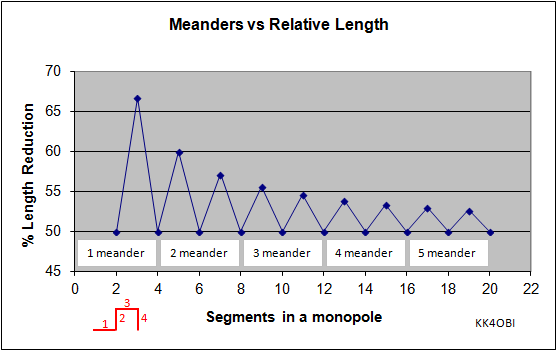
Figure 1
The four segments of a meander are shown in red
In Figure 1 note that if you divide a straight wire into an even number of segments the resulting meander will be 50% of the length of the straight wire. Ten segments would be 3-1/2 meanders as seen in the left USB device in the photo above.
If you divide by an odd number the length reduction will vary because of the end segments will extend from to the sides according to their length. Nine segments per side would result in a meander 56% of the length of a straight wire.
A set of thirteen meanders from 2 to 14 segments per side is presented in this link:
Antenna Design Guide: Meanders vs Relative Length
What are the characteristics
of a "meander" dipole?
of a "meander" dipole?
This question is answered by antenna modeling software. For a dipole with four meanders per side with the standard conditions of #14 AWG fed at 1/2 wavelength feedpoint height, we get:
4NEC2 Antenna Model: Here
Impedance = 29.5 Ohms +j0.26 (Standard dipole = 68.9 +j0.26)
SWR50 = 1.7 (Standard dipole = 1.38)
Radiation Efficiency = 67.5% (Standard dipole = 75.5%)
Gain = 6.66 dBi at 25° elevation above horizontal (Standard dipole = 7.32 dBi at 30°)
Null off ends = -5.5 dBi (Standard dipole = -2.7 dBi) (This is a total difference of 12 dBi between signals from the sides and the ends).
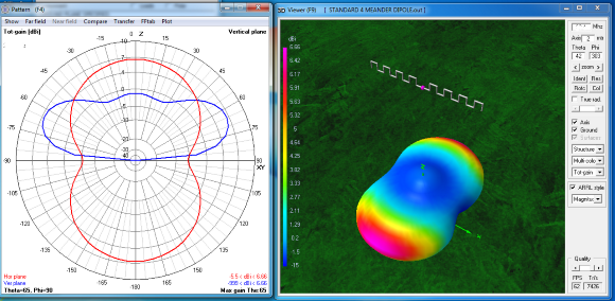
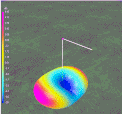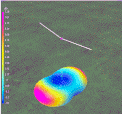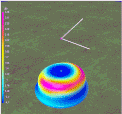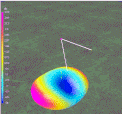
Figure 2
4x4 Meander Dipole
Figure 2 is the Far Field Radiation pattern and 3D flyover view of a 4x4 meander dipole (with four meanders on each arm). Except for the dipole being shorter, the pattern looks the same as a dipole with straight arms but there are differences if we examine the characteristics.
Most noticable change is the drop in impedance down to around 30 Ohms. This means that the lowest SWR obtainable is around 50/30 = 1.7. Workable if miniaturization is needed.
The next most interesting change is the side-to-end ratio that has increased 2 dBi to around 12 dBi signal rejection off ends. In a rotatable dipole with this characteristic is a nice bonus.
The other meander antenna trade-offs are:
- Radiation Efficiency is down 8%.
- Gain is down 0.7 dBi. Both less than a hearable difference.
- More work to build and deploy.

Figure 3

To make the process of meandering a dipole at various frequencies, this table is generalized relative to the length of #14 wire that is resonant at the desired frequency at 1/2 wavelength high feedpoint.
Use the half-wave formula:
150/ MHz = length in meters * 0.9745 wire velocity factor = Resonant Length
Multiply Resonant Length times the Table Value to get actual dimension in meters.
Here is an example for a resonant 10-Meter 4x4 Meander dipole at 28.4 MHz.
Half-wave Formula: 150/28.4 = 5.2817 * 0.9745 wire velocity factor = 5.147 meters
Wire Length = 1.2429 * 5.147 = 6.3972 meters of wire needed at the start. Divide this into two parts = 3.1986 meters each. One for each arm of the dipole.
Segment Size = 0.0388 * 5.147 = 0.1997 meters. The feedpoint is 2 segments wide, 2*0.1997 = 0.3994 meters. Keep that dimension and adjust the center gap for connector or choke.
When finished, the Dipole Length = 0.6214 * 5.147 = 3.193 meters long.
Build Advice: Before bending, measure and mark each bend point. When bending, bend both arms of the dipole at the same time for best precision. For tuning, the Dipole Length can be adjusted either by gap size or by a variable length stub off one end.
What can be done to improve matching
to a 50 Ohm coaxial cable?
to a 50 Ohm coaxial cable?
Only the 0.75 and 6 meander dipoles provide a good match. Dipoles with 1 to 5 meanders have low impedance around 30 ohms and and SWR around 1.7. To solve this problem, the straight forward approach for modeling is to remove the square restraint of horizontal an vertical segments being the same length.
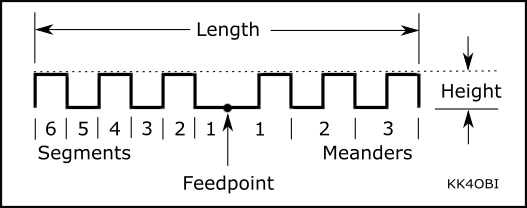
Figure 3
Basics of Meander Antenna Computer Optimization
The software has the ability to systematically adjust Segment Width and Height to find a 50 ohm optimum. To take advantage of this capability, various non-squaremodels were tried. Perfect 1:1 SWR matches for 1 to 5 meander dipoles were found using wider segments and heights around 40% of width. Making meanders higher does not work. This causes causes the impedance to fall.
Figure 4 gives the resulting normalized dimensions.
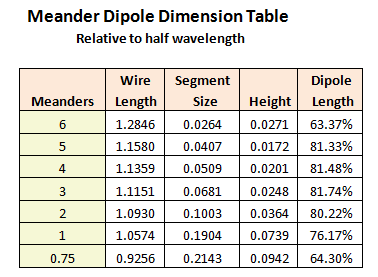
Figure 4
Note that Dipole Length values for 1 to 5 meanders are 80-ish % as long as a straight dipole. Dissapointing. It would be difficult to justify the effort to build one of these low SWR antennas for such a small reduction in length. Consider these studies as an example of how wire antenna modeling can save a lot of wasted effort.
On the other hand, this is where Off Center Feed (OCF) is a much simpler solution for matching square meander dipoles. In this case, placing the feed point at the mid-point of one of the arms of the dipole will give an excellent match for 50 Ohm coaxial cable. Placement is not critical The antenna remains 60-ish % of a straight dipole. However, choke balun should be at or near the feed point to prevent common mode current on the cable.
Suggestions for OCF:
For a 5 Meander dipole, feed at around the 9th segment from center. For a 4 Meander dipole, feed at around the 7.5th segment. For a 3 Meander dipole, feed at around the 6th segment. For a 2 Meander dipole, feed at around the 4th segment. For a 1 Meander dipole, feed between the 2nd and 3rd segments.
This concludes these basic meander computer modeling studies. Althought there are an enormous number of variants developed since the coming of the cell phone, this information should be adequate to introduce this antenna length reduction technique for amateur radio applications.
Dick Reid, KK4OBI at QSL.net