Resonance occurs when the reactance of an inductor balances the reactance of a capacitor at some given frequency. In such a resonant circuit where it is in series resonance, the current will be maximum and offering minimum impedance. In parallel resonant circuits the opposite is true.

Resonance formula

The formula for resonance is:

Which leads us on to:

A particularly simpler formula for radio frequencies (make sure you learn it) is:

Following on from that by using simple algebra we can determine:

In a series resonant circuit the impedance is at its lowest for the resonant frequency whereas in a parallel resonant circuit the impedance is at its greatest for the resonant frequency. See figure 1.

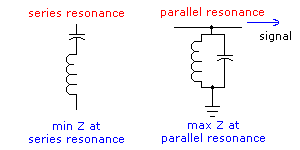
Figure 1 - resonance in series and parallel circuits

"For a series circuit at resonance, frequencies becoming far removed from resonance see an ever increasing impedance. For a parallel circuit at resonance, frequencies becoming far removed from resonance see an ever decreasing impedance".

That was a profoundly important statement. Please read it several times to fully understand it.

A typical example to illustrate that statement are the numerous parallel circuits used in radio. Look at the parallel resonant circuit above. At resonance that circuit presents such a high impedance to the resonant circuit to the extent it is almost invisible and the signal passes by. As the circuit departs from its resonant frequency, up or down, it presents a lessening impedance and progressively allows other signals to leak to ground. At frequencies far removed from resonance, the parallel resonant circuit looks like a short path to ground. For series resonance the opposite is true.

First comes the simple answer. If the demand exists we will provide a complex answer to impedance later.

Now here comes one of the most confusing aspects of electronics - which I will de-mystify by taking an extremely casual approach, so what's new!. I'll keep it dead simple, very inelegant but dead simple and give all the purists heart palpitations. I bet you walk away with a better understanding though.

Assume you have available these 4 items on your bench:

Now if we connect the extremely low wattage bulb to the series string of AA cells we would expect all to work well. Similarly if we connect the high wattage, high-beam headlight to the heavy duty automotive battery all will be well. Well for a time anyway. Both of these sets are "sort"of matched together. Light duty to light duty and heavy duty to heavy duty.

Now what do you think would happen if we connect the high beam headlightto the series AA cells and conversely the low wattage bulb to the automotive battery?.

In the first case we could imagine the high beam headlight would quickly trash our little tiny AA cells. In the second case our min-wattage bulb would glow quite happily at its rated wattage for quite a long time. Why?, therein lies my expanation of impedance. Consider it!

The heavy duty battery is capable of delivering relatively large amounts of power but the series string is capable of delivering onlyrelatively minimal power. The first is a low impedance sourceand the other, in comparison is a relatively high impedance source.

On the other hand the high beam headlight is capable of consuming relatively large amounts of power but the minature bulb is capable of consuming only minimal amounts of power.

High Impedance loads and Low Impedance loads

Again the first is a low impedance load and the other is high impedance load. If you're keen to apply ohms law you will discover why, research it through the text books.

Meanwhile take a well deserved coffee or tea break now and think it over. Me?, I'll just have another beer while I'm waiting for you.

Good break?. If you were paying attention you would now be able to understand an analogy - a particularly rough but effective one;

Imagine a tiny caterpiller chewing on a large blade of grass - no problem plenty to eat there. Now on the other hand imagine a poor cow stuck in a desert with only one similar blade of grass available to eat. I hope you have some better understanding now.

General expression of Impedance

The term impedance is a general expression which can be applied to any electrical entity which impedes the flow of current. Thus this expression could be used to denote a resistance, a pure reactance, or as is most likely in the real world, a complex combination of both reactance and resistance.

Don't get overly concerned if you're a bit confused by that statement at the moment. However this does then lead us on to "Q".