IN3OTD's web site
...under perpetual construction.
LDMOS devices modeling
Under construction...
This page contains some notes about LDMOS devices modeling; while the concepts discussed are general, the main focus is on obtaining models for low/medium power amplifiers for the HF/VHF amateur radio bands.
At first, the small-signal model extraction is discussed and a method is presented that allows to obtain an estimate of the main parameters. The values obtained can then be used as a starting point for an optimization procedure, in order to obtain a model which fits even better the measured data provided as input. Of course, better could have different meanings, so first a measure of the model quality has to be defined; as discussed in [1] several different choices are possible.
Some practical examples of commonly used RF LDMOS are also presented on their own pages (see menu on the left): these model were optimized using the S-parameters Error Vector Magnitude (EVM) as error measure [1].
LTspice is a very popular free SPICE simulator from Linear Technology; while not specifically aimed at RF circuits simulation it can of course be helpful also in that area. For some of the most popular devices a (large signal) LTspice model based on the VDMOS device model has also been extracted; while in general its quality is not exceptional, it can nevertheless be used for a first design evaluation.
Later on also the extraction of a large-signal model, based on [5] and [6], will be presented.
Small-signal model
The following figure shows a typical MOS equivalent circuit
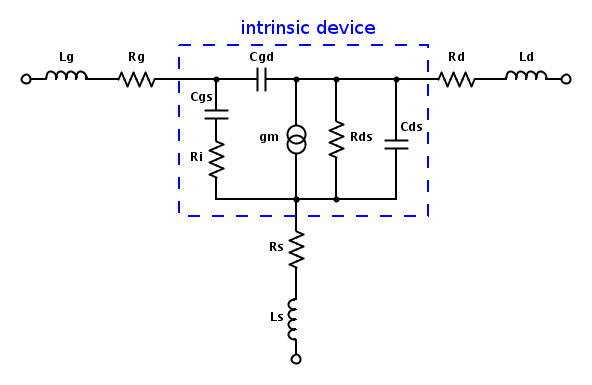
The Z-parameters of this equivalent circuits can be easily determined after some tedious calculations; the general idea is first to compute the Y parameters of the intrinsic part and then add the contributions of the extrinsec resistors and capacitors [2]
Assuming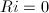 
the Z-parameters are
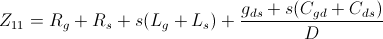
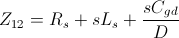
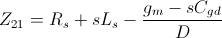
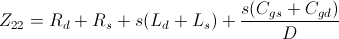where
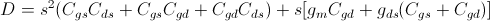
There are a number of different methods to determine parameters values of the small signal model circuit ("parameters extraction"); one of the most general is described in [2]. The Z-parameters above are rewritten as a ratio of polynomials whose coefficient can be determined by fitting these rational functions to the measured Z-parameters;
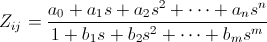Note that some of the Z-parameters equations may need to be multiplied by 
so that all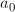 
are non-zero and 
.
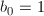An important feature of this method is that a least-square fit can be determined directly, without any iterative optimization needing an initial starting point close enough to the optimal values to converge properly.
For the circuit above, still assuming 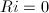, the Z-parameters are rewritten as
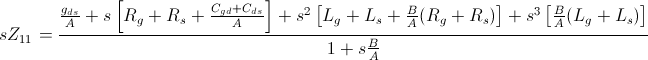
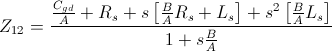
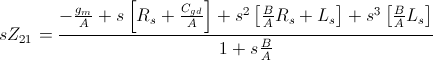
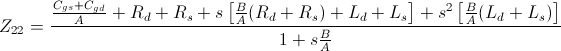note that the denominator of all the expressions is the same.
In the equations above
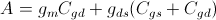
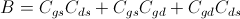so that
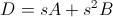
To be continued...
Large-signal model
Under construction...
References: