by Ernst F. Schroeder DJ7HS
CCW is not magic, it is just the application of well-known pieces of communication theory, some which we are not so familiar with. Let me try to explain some of it in the following:
What we generally deal with when 'receiving' CW signals is an electrical signal in
the time domain (i.e. described on the time axis), which does not only and hopefully
contain the wanted signal, but which also is heavily corrupted by added noise and
interference. We more or less intuitively apply the concept of filtering, when we
switch to our best CW filter if conditions and QRM are getting worse. We thus apply what is called 'Wiener filtering'. It is indeed a remarkable result of communication research, that useful filtering can be performed on a completely arbitrary time signal, if only some information on its spectrum (i.e. its representation in the frequency domain) is known.
When we try to examine the spectrum of a CW signal and its bandwidth, we find that most of the energy is contained in a small region about the carrier frequency. For a 60 cpm Morse signal this region is roughly 20 Hz wide (see figure 1).
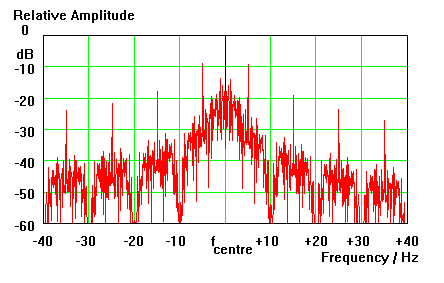 But we can also see, that - at least theoretically - the spectrum extends virtually unlimited on both sides of the carrier. Normally we call this 'keying with clicks' and try to avoid it by using a kind of shaped or rounded keying of the transmitter, instead of switching the carrier on-off instantly.
But we can also see, that - at least theoretically - the spectrum extends virtually unlimited on both sides of the carrier. Normally we call this 'keying with clicks' and try to avoid it by using a kind of shaped or rounded keying of the transmitter, instead of switching the carrier on-off instantly.
We can also see that the amplitude spectrum looks similar within each subdivision of 10 Hz width. By simple reasoning we can conclude that it may be sufficient for the reception of such signals to cut out part of the spectrum with a filter having not more than 20 Hz bandwidth. It indeed is sufficient, and many people have tried to use filters with such bandwidths to increase the readability of CW in heavy QRM. But most of the time the results have been discouraging, mainly because such filters do introduce 'ringing', or more exactly, 'inter-symbol interference'. Therefore we normally use CW filters with bandwidths of 100 ... 300 Hz, but we never get rid of the feeling that there may be a better solution.
Luckily, communication theory has shown that there is one: under some very general assumptions there actually is a true 'best' filter. This filter is characterized in that it has an impulse response (i.e. its definition in the time domain), which is the exact inverse of the time function describing the signal to be detected. Such a method of signal detection is called 'correlation' or 'matched filter' reception. As the basic element of Morse code has a rectangular shape (100 ms duration at 60 cpm), the impulse response of the 'matched' filter also has a rectangular shape, which actually does not change when the time axis is inverted. The frequency response of a filter with such an impulse response does not at all look as nice as what we are used to get from of a good Wiener filter, but it is not the task of this filter to somehow separate the wanted signal from unwanted noise in a way suitable for some human ear. In fact, it does even not make much sense to listen to the output of a correlation filter. Instead, it is its task to maximize the difference in output between signal plus noise and noise alone. The output is then transferred to a decision stage which has to decide between mark and space. This decision then is final, all available information on the signal has been used, and no operation whatsoever on the output can increase the quality of reception further.
Correlation or matched filter detection does work very well as long as we deal with baseband or low-pass signals, such as Morse signals on land lines. But in amateur radio we normally deal with bandpass signals like Morse signals on short waves, in the form of amplitude modulated sinusoids. Theory still holds and the appropriate matched filter for shortwave CW signals has an impulse response consisting of a short train of sinusoid oscillations. Its frequency response is the well-known bumpy characteristic, this time centred on the CW carrier frequency (see figure 2).
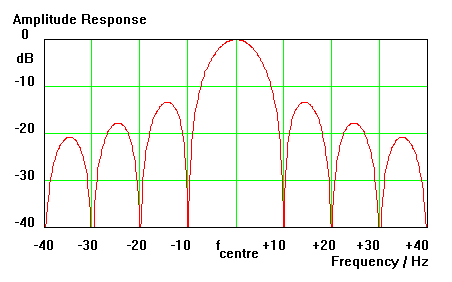
Any real approach to such filtering and detection reveals another problem: it is not only important that the 'matched' impulse response has exactly the same frequency as the transmitted signal, it is also necessary that the signal coming from the transmitter and the filter impulse response generated in the receiver have exactly the same phase! They have to be 'coherent'. Any phase error φ will reduce the filter output proportional to cos(φ), and at a phase error of 90° the output even is completely cancelled. Nevertheless, if we were able to maintain the correct phase relationship, we would have the 'best' possible detection circuit according to some general statistical assumptions. Such a reception and detection method is called 'coherent detection'. Needless to say: this is where 'Coherent CW' got its name from.
Apparently, the price to be paid for having the theoretically best possible reception, is either extreme precision and stability of the system, or a second channel for synchronizing the receiver to the transmitter. But there is a much simpler way to circumvent the problem: We can use two separate receivers which have matched filters with a 90° phase shift relative to each other. Now, in case the output of one receiver is completely cancelled, the other output just gives maximum response. Clever combining of both outputs finally gives one single detection result. The price to be paid is a slightly reduced efficiency (by about 1.5 dB) and twice the receiver hardware. This detection principle has not only been used by the first hardware CCW detection circuits, it is also used by the software CCW detector programs, COHERENT and PRECISION CW.
Funny, but this method is called 'envelope' detection or even 'non-coherent' detection in books on communication theory. Even so, there is no need to find a new name for CCW. Because if not the phase relation between transmitter and receiver, the envelopes and thereby the timings still have to be 'coherent'.
Standard CCW detection for 60 cpm uses matched filters with envelope detection and correlation over a 100 ms time interval. This leads to the well-known characteristic in the frequency domain with nulls every 10 Hz and roughly 2 × 10 Hz bandwidth of the main lobe. If the correlation interval is shortened to 50 ms, then a similar characteristic with nulls every 20 Hz and main-lobe bandwidth of 2 × 20 Hz results. Such a detector is first of all suitable for CCW with 120 cpm, but correct combination of results also enables 60 cpm reception with twice the standard bandwidth. Cutting the correlation interval down to 5 ms enables CCW detection with a main-lobe bandwidth as wide as 2 × 200 Hz. Again, by correct combination of results, all intermediate bandwidths can be utilized. This method is used by PRECISION CW in order to provide a choice of detection bandwidths which are not automatically linked to the CCW speed.
Now, which are those general assumptions which lead to the matched filter concept as the 'best' possible filter? The most important and critical assumption is, that the wanted signal is corrupted by white Gaussian noise only. For experts in communication theory this is an easy limitation, but certainly not for CW operators trying to QSO on a crowded SW band. White Gaussian noise will probably be the limiting factor for EME operators only.
This automatically limits the expectations we should have when applying CCW detection within the short-wave bands, but it does not render CCW completely useless. As experience shows, this form of CW transmission and detection has its benefits, but definitely: miracles should not be expected.
 But we can also see, that - at least theoretically - the spectrum extends virtually unlimited on both sides of the carrier. Normally we call this 'keying with clicks' and try to avoid it by using a kind of shaped or rounded keying of the transmitter, instead of switching the carrier on-off instantly.
But we can also see, that - at least theoretically - the spectrum extends virtually unlimited on both sides of the carrier. Normally we call this 'keying with clicks' and try to avoid it by using a kind of shaped or rounded keying of the transmitter, instead of switching the carrier on-off instantly.
