Constant Wire Comparisons Constant Fractal Comparisons Constant Height Comparisons Constant Band Comparisons Wide Band Comparisons

Constant Wire Comparisons (a stylistic note: all graphics in the table below link to full displays) This is a study of various fractal designs that have one point in common: they all contain identical lengths of wire to construct a second order fractal. Each of the designs is designated by a first order fractal button at the left in the table below. On this page there are two wire lengths observed: 64 meters and 16 meters. No particular care was given to the choice of these dimensions other than their being an order of two. Also, it was a best guess of physical size to serve MF/HF and VHF/UHF. This survey reveals that taking a length of wire and applying almost any folding to it will allow it to retain its spectrum of resonances. By this I mean that it will resonate at intervals roughly matching the resonances of the monopole it is derived from. 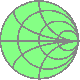64 Meters The table that follows contains Reference and Fractal Antennas SWR spectrums for designs consuming 64 meter of wire. It should be noted that due to the manner in which wire is consumed (bent and turned away from the vertical, or reversed), all fractals are much smaller than 64 meters tall. Observe also that the smaller fractal antennas produce nearly as many resonances as the large radiator. The interesting trend displaying separable features is found in three fractals, the Triadic, M-B Curve, and Z-Fold, showing progressive smoothing of their high Z SWRs in the upper band. The relationships displayed here are a one-to-one correlation of this trend with complexity.

	Reference 64 meter tall Radiator SWR
	3-2 Curve 2nd Order 50 Ohm SWR
	Triadic Koch 2nd Order 200 Ohm SWR
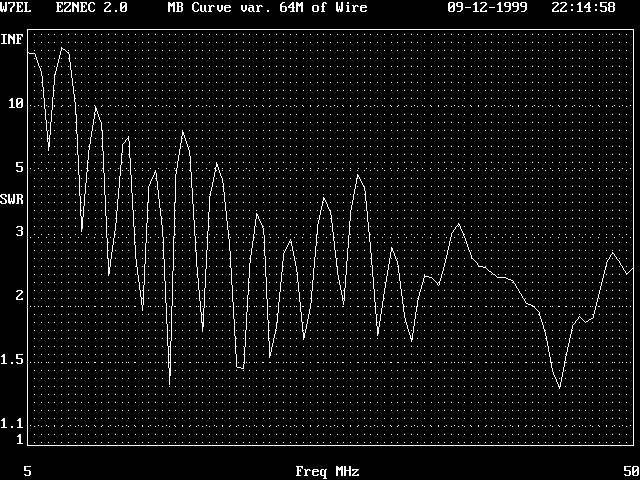
	MB Curve 2nd Order 200 Ohm SWR
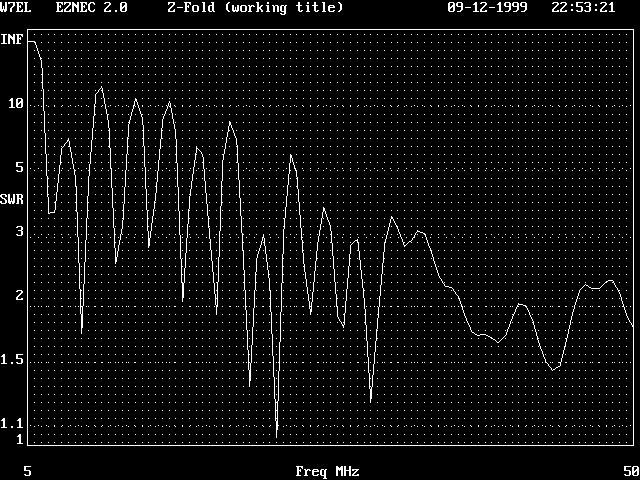
	ZFold 2nd Order 200 Ohm SWR
	Quadratic Koch 2nd Order 200 Ohm SWR

16 Meters

In the following table I have many of the antenna designs above scaled to 16 meters of wire. As always, the first entry is a reference: the 16 meter tall monpole driven against a perfect ground. The remaining entries all consume 16 meters of wire in tracing the fractal shape also driving against a perfect ground. The net result is that each fractal is significantly lower than the standard monopole. The table entries are at SWR minima, a 50 Ohm match is not rare, but by-and-large some minor matching will be required.

The table columns described as x , x element length, H and ordering factor all relate to the physical dimension. x is the number of unit length elements in the first order form. For the monopole it is simply one unit length (the unit being 16 meters). H as you may guess is height to the top of the vertical antenna. You may also note that some fractals have the same x but not the same H. In order to separate out the various designs, the application of H times element length yields my ordering factor.

indicated value is in terms of (resonant frequency in MHz) * (resonant length in Meters)

to find the length of wire in Meters required for resonance, take indicated value and divide by that resonant frequency in MHz

Second Order	x	x element length	H	ordering factor	160M 1-2	80M 2-4	40M 4-8	30M 8-12	20M 12-16	17M 16-20	15M 20-24	12M 24-28	10M 28-32	32-36	36-40	40-44	44-50
16 meter Standard	1	1.00	16	16			72.96		222.4		371.2			521.6		671.9
Sierpinski	2	0.50	8.5	4.25			78.40		232.0			390.4		537.6		688.0
3-2 Curve	3	0.33	7.0	2.31			87.68		251.2			404.8		553.6		707.2
Koch Triadic	4	0.25	9.0	2.25			86.40		249.5			407.2		566.4			718.5
MB Curve	5	0.20	5.7	1.14			97.60			267.2		427.2			580.8		720.0
ZFold	5	0.20	4.0	0.8			93.60			265.6		429.6			589.6		755.2
Koch Quadratic	8	0.125	4.0	0.5			107.2			286.4		449.6			622.4		798.4

Under construction

On the basis of the surveys conducted and presented above, the following "special wire equations" for length of wire consumed in various low SWR antennas have been determined:

First SWR null (0.25 wavelength)

(73 + (1.20 * x) - (0.010 * x²)) / (F₀)

Second SWR null (0.75 wavelength)

(220 + (2.35 * x) - (0.020 * x²)) / (F₀)

Third SWR null (1.25 wavelength)

(371 + (3.10 * x) - (0.030 * x²)) / (F₀)

Fourth SWR null (1.75 wavelength)

(520 + (3.30 * x) - (0.025 * x²)) / (F₀)

Fifth SWR null (2.25 wavelength)

(670 + (3.30 * x) - (0.015 * x²)) / (F₀)

The variable x in all equations is for the number of sections in the structure (corresponding to wires in EZNEC and not segments). These solutions are the best fit to the data provided above and are not suitable for fractal comparisons where the number of elements in any fractal exceeds 50.