Using decibels (dB) to express amplification and attenuation of audio signals, as well as sound intensity
I Z33T home page I страници на македонски јазик I
We experience sound intensity as loudness. The quietest sound that the human ear can detect has an intensity of about 0.000000000001 W/m2, while the loudest sound that can be detected before hearing is damaged is about 1 W/m2.

This means that the loudest sound is a trllion times louder than the quietest sound that we can hear. The human ear cannot distinguish nearly that many sound levels, so using an absolute (linear) scale is impractical. The unit that describes the intensity of sound in a similar way to what the human ear hears is called the decibel (dB
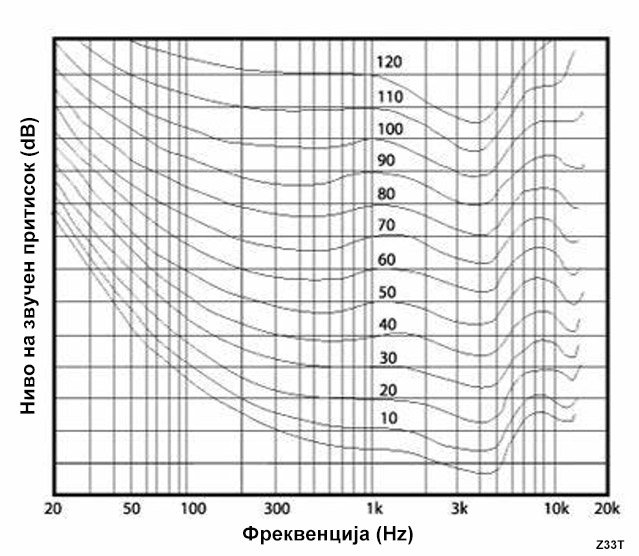
The human sense of hearing is most sensitive to sound with medium frequencies (in the range from 300 Hz to 5000 Hz), shown in the graph above. Lower frequencies (bass) and high frequencies are heard much weaker by humans. This is especially pronounced at low volume, while at higher volume, this dependence decreases and the difference in the perception of low, medium and high tones decreases. When listening to very loud music, the perception of low, medium and high tones is balanced. If we want to listen to quiet music without having a loss of quality in the entire sound spectrum, the low and high tones should be amplified, while the mid tones should remain the same. This perception is achieved with the "Loudness" function that is available on most Hi-Fi amplifiers.
In acoustics, as well as in telecommunications, the gain of an amplifier or the attenuation of an element is expressed in a unit called the decibel (dB).
Also, the sensitivity of loudspeakers, for example, is expressed in a unit called the decibel (dB).

The decibel (dB) is a logarithmic unit used to represent the ratio between two physical quantities.
Decibels can be used to express the ratio between the power of two Hi-Fi amplifiers:
dB = 10 x log (P2/P1)
Decibels can be used to express the ratio between two sound intensities:
dB = 10 x log (I2/I1)
By applying this formula and the logarithmic expression of the sound volume expressed in decibels, the human hearing range is reduced to 120 different levels that correspond to the real perception of the human ear.
Here are some interesting examples that will make the expression in decibels clearer to you:
With each increase in the power of a Hi-Fi amplifier by two times, the power expressed in decibels increases by 3 dB.
With each increase in the power of a Hi-Fi amplifier by four times, the power expressed in decibels increases by 6 dB.
With each increase in the power of a Hi-Fi amplifier by ten times, the power expressed in decibels increases by 10 dB.
With each decrease in the power of a Hi-Fi amplifier by two times, the power expressed in decibels decreases by 3 dB.
With each decrease in the power of a Hi-Fi amplifier by four times, the power expressed in decibels decreases by 6 dB.
With each decrease in the power of a Hi-Fi amplifier by ten times, the power expressed in decibels decreases by 10 dB.
Examples:
- A 100W Hi-Fi amplifier is 3dB more powerful than a 50W Hi-Fi amplifier.
- A 200W Hi-Fi amplifier is 3dB more powerful than a 100W Hi-Fi amplifier.
- A 1000W Hi-Fi amplifier is 3dB more powerful than a 500W Hi-Fi amplifier.
- A 1000W Hi-Fi amplifier is 6dB more powerful than a 250W Hi-Fi amplifier.
- A 1000W Hi-Fi amplifier is 10dB more powerful than a 100W Hi-Fi amplifier.
- A Hi-Fi amplifier with a power of 1000W is 20dB more powerful than a Hi-Fi amplifier with a power of 10W.
- A Hi-Fi amplifier with a power of 1000W is 30dB more powerful than a Hi-Fi amplifier with a power of 1W.
- A Hi-Fi amplifier with a power of 100W is 20dB more powerful than a Hi-Fi amplifier with a power of 1W.
- A Hi-Fi amplifier with a power of 100W is 3dB less powerful than a Hi-Fi amplifier with a power of 200W.
So, if the power of a Hi-Fi amplifier (A) is twice the power of a Hi-Fi amplifier (B), we say that the power of the amplifier (A) is 3 dB more powerful than the power of the amplifier (B).
Here is a table from which you can see this logarithmic dependence and the expression in decibels:

When considering the characteristics of a speaker, one of the most important characteristics is the speaker's sensitivity. Sensitivity is expressed in decibels and indicates how much sound pressure (SPL), expressed in dB, the speaker will produce at a distance of 1m, if the speaker is fed an audio signal with a power of 1W or 2.83 V (2.83 volts of voltage represents 1W of power at a speaker impedance of 8 ohms)
If a speaker produces a sound with an intensity of (for example) 90 dB at a certain distance from the speaker, at a certain amplifier power, then to increase the sound intensity by 3 dB (at the same distance from the speaker) we need to increase the amplifier power by a factor of 2.
If a speaker produces a sound with an intensity of (for example) 100 dB at a certain distance from the speaker, at a certain amplifier power, then to increase the sound intensity by 6 dB (at the same distance from the speaker) we need to increase the amplifier power by a factor of 4.
If a speaker produces a sound with an intensity of (for example) 95 dB at a certain distance from the speaker, at a certain amplifier power, then to increase the sound intensity by 10 dB (at the same distance from the speaker) we need to increase the amplifier power by a factor of 10.

If one speaker has a sensitivity of 90 dB/W/m and another speaker has a sensitivity of 87 dB/W/m, then to play the speakers at the same volume, the first speaker will need half the power from the amplifier than the second speaker, which has 3 dB less sensitivity. For example, the first speaker will need 50W, and the second speaker will need 100W of power from the amplifier to play at the same volume.
If one speaker has a sensitivity of 98 dB/W/m (Klipsch RP-800), and another speaker has a sensitivity of 88 dB/W/m, then to play the speakers at the same volume, the first speaker will need 10 times less power from the amplifier than the second speaker, which has 10 dB less sensitivity. For example, the first speaker will need 50W, and the second speaker will need 500W of power from the amplifier to play at the same volume (of course, if the second speaker can handle that much power)
By using decibels, it is very easy to calculate the ratio between two powers with just simple mathematical operations (addition, subtraction, multiplication and division).
Here are some examples:
1. The difference (ratio) between 1000W and 100W expressed in decibels is 10 dB.
2. The difference (ratio) between 10W and 1W expressed in decibels is 10 dB.
3. The difference (ratio) between 5W and 10W expressed in decibels is 3 dB.
4. The difference (ratio) between 5W and 20W expressed in decibels is 6 dB.
5. The difference (ratio) between 1W and 10W expressed in decibels is 10 dB.
6. The difference (ratio) between 1W and 100W expressed in decibels is 20 dB.
7. The difference (ratio) between 1W and 1000W expressed in decibels is 30 dB.
8. The difference (ratio) between 1W and 2000W expressed in decibels is 33 dB.
9. The difference (ratio) between 1W and 8000W expressed in decibels is 39 dB.
10. The difference (ratio) between 1W and 10000W expressed in decibels is 40 dB.

- - - - - - - - - - - - - - -
Example and task
for those who want to test their knowledge regarding the application of decibels in acoustics:
Let's have a pair of Bowers and Wilkins B&W DM 602 S3 speakers whose sensitivity (SPL) is declared as 90 dB/2.83Vrms/m, and another pair of B&W 607 S2 speakers whose sensitivity (SPL) is declared as 84 dB/2.83Vrms/m. Let the first pair of speakers be connected to an amplifier with a power of 2x10W.
Question: How much power the amplifier connected to the second pair of speakers should deliver so that the sound volume is the same as that of the first pair of speakers?
Answer: The B&W 607 S2 speakers, whose sensitivity (SPL) is declared as 84 dB/2.83Vrms/m, need to be connected to a 2x40W amplifier (4 times the power) to play at the same volume as the first pair of speakers, whose sensitivity is 6 dB higher.
- - - - - - - - - - - - - - - - - - - - - -
Mile Kokotov (2024)
The author has a Master's degree in technical sciences, with almost 45 years of experience in RF, telecommunications and audio engineering.
Check out his other articles and projects on his website.
I Z33T home page I English pages I