next highest and next lowest man-
tissa.
6.986
6.986
7.121 - 10
the given mantissa and the next low-
est mantissa.
5.785
5.887
- 10
significant figures expressed by the
next lower mantissa.
tions are expressed by the following formu-
las:
given characteristic.
log ( a / b )
=
log a - log b
Next lower mantissa
0.7372
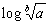
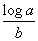
Next lower mantissa
0.7372
log of 1.24
=
0.0934
0.0004
Total
0.6325
than the significant figures expressed by the
lesser mantissa 0.7372 or 546. The sequence
place table. The full answer to this prob-
lem is 305.04.
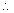 the antilog of 1.7376 = 54.65
the antilog of 1.7376 = 54.65
above, do not exceed four significant figures
in your answer since interpolated results
from a four-place table are not accurate
beyond this point.
Logarithms are added or subtracted like
arithmetical numbers, provided they are
written with positive characteristics. If the
characteristic in the total is greater than 9,
and the notation -10, -20, -30, etc.,
appears after the mantissa, subtract a mul-
tiple of 10 from the positive part and add
the same multiple of 10 to the negative
part, so as to make the resultant character-
istic less than 10.
accurate as can be determined with a four-
place table table. The product of 224 and 4.29
is 960.96
Powers: Find 122 by logarithms:
* 2
2.1584
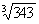
The antilog of 0.8451
=
7.00
cause the logarithms of negative numbers
are imaginary in character, they cannot be
used in computation as with positive num-
bers. However, since the numerical results
of multiplying, dividing, etc., are not
affected by the signs, you can determine the
numerical results by logarithms and later
affix the final + or - signs by inspection.
4.304
7.068
6.284
12.610 - 10
or
2.610
7.764 - 10
9.104 - 10
23.196 - 30
or
3.196 - 10