ALLIED'S ELECTRONICS DATA HANDBOOK

Most Used Formulas (cont.)

To Bottom of Page

Page 17

Return to Table of Contents

HOME
 
Conductance 		   
Admittance
  In direct current circuits, conductance is expressed
  by,
                              
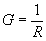
  where      G = conductance in mhos,
                  R = resistance in ohms,
  In d-c circuits involving resistances R1, R2, R3, etc.
  in parallel,
   the total conductance is expressed by
            Gtotal = G1 + G2 + G3 ...etc.
  and the total current by
            Itotal = E Gtotal
  and the amount of current in any single
  resistor, R2 for example, in a parallel group,
  by
                
  R, E and I in Ohm's law formulas for d-c circuits
  may be expressed in terms of conductance as follows:
                          
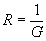
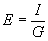
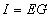
  where      G  =  conductance in mhos,
                  R  =  resistance in ohms,
                  E  =  potential in volts,
                   I  =  current in amperes,
  		    In an alternating current circuit, the admittance of a series
  circuit is expressed by,
                        
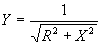
  Admittance is also expressed as the reciprocal of
  impedance, or
                        
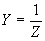
  where      Y = admittance in mhos,
                 R = resistance in ohms,
                 X = reactance in ohms,
                 Z = impedance in ohms,
  R and X in Terms of G and B
    Resistance and reactance may be expressed in terms
  of conductance and susceptance as follows:
                         
  G, B, Y and Z in Parallel Circuits
Susceptance     In any given a-c circuit containing a number of smaller
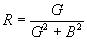
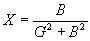
  parallel circuits only,
  
  the effective conductance GT is expressed by
                GT = G1 + G2 + G3...etc.
  
  and the effective susceptance BT by
                BT = B1 + B2 + B3...etc.
  
  and the effective admittance YT by
                  
  
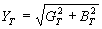
  and the effective impedance ZT by
                  
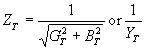
  where       R  =  resistance in ohms,
                  X  =  reactance (capacitive or induc-
                           tive) in ohms,
                  G  =  conductance in mhos,
                   B  =  susceptance in mhos,
                   Y  =  admittance in mhos,
                   Z  =  impedance in ohms,
  In an alternating current circuit, the susceptance of a
  series circuit is expressed by
                         
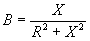
  or, when the resistance is 0, susceptance becomes
  the reciprocal of reactance, or
                         
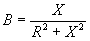
  where    B  =  susceptance in mhos,
               R  =  resistance in ohms,
               X  =  reactance in ohms, 		 

Return to top

 		PAGE 17

Return to Table of Contents

HOME