Transmission Lines
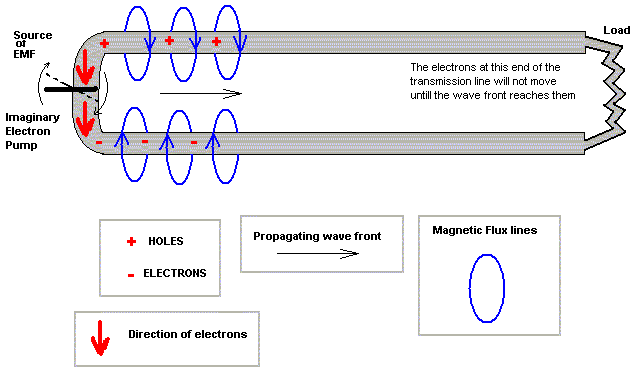
Let’s get back to basics for a moment. With out getting too involved in the atomic theories we'll just say that atoms of metal have the ability to release their outer electrons as long as there is some other electrons nearby to replace the dislodged electron. This exchange of electrons between atoms goes on all of the time in metals but it is very random and chaotic and has no predominate direction. When a metal wire is connected to a source of electro-motive force (EMF) such as a battery or a generator and a complete circuit is made between the positive and the negative terminal of the EMF source then the exchange of electrons is more orderly. They propagate from the negative terminal of the EMF source, through the wire, to the positive terminal of the EMF source. The negative terminal can be said to be pushing the electrons out with a potential pressure while the positive terminal is creating holes or a vacuum for the electrons. The potential difference from the negative to the positive terminal is measured in VOLTS. The word used to describe the rate of electron movement is “current”. If (6.28) X (10 to the 18th power) electrons move past a measuring point in one second, the current is said to be one Ampere or 1Amp. You might also say that there is the same number of holes going the other way.
If the source of EMF is connected to a two wire cable or transmission line and the other end of the line is connected to a load, such as a light bulb or a resistor, then current will flow through both wires at exactly the same time.

Imagine a transmission line of two wires that is several miles long to reach the light bulb or load. Current will begin to flow out of the negative terminal and into the positive terminal of the battery at the instant the wires are connected to the battery, even though current will not be flowing in the wires near the light bulb until a few microseconds later. You may picture the battery as an electron pump that is pushing electrons out of the negative terminal into one wire and at the same instant sucking electrons out of the other wire and into the positive terminal creating holes. As other electrons along the wire rush to fill the holes, more holes are created. The wave of holes tend to propagate along the wire towards the load. Meanwhile on the negative terminal, the wave of excess of electrons is propagating along the other wire toward. the load.
The two wires are side by side in this cable with a charge field between them caused by the difference in potential or pressure of electrons. This charge field of attraction is propagating down the transmission line like a wave toward the light bulb at just under the speed of light.
There is also a magnetic field that surrounds each wire caused by the current flow. The magnetic fields are opposite also because the currents in each wire are opposite in direction. This magnetic field of attraction is also propagating like a wave along the cable towards the light bulb.
The magnetic field has an expanding "front". It is weaker in the very front of the wave field but stronger and constant behind the front. This short rising change in the magnetic field wave generates potential voltage of its own. This "Back EMF" opposes the rise of current at the front while the electric charge at the "front" tends to aid the current. The reactance's of magnetic inductance and EMF charge capacitance is what determines the phenomenal characteristic impedance ("Z") of the cable or transmission line. The formulas, (not shone here), indicate that bigger and closer wires make for lower "Z". Inversely, the "Z" will be greater if the paralleled wires are moved apart or made smaller.
If the length of the line was infinite and the propagating wave front of current and voltage could never reach the end, then the battery or source of EMF would just continue to put electrons into one side and suck them out of the other. Impeded only by the "Z" of the line (and yes slightly by its copper resistance which is very low and not part of this discussion), the battery would be expelling energy into the cable never to see it return.
This imaginary circuit might be measured with an Amp meter and Volt meter at the source. Using the Ohm's Law formula, (R= E/I), the Cable Z could be calculated. Where "E" is the EMF in Volts, "I" is the intensity of current in Amperes and "R" = Resistance in Ohms) the formula would reveal that "R" is equal to the characteristic impedance of the cable. This imaginary infinite length circuit is the only instant where these DC calculations would be imaginarily possible. If the circuit were not infinite in length then the current would be limited by the copper resistance of the wire and the load resistance. In the imaginary circuit of infinite length, the current never reaches the load resistance so the current is limited by the copper resistance of the wires (which is low) and the phenomenal "Z" of the cable.
Of course there is no infinitely long cable, but there could be a very long cable. You could make your measurements very fast or with some sophisticated equipment that would record the voltage and current as time went by. You would see that the measurements would be constant for a while. But after the propagating wave hit the end of the cable and if it found an open circuit. A number of things would then happen.
The rising current "front" would stop. The sudden stop would cause a large rise in voltage due to the collapsing magnetic field. The charging EMF field would also stop and make way for the rise in voltage from the collapsed magnetic field. The new field would begin propagating back towards the source. Some time later the reflected wave front would arrive back at the source and the recording equipment would measure the reflected voltage and current for a short moment of time. The reflected bump in voltage and current might be absorbed by the power source or it might be reflected again. It is possible for the recording equipment to show several back and forth reflections of energy before the absorption from the power source or the line losses consume it.
If the end of the cable has a light bulb or resistor load as a termination load and its resistance is equal to the characteristic impedance of the line, then the original front wave from the battery would be totally absorbed in the load and the recording equipment would show a constant voltage and current with no reflections. Therefore the equipment at the source end of the cable can't tell if the line is infinite in length or just properly terminated.
If at the end of this very long cable there was a short instead of an open then the current would suddenly increase at the point of the load and this would cause a increase in the magnetic field and a drop in potential voltage at the point of the load. Although this is a different change than when the circuit was open there will still ,for the same reasons, be a back wave that will propagate back toward the source. As a matter of fact any load that does not matches the cable "Z" will cause some degree of a back wave.
INTRODUCING AC VOLTAGE INSTEAD OF DC
We have been looking at the instantaneous moments of time as a wave of current and voltage propagate along a transmission line and being started by a DC potential at the source. Instead of attaching a battery to the source end of the line let's connect a high frequency alternating current source. This will send periodic and continuous sine wave pulses of current and voltage along the transmission line towards the load. Again if the load Z is equal to the cable Z then the pulses will be absorbed by the load. With no changes when the pulses reach the load there will be no reflected waves. Another interesting fact is that if measurements of pulse voltage and current were to be made at many different points along the length of the transmission line it would show that all points would measure the same.
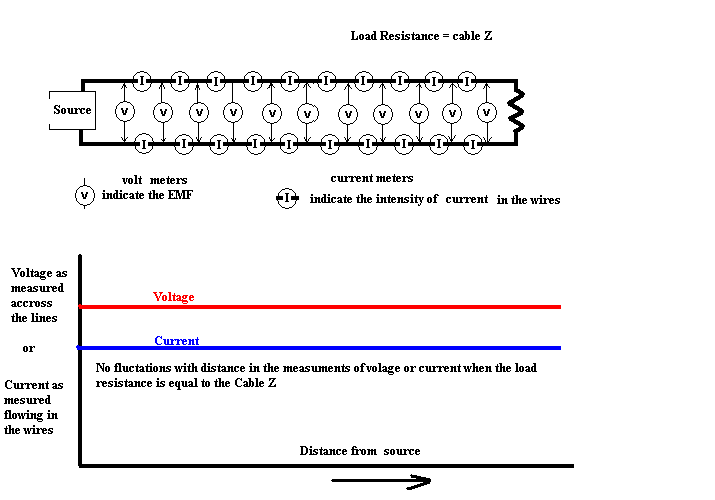
If a graph were to be made where distance from the source was indicated on the horizontal axis and the voltage or current (use a red line for voltage and a blue line for current) was indicated on the vertical axis then the graph would be 2 straight horizontal lines at a height above zero indicative of the voltage or current.
If however if the circuit was open at the load end, then as before the current of the first pulse would suddenly stop causing a reflected wave for that one pulse. The timing of the pulse train coming down the line will determine when and where the reflected wave will collide with the next oncoming wave pulse. At the point of collision the reflected wave will either add to or subtract from the voltage of the oncoming or forward wave pulse. If it is a collision where the voltages are equal then current be very low. However if the collision is at a point where the voltages are opposite then the current will be high and the voltage very low. Assuming that the frequency of the pulses is constant, at evenly spaced periodic points on the line there will be a high voltage / low current pulse followed by low voltage / high current pulse and the points will be the same distance from the ends of the line as long as the frequency of the pulses remain constant. This is known as standing waves. The electrons and holes or still in motions but there are points of high and low intensities along the line coinciding with reflected wave collisions. In the case where the source end of the cable is open there will most certainly be a high voltage standing wave point because no current can flow in the open circuit.
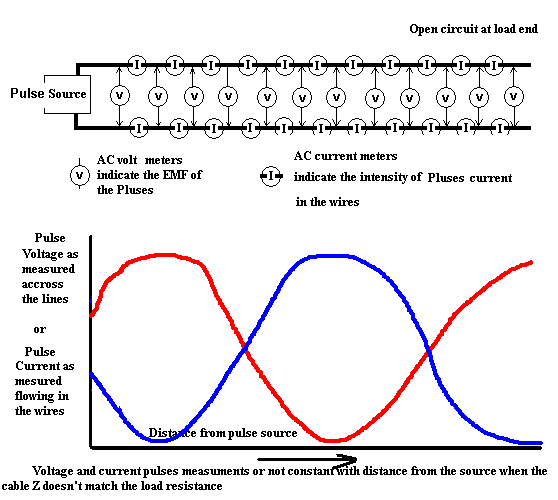
This is of course an extreme mismatch. The other extreme would be if the cable end were shorted. With a short at the end where a load should be the current will be very high and little or no voltage present. Flipping the curve of the current and voltage each upside down or 180 degrees would be indicative of the short circuited load end.
It should be apparent that more complete standing waves will be on the cable if the distance is made longer or the frequency of the pulses higher. The ratio of E/I that the source will see is dependant on the distance from the mismatched load. If the load resistance is not a short or an open but not exactly a match of the cable Z there will still be standing wave variations but they will be less intense. The closer the match of Cable Z to load resistance, the straighter lines will look.
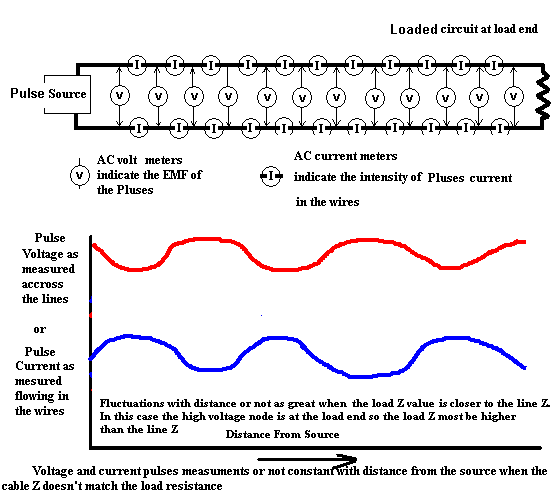
The voltage and current graphs above are exact opposites. In other words the voltage standing wave is exactly 180 degrees out of phase with the current standing wave as for as distance is concerned. This phenomenon will be true as long as the load resistance is purely resistive but if it is reactive as with capacitance or inductance then the phase relationship of the voltage and current standing waves will move accordingly. A 90 degree shift either way would indicate that the load is purely inductive reactance or capacitive reactance and has no resistive load qualities at all.
If a resistive load of 25 ohms is connected via a 50 ohms cable and the length of the cable is physically made to be a multiple of 1/2 wave length for the frequency of the the AC then the source will think it is seeing the 25 ohm resistor because the ratio of E/I of the load will be reflected and reproduced every 1/2 wave length. And there would be no difference as for as the source is concerned.
We might also want the source to see a higher resistance while delivering the power to the 25 ohm load. This could be done by making the transmission line and odd multiple of 1/4 wave length. The source would see 100 ohms but the actual power would still be delivered to the 25 ohm load. This is call a 1/4 wave matching section. We can also place a tuned circuit at the source that will emulate the required distance.
By using certain combinations of inductance and capacitance with equal reactance so the the reactance is canceled, nearly any distance can be emulated. The capacitance and inductance will store the energy and release it at the proper phase so as to appear as a longer or shorter transmission line. High quality air inductors for RF frequencies are very efficient and absorb very little of the RF energy. With this type of design of transmission line and tuner almost any length of transmission line and antenna can be tuned to make a transmitter see the proper match of load that it likes to work into.
This type of combination of inductance and capacitance is call a matching network and in the case of an antenna as the load it is called an antenna tuner. The combination of coil and capacitor values can be chosen or adjusted so that the circuit is made resonate with the transmission line and antenna. In the case of the open wire line and dipole antenna where the line characteristic impedance doesn't match the impedance of the antenna there will certainly be an SWR on the transmission line and the length of the line will determine whether the source end of the line will represent a high or a low impedance and whether it is inductive or capacitive or purely resistive.
One very common matching network is the PiNetwork used quite commonly in tube type transmitters as a way to make a 50 ohm antenna look like a 2 or 3 thousand ohm load to the final amplifier tube circuit. This circuit can of course work backward to make a 2 or 3 thousand ohm antenna system appear as a 50 ohm load for modern transmitters. In some cases where the transmission line is a balanced line as we have been discussing here there needs to a a balun device to change from balanced to unbalanced line. Coaxial cable is unbalanced line where the two conductors are different (shield verses center) whereas twin lead and open wire lines are balanced (two wire of the same type and size running parallel with some type of spacing insulation that maintains the uniform spacing). Generally a balun is a transformer device with a primary and a secondary, or a specially wound and taped coil on a ferrite toroid core. It can also be part of the tuned circuit that will be doing the impedance matching. There must be some method of putting the energy into the device and inductive coupling is as good a method as any and it serves the purpose of the balun as well. below is a method and tuner that I built based on experiances with the Johnson Matchbox and a few others.
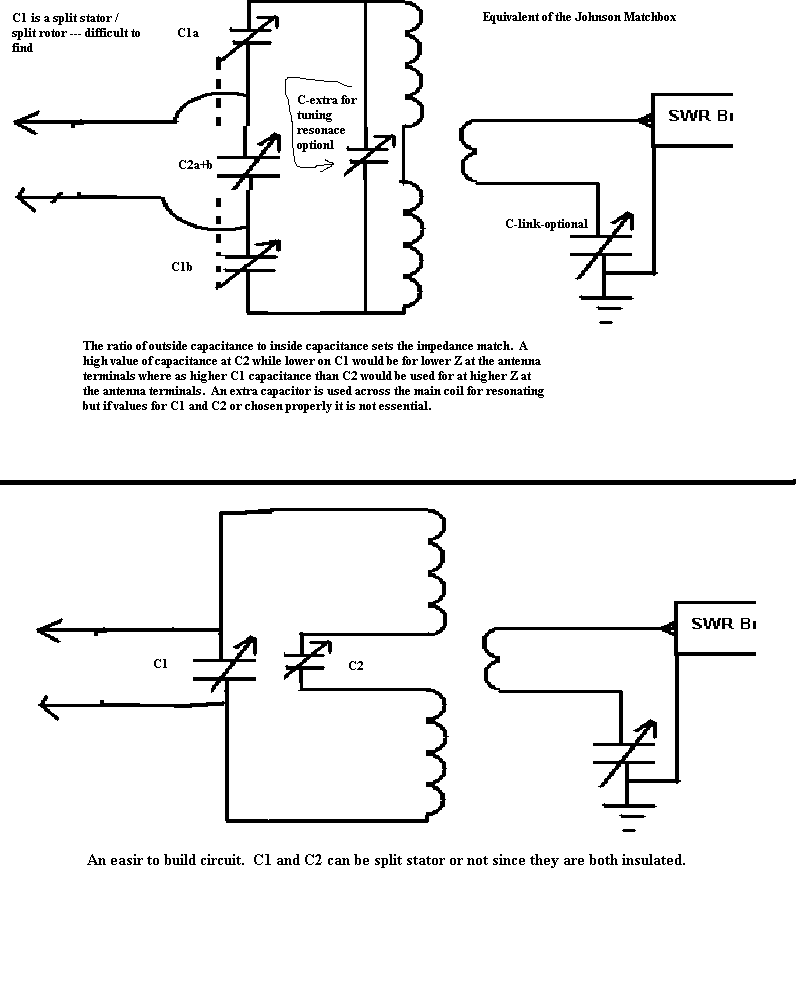
Q is the math function used to describe the ratio of load resistance to reactance of the parallel capacitor. A Q of 10 to 20 is generally good but too high and it will be touchy to tune and the circulating current will be high causing a measurable loss in the parts of the tuner such as heating of the coil or connections. The circuit Q should be high enough to get good energy transfer and tuning to a very low SWR reading on the SWR Bridge meter. L1A and L1B need not be a perfect match but they should be about the same so as to keep stray capacitances distributed equally. L2 should be wound wound around L1Aand B center. A swinging link plug in coil would server very nicely and aid in the adjustment but switching coil taps to achieve the the proper Q and resonance seems to be just as effective. This is the difficult part but the fun part. Not knowing the resistance that may be reflected down the line to the input end of the transmission line makes it is difficult to say what should be used for C2. The best guess is done by determining the length of the line in wave lengths and the dipole in wave lengths. Here are a few examples.
1/2 WAVE Dipole (length = 468 / Freq MHZ) - 75 ohms center fed
1/4 WAVE length open wire line characteristic Z =600 ohms
SWR = 600 : 75 = 8 : 1
1/4 WAVE transformation = SWR * 600 = 4800 ohms
Xc should be about 480 ohms for a Q of 10
Xc should be about 240 ohms for a Q of 20
1/2 WAVE length open wire transmission line will reflect the antenna Z at the feed point. = 75 ohms
********************************************************************************
1 WAVE length dipole center fed = about 2500 ohms (very little data is available on this, accuracy is unknown)
1/4 WAVE length of 600 ohm open wire line
SWR = 600:2500 = 1 : 4.17
1/4 WAVE transformation = SWR * 600 = 144 ohms
1/2 WAVE length open wire transmission line will reflect the antenna Z at the feed point. = 2500 ohms
RF Chokes should be used to remove the static voltage build up on the transmission line and antenna else an arc over might occur during a storm. Placing the RF Chokes in the tuner or outside the tuner on each leg of the transmission line is optional. They may even be moved to the connection of C1 if the RF voltage is lower there, but the chokes should be capable of withstanding the RF Voltage that will be present during transmission. The RF chokes should not detune or offset the balance of the circuit.
There is no theoretical losses due to the use of a tuner and the standing waves on an open wire feed line. There is however the standard loss of energy that is due to the copper resistance and skin effects of the copper wire. These small losses are negligible when using frequencies below 30 MHZ. The losses are increased due to the high current nodes of standing waves on the line but are still negligible. However it is of concern on higher frequencies because there are more nodes for a given length of cable. Dielectric losses of any insulation that might be used to separate the two wires of the cable are always greater at high frequencies and are of major concern in VHF and UHF frequencies.