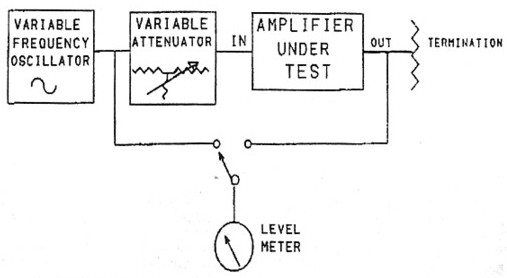
 |
from Selected Spot Frequencies |
Introduction
Frequency or Amplitude Distortion
 |
from Selected Spot Frequencies |
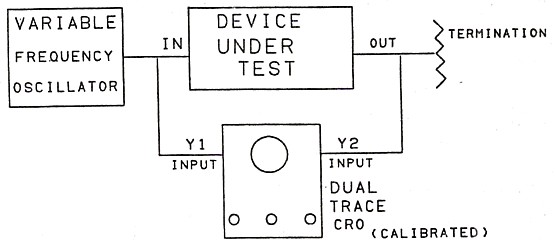 |
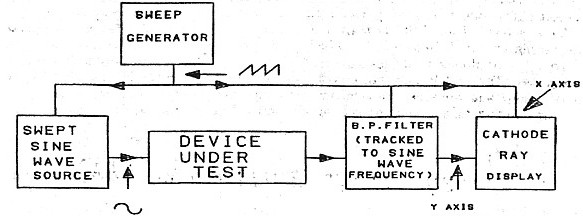 |
a Swept Sine Signal and Spectrum Plot |
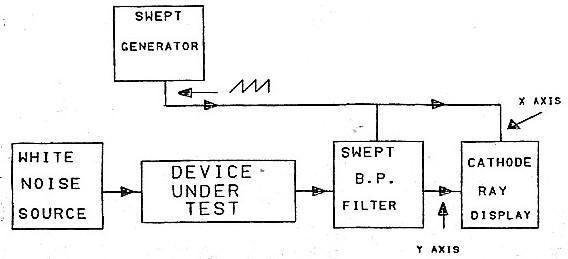 |
a White Noise Source and Spectrum Plot |
Sqare Wave Testing
Harmonic Distortion
Sine Wave Testing
Distortion Meters
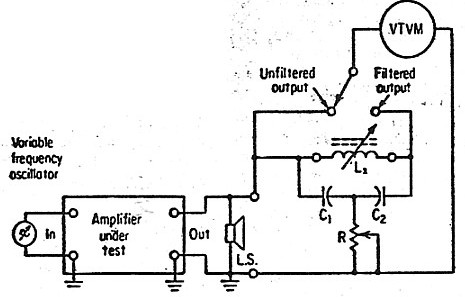 |
showing Bridged T Rejection Filter composed of L2, C1, C2, & R |
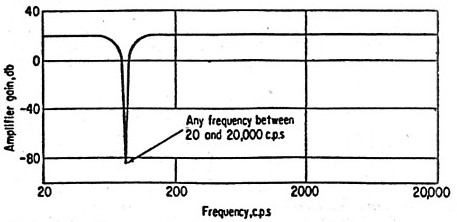 |
in Harmonic Distortion Meter |
|
|
|
|
|
|
Intermodulaton Distortion
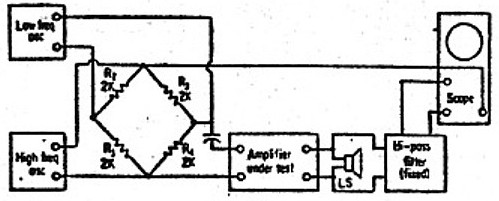 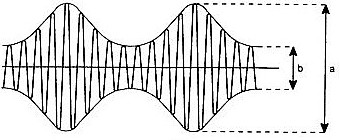
|
Measurement of Phase Shift
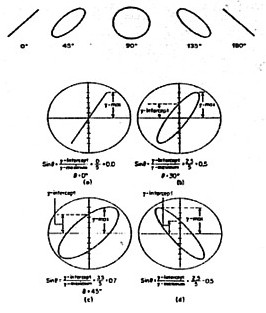
|
Measuring Phase Difference between Two Voltages at the Same Frequency |
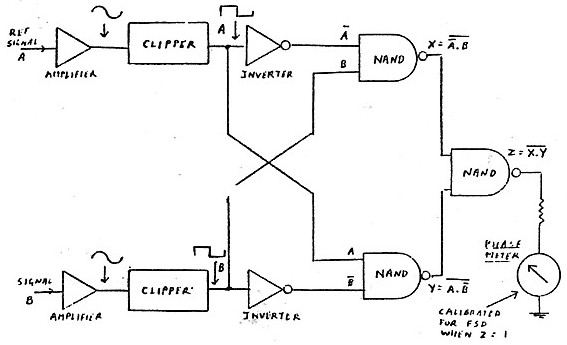 |
 
Figure 22 Digital Waveforms for Different Values of Phase between A and B |
Phase Distortion

|
Sine Squared Pules
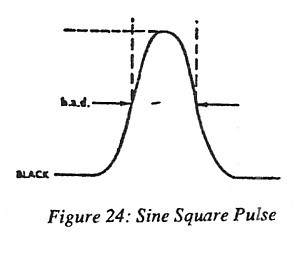
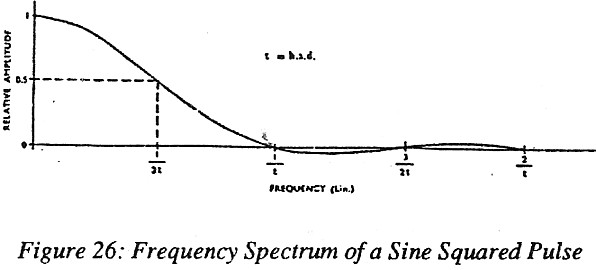 |
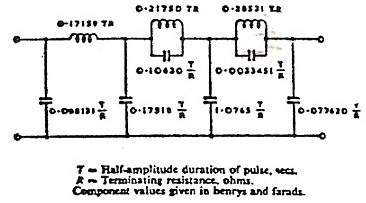 |
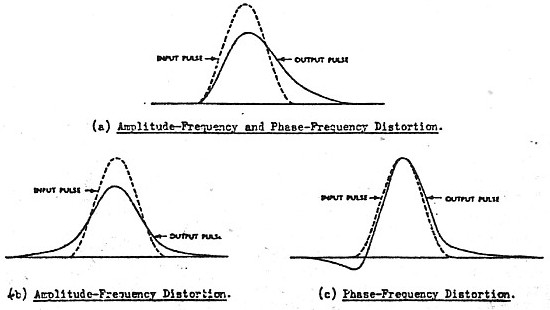
|
The Ultimate Test
References