Introduction
I have often been asked how test instruments common to the radio shack could be used to measure the performance of balanced transmission lines. This is a good question considering that instruments such as the noise bridge and the SWR meter, in their usual form, are made for unbalanced lines with a ground common. Furthermore, the usual SWR meter is made for a balance at 50 ohms, and sometimes 75 ohms, whereas balanced lines, such as TV ribbon and open wire pairs, have a higher characteristic impedance such as 300 ohms. There seems to be little in the amateur radio handbooks addressing this problem so I decided to experiment with a few ideas aimed at using these instruments on balanced lines operating in the HF region.
Initial discussion follows around the use of special balancing circuits which connect to the usual amateur radio noise bridge. The discussion leads on to the SWR meter. In the process of experiment, I constructed a special SWR meter for balanced lines and this instrument will be described. To lead up to this subject, the operation of a typical SWR meter for unbalanced lines is discussed. Whilst there is plenty of available construction information on these instruments, basic theory is often just assumed. Most radio amateurs use these instruments, but I often wonder how many understand the significance of what they measure.
Measurements Through Balun Transformers
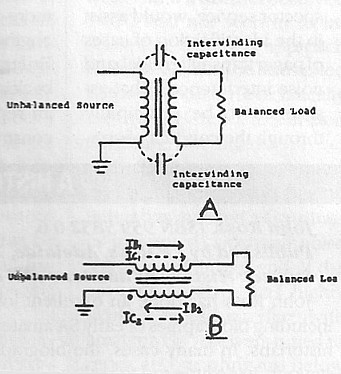
Measurements into balanced lines can be made through a 1:1 RF transformer with primary and secondary tightly coupled. This is easily achieved with the primary and secondary twisted together and wound on a suitable toroidal ferrite or iron dust core. The method of connection shown in figure 1A is not satisfactory for measurement purposes because there is a capacitance unbalance reflected to the secondary from the unbalanced primary. An electrostatic shield between primary and secondary would solve this problem, but be difficult to apply whilst still maintaining tight coupling.

A more satisfactory connection is shown in figure 1B in which each leg of the line is fed through one of the two windings. For the balanced load, the current Ib in each winding is equal but opposite in phase to each other, and the magnetic field is balanced out, resulting in zero inductance. For any common mode signal, the currents Ic1 and 1c2 through the two windings are in phase, hence the device acts as an inductive choke. Furthermore, if there is an unbalance in the load currents Ibl and Ib2 through the windings due to an unbalance of impedance in the load to ground, the device acts as a choke to the differential value of the current (Ib1-Ib2) or (Ib2-Ib1). In effect, the transformer acts as an inductive choke to all but the balanced load current.
The Noise Bridge
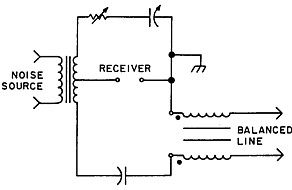
The noise bridge is inherently a device for measuring the reactance and resistance of an RF load with one side grounded. The rotor of its tuning capacitor is grounded and the output to the receiver has one side grounded. I did consider the possibility of a new circuit with the whole bridge floating above ground, but this would have presented some real design problems. However, I found that quite reasonable results could he achieved by connecting the balanced load under test via the choke circuit of figure 1B and as shown in figure 2. For frequencies below 10MHz, I used 12 bifilar turns on an Amidon FT50-72 toroidal ferrite core. The method of winding does introduce some shunt capacitance across the circuit, and five turns were found to be more suitable above 10MHz to reduce error caused by this capacitance.
One problem with the common form of noise bridge is that maximum resistance measurable is limited to 250 ohms or less. The characteristic impedance of ribbon cable and open wire line is usually much higher than this. In my own home-constructed noise bridge, I can switch in extra fixed resistance to allow measurement up to 800 ohms.
An alternative method of measurement is to connect the balanced line via a candelabrum connected balun as shown in figure 3. Two separate transformers, each similar to that of figure 1B are used and an impedance transformation of 4 to 1 is achieved. The circuit is an extension of the figure 1B 1:1 ratio circuit with the inputs of the two transformers in parallel and the outputs in series. Resistance and reactance measurements are indicated on the bridge as a quarter of the real value. For example, 300 ohms resistance would be read as 75 ohms.
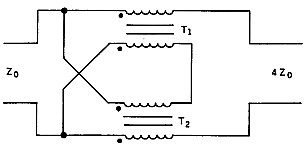
I found the two methods of measurement to be satisfactory on a transmission line provided the line was well balanced such as when terminated in a centre-fed antenna. If some degree of unbalance exists, such as when the line is matched into the end of an antenna, the measured results are in question. In this case, reversing the connecting leads to the line gives a different impedance reading. I suspect the true impedance in the balanced mode is some form of mathematical mean between the two readings, but I am not sure about this.
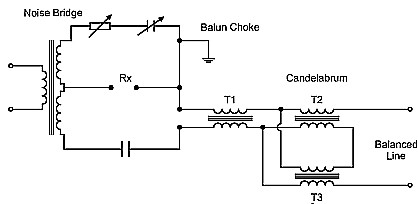
I found that the out-of-balance component could be essentially eliminated by using the candelabrum divide by four circuit, but further isolating its input via another balun choke of figure 1B. The complete system is shown in figure 4. Using this system, the transmission line leads could be reversed without change of reading, even if the line was a little out of balance. I recommend this as the preferred measurement system.
Concerning the toroidal transformer design, the inductive reactance of a winding should be sufficient to act as a choke at the impedance being measured (say 10 times the impedance). On the other hand, as few turns as possible should be used to minimise capacitance between the windings. To achieve high inductance with few turns, a high permeability ferrite core is desirable. The Amidon FT50-72 cores which I used have a permeability of 2000.
Before making any measurement on an actual transmission line, the circuit can be checked out using a resistor of value equal to the characteristic impedance of the line. This will give an indication of the accuracy of the system and whether any appreciable reactance is introduced by the balancing network. This is most important towards 30MHz where the result can be most affected by a small amount of shunt capacity and lead inductance.
The SWR Meter
Before introducing SWR measurement on balanced lines, I thought it would be helpful to first discuss the operating principle of the Standing Wave Ratio (SWR) bridge. Most radio amateurs could explain that the instrument somehow measures forward wave power and reflected wave power, and that it derives a ratio between maximum and minimum of standing wave voltage or current on the transmission line. Let us examine the operation of the instrument in a little more depth.
The instrument operates by comparing two voltages. One voltage is derived from the voltage across the line and is proportional to (and in phase with) that voltage. The other is derived from the current through the line and is proportional to (and in phase with) that current. One type of instrument uses a loop run along in parallel with a length of the line to inductively couple the current component. The voltage component is capacity coupled into the loop. Most SWR meters are also calibrated in power, and this particular instrument, more often used at VHF/UHF, gives a power reading which varies with frequency. Hence it requires a power versus frequency calibration chart.
An SWR meter, which is often assembled by the home constructor,
makes use of a toroidal current transformer to derive the current
sourced voltage component and a resistive voltage divider for the
voltage component. A typical circuit taken from Amateur Radio, Nov
1969 (ref 1) is shown in figure 5. Because of the methods used to
couple each component, the developed voltages are constant with
frequency, and a calibration chart is not required. For this
particular circuit, operation to 70MHz is claimed. For further
explanation of the SWR meter we will make use of this circuit.
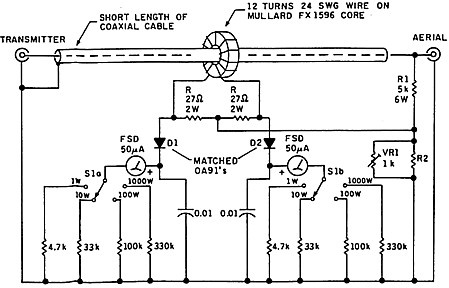 |
|
Figure 5. Typical SWR/Power meter for HF
frequencies (from Amateur Radio, November 1969). |
The voltage derived from current in the line is developed across either of the two 27ohm, resistors marked R. The voltage Vi is calculated as follows:
Vi = Ii.R/T
where Ii is the line current and T is the turns on the secondary of the current transformer. (Note: the primary is, in effect, one turn).
The voltage Vv developed from that across the line is equal to the voltage divider ratio formed by VR1 in parallel with R2 and connected in series with R1. The values of T, R, R1 and R2 in parallel with RV1 are carefully selected so that Vi = Vv when the load resistance is equal to the nominated line impedance (50 or 75 ohms).
Two detector circuits record the summed voltage of Vv and Vi. One, which we will call Forward, adds them directly. The other, which we will call Reverse, adds them, but with Vi reversed in phase. We now refer to the vector diagrams figure 6. If the load is resistive and equal to line impedance, then for Forward, Vv = Vi and the resultant Vr = 2Vv = 2Vi (figure 6A). For Reverse, the resultant is zero (figure 6B) hence the ratio R between Reverse and Forward values of Vr is zero.
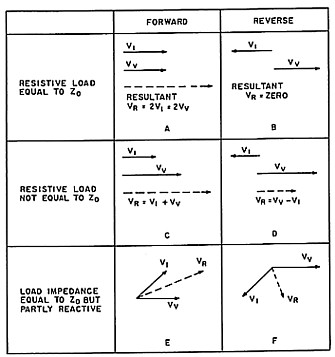
If the load resistance is not equal to Zo, as shown in figures 6C and 6D, a finite value of resultant voltage Vr is developed for Reverse, and the ratio R between Reverse and Forward values of Vr is finite.
A third case (figures 6E and 6F) shows a load impedance equal to Zo, but reactive, hence the load current is out of phase with the load voltage. Again, a finite value of resultant voltage Vr is developed for Reverse, and the ratio R between Reverse and forward values of Vr is finite.
It can be seen that the instrument is a bridge circuit which balances when there is a resistive load equal to Zo and records, by ratio R, the degree by which the load deviates in impedance from that resistive value. When connected to a transmission line, ratio R also equals the ratio between the reflected wave voltage and the incident or forward wave voltage on the line. In operation, transmitted power is set (or meter sensitivity is set) so that the Forward meter reads full scale representing forward wave voltage down the line. The Reverse meter, representing reflected wave voltage, then reads the ratio R between Reverse and Forward values of Vr, hence representing the ratio between reflected and forward wave voltage. The relationship between standing wave ratio SWR and ratio R is given by the formula:
SWR = (1 +R)/(1 -R)
The normal practice is to calibrate the Reverse meter scale in SWR as defined by the formula. The Forward meter is calibrated in power based on E squared divided by Zo where E is the line voltage for an SWR = 1.
Most amateur radio operators of today use an SWR meter, but I venture to say they are used more to ensure that a 50 ohm load is presented to their transmitter than to check SWR on their transmission line. If some form of tuning or matching device is connected between the SWR meter and the transmission line, there is no relationship between what is read on the meter and what standing waves are actually on the line.
How often do we hear on the air someone quoting his SWR = 1:1 to indicate how well his antenna system is adjusted when in fact he is really telling us how well his transmitter is loaded to its correct load impedance? In the next breath he tells us that he is using a Z match or transmatch or whatever and, in reality, has no idea of what standing waves exist on his transmission line, or what power loss they might be causing.
We can use the SWR meter to check the performance of a dummy RF load. We often see a dummy load quoted as having a standing wave ratio of some value at a given frequency. This, of course, is an anomalous declaration. The path length through the core of the dummy load can be considered as but a fraction of a wavelength, hence there are virtually no standing waves. What they really mean is that, using an SWR bridge to check deviation in impedance from the nominal value of dummy load resistance R, a given value on the SWR scale is recorded. It means the impedance load produces a SWR reading similar to a transmission line of Zo = R and operated with that SWR.
So the SWR meter is not really some device which, by some form of magic, separately plucks out the forward wave and the reflected wave to calculate SWR. It is a bridge circuit which records impedance deviation from a given nominal resistance and is calibrated in terms of transmission line SWR.
If it is not obvious, to measure SWR on the transmission line, the meter must face the line. If the line is balanced, or is a different Zo from that for which the meter is designed, some form of transformer is required. As will be discussed in later paragraphs, this addition in itself can produce some questionable readings on the meter.
Owing to loss in the transmission line, the SWR reading will always be higher at the far or antenna end of the line. It is good to check out the far end, but somewhat difficult if located high out in space. If the line is balanced, a balanced SWR meter would seem to be the order of the day. As you will see in the following paragraphs, I have made an effort to design one. I must admit that, up to now, I have stayed at ground level and have not attempted to use it aloft.
Concerning figure 5, I built a unit based on this type of circuit some years ago. For the record, I added a small capacitor across R2 to make the unit balance properly at the upper end of the HF band. This seemed to be necessary to correct for a few picofarads of stray capacity in parallel with R1. This might be a useful tip for someone else building such a unit.
An SWR Meter for Balanced Lines
As part of the balanced line exercise, I set out to build an SWR meter for balanced lines. It seemed a simple matter to base the design on the circuit of figure 5, but with a toroidal current transformer in each leg and a balanced voltage sensing circuit. The outer cover and braid were stripped off some coax cable leaving the centre conductor insulated by the coax dielectric, A length of this was slipped through each toroidal core to form the two legs of the metered transmission line. A short length of braid was ultimately put back over the dielectric where it went through the toroidal core to form an electrostatic shield. I found this was necessary to correct a balance error caused by capacitance coupling into the winding around the core. (Of course, the unbalanced versions such as figure 5 all used the braid shield, so this was not unexpected).
The circuit of the balanced meter is shown in figure 7. The
circuit constants have been worked out for a balance with 300 ohms
resistance, which suits common forms of TV ribbon and open wire
line. The secondaries of the two 10:1 current transformers (T2, T3)
are connected in series. (They also work quite well when connected
in parallel). The voltage divider network (R10 in series with R6/R7
and R8/R9) is coupled into the signal combining and detector/
metering circuit via transformer T4.
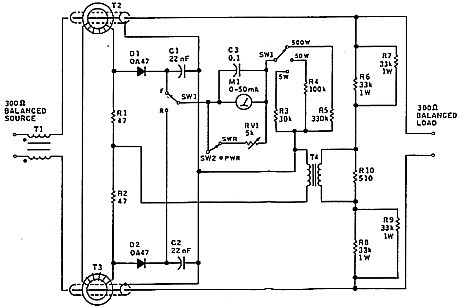 |
|
Figure 7 - VK5BR SWR/power meter for 300 ohm balanced
lines. |
It all seemed straightforward, but I experienced a lot of trouble with circuit balance and common mode currents. I found it necessary to isolate the transmitter source with balun choke Tl to improve the balance at the instrument input. (I should point out that the source was already fed via a standard 4:1 transmitting balun). For T1, a 30mm diameter ferrite core was used to accommodate the transmitter power. This was a high permeability Philips type which I happened to have on hand.
A problem of line balance on some lines showed up as a different SWR value when the line pair legs were reversed. (This was a similar problem to that experienced when using the noise bridge). The problem was compounded by unbalance in the source circuit and hence the reason for the input choke.
Isolating transformer T4 plays an important part in minimising the effects discussed. A conventional transformer connection as in figure 1A seemed more effective for this particular circuit than the choke connection figure 1B.
I tried all sorts of balancing arrangements, but finished with the circuit as shown. Whilst the measurements taken did not completely eliminate response to out-of-balance signal, I decided that the level of this response was reduced enough to be tolerated.
Other Impedances
The balanced SWR meter is designed for a balance at Zo = 300 ohms, but other impedances could be used by changing the value of resistor R10. The value of R10 is inversely proportional to Zo. For example, for Zo = 600 ohms, halve the value of R10. I haven't tried any other impedances, but that is how it can be worked out. For correct power calibration, the meter resistors must also be changed. These are changed in inverse proportion to the square root of the impedance change. For Zo = 600 ohms, divide the meter resistors by root 2.
Checking the Balance
High power 300 ohm non-inductive loads are not easily obtained, but the balance is easily checked by using low transmitter power and loading the SWR meter with a few one or two watt resistors to make up 300 ohms. Five watts on the lowest power select meter position gives full-scale forward reading, and this is applied for just long enough to carry out the test without buming out the resistors. When the meter is selected for reverse or reflected power, the 300 ohm load should give a low meter reading (near 1:1 SWR) at all HF frequencies.
Meter Calibration
The following table can be used to calibrate the meter
scale:
|
SWR uA |
Power uA 0 0 2 10 5 16 10 22 20 32 30 39 50 50 |
75 Ohm SWR Meter with Candelabrum Balun
Although 50 ohms is the most common operating impedance for SWR meters, many have a switch to select either 50 or 75 ohms. The type of meter which uses resistive voltage division (as in figure 5) can also be easily converted to 75 ohms by shunting the lower resistance arm of the voltage divider.
Another method I used for checking SWR on a 300 ohm line was to couple a 75 ohm SWR meter into the line via a 4:1 candelabrum balun pair as shown in figure 8. The toroidal cores of the balun pair needed to be large enough to handle the full RF power which passes through their windings. I used Amidon FC500 FT114 ferrite cores which are 29 mm in diameter. The windings were bifilar wound with 19 turns on each, which gave a calculated inductance of 29 microhenries. This seemed to be a good compromise between sufficient reactance over most of the HF band without too much capacitance.

I found this measuring system worked like a charm. None of the problems I experienced with my balanced SWR meter (figure 7) were apparent, and the transmission line legs could be transposed at will. This seemed to be the best system of measurement, its only limitation being it could be used only at the transmitter end of the line. For measurements at the load or antenna end, the balanced meter would have to be used.
I did try adding a further 1:1 balun choke at the candelabrum input as I had found to be necessary with the noise bridge. However, this did not enhance the performance in any way and, in fact, tended to modify the impedance reflected at the highest frequencies.
One might well ask how the normally used 4:1 impedance ratio balun connection (figure 9) performs as compared with the candelabrum circuit. This connection is a type of auto transformer and probably does little to reject common mode signals. Anyway, when using this type of transformer, I again experienced the problems of a different answer when the line leg pairs were reversed.
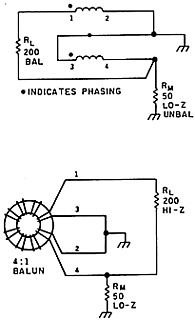
The balun transformer used for figure 9 type balun was the one that can be bought as a 1kW kit with a Amidon T200 iron powder core. Fourteen bifilar turns were placed on the core. When terminated in a 300 ohm resistance, this balun reflected a considerable reactive component at the lower HF frequencies. (This was verified with the noise bridge). Using the 75 ohm SWR meter, the SWR at 21 and 28 MHz was 1.2:1 but increased to 1.8:1 at 7 MHz, and 2.8:1 at 3.5MHz. This compared poorly with my candelabrum circuit, which gave a reading within 1.1:1 over the whole range of 3.5 to 28MHz.
Now this is an interesting result. Suppose you use this typical broadband balun at, say, 3.5MHz to couple to a transmission line and then adjust your matching at the antenna end by stub or whatever. You adjust for a 1:1 SWR on the meter, but actually achieve a mismatch and standing waves on the line. Of course, the core needs more turns for the lower frequencies. Some time ago I did some tests with this core using the 1:1 ratio winding connection and a 50 ohm load. I came to the conclusion that, for better performance, the number of turns should be increased to around 20 for frequencies below 5MHz and reduced to around six turns for frequencies above 10MHz. Anyway, there is a message here. Do not take your balun transformer for granted. Check it out at the frequency of operation using the SWR meter and with its secondary terminated in a dummy resistance equal to working load impedance. Fortunately, even if mismatched, line losses at the lower HF frequencies are small, hence we are usually able to tolerate the effect I have discussed without recourse to rewinding the transformer.
Summary
Based on much of my own experimentation, I have described how common instruments in the radio shack can be used to make impedance and SWR measurements on balanced transmission lines. Measurement methods involve the use of particular types of balancing circuits which work in conjunction with the noise bridge and the SWR meter. A specific SWR meter for 300 ohm balanced lines is also described. Included in the discussion is a description of how an SWR meter works, and some comments on how it is generally used in the radio shack.
I think there is material in this article to invite further discussion on the measurement of balanced lines and the use of the two instruments put to use. Perhaps some of our readers have some other ideas which I hope they can test out before going to print. It is one thing to put up a theory, but I found this particular project (simple as it may seem) was one with plenty of those hidden little difficulties.
References
1. PG Martin G3PDM Frequency Independent Directional Wattmeter and SWR Meter - Amateur Radio, November 1969.
2. Lloyd Butler VK5BR - The Merits of Open Wire Lines Amateur Radio, Sept 1991.
3. Lloyd Butler VK5BR - Transmission Lines Measurements of their Characteristics -Amateur Radio, October 1989.