(Originally published in Amateur Radio, October 1989)
 |
(Originally published in Amateur Radio, October 1989) |
Transmission lines have many applicatons in the fields of radio and telecommunications. In amateur radio, their most common application is in the coupling of energy between antenna and transmitter or receiver. Their performance is defined by various electrical characteristics and this article discusses the measurement of some of these characteristics.
Introduction
The theory of transmission lines is introduced in most amateur radio handbooks and it is not proposed to iterate on all that theory here. For our purposes, it is sufficient to introduce some of the most important constants and characteristics such as the electrical line constants, characteristic impedance, attenuation per unit length and velocity factor with an aim to discuss how these constants and characteristics can be measured.
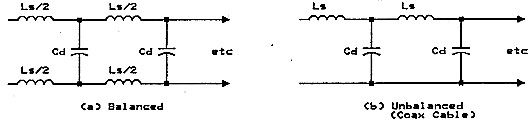
Transmission lines can be balanced (eg: open wire lines) or unbalanced (eg: coaxial cable). The constants, characteristics and measurements, discussed in the following text, apply to both types of lines.
Of most interest to the radio amateur are short transmission lines which connect a transmitter or a receiver to an antenna. The need to determine characteristic impedance often arises with that length of unknown coaxial cable bought at the amateur radio buy and sell mart. Velocity factor is needed when cutting that matching stub or phasing those driven elements on that antenna array. The need to measure attenuation arises when that length of coax is getting old and deterioraton of its performance is suspected.
Characteristic Impedance
Characteristic impedance of a transmission line is the value of impedance presented at its input when it is an infinite length. For a finite length of line, the same impedance is presented at its input if its output is terminated in an impedance equal to the characteristic impedance. When terminated in that impedance, all the energy sent down the line is absorbed by the terminal load and no energy is reflected.
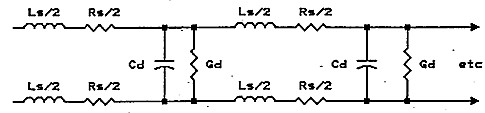
The transmission line can be considered to be made up of four electrical constants:
Ls - series inductance per unit length
Rs - series resistance per unit length
Cd - shunt capacitance per unit length
Gd - shunt conductance per unit length
An electrical representation is shown in figure 1. Constant Rs results from the AC resistance of the conductors. Gd is the reciprocal of the loss resistance in the dielectric between the conductors.
Characteristic impedance (Zo) is calculated from the line constants as follows:
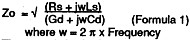
The term jwLs is the series inductive reactance per unit length (Xs) and the term jwCd is the reciprocal of the shunt capacitive reactance (i.e. susceptance) per unit length (Bd). At low frequencies, variation in the relative values of these terms to Rs and Gd results in Zo becoming larger as the frequency is decreased.
At high frequencies. jwLs is large compared to Rs and jwCd is large compared to Gd. Hence, at high frequencies, calculaton of characteristic impedance is simplified to the following:
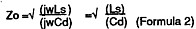
This formula is the one commonly found in radio handbooks. The simplified electrical representation in this form is shown in figure 2. Because the values of inductance (Ls) and capacitance (Cd) are independent of frequency, Zo is constant at high frequencies.
Characteristic impedance of a finite length of line at a given frequency can be derived by taking two impedance measurements, one with the end open circuit and the other with the end short circuited. From these, Zo is calculated as follows:

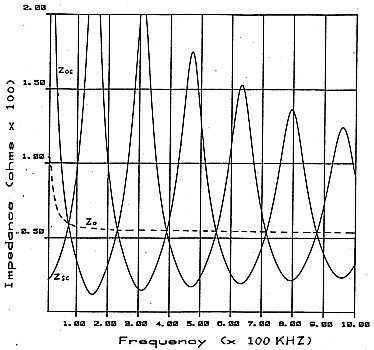
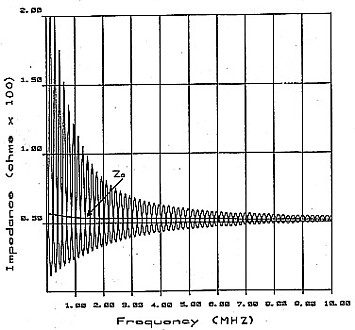
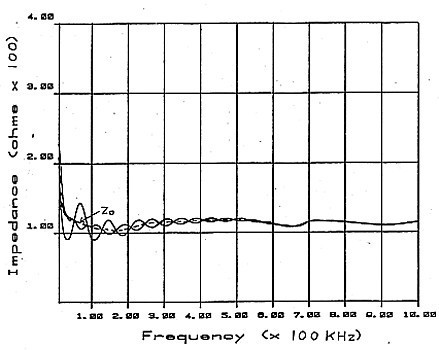
Figure 3 shows open circuit and short circuit impedance measurements carried out on 300 metres of RG122U 50 ohm coaxial cable over a frequency range of 1 kHz to 100 kHz. The calculated Zo has been added and this illustrates the rise in the value of Zo at low frequencies and the near constant value of Zo, just above 50 ohms, at high frequencies. Figure 4 shows the same cable plotted from 10 kHz to 1 MHz. Observe how the Zo line can be drawn through all the intersection points of Zoc and Zsc. Figure 5 extends the frequency even further with a plot from 100 kHz to 10 MHz. It can be seen that as the frequency is made higher, the excursion of Zoc and Zsc from the value of Zo becomes less, approaching nearer to the condition of an infinite line. The effect would be the same if the frequency were held constant and the length of line gradually increased.

|
 |
|
1 kHz to 100 kHz |
10 kHz to 1 MHz. |
In figure 6, the same type of measurements have been carried out on a one Kilometre length of telecommunications type twisted pair, over a frequency range of 100 Hz to 10 kHz. For this length of line, Zsc can be seen to be fairly constant at low frequencies, defined essentially by the DC resistance of the cable. On the other hand, Zoc rises rapidly as the frequency is decreased and the reactance of Cd rises. The characteristic impedance of this type of cable is nominally around 130 ohms at high frequencies, but in the voice frequency range, its impedance is in the region of 500 to 1000 ohms. This explains why a twisted pair is considered as a 600 ohm circuit in our voice frequency telephone system.
 |
 |
|
|
|
The open circuit and short circuit measurements can be made with a direct reading impedance analyser, or if the instrument gives a result in terms of reactance (X) and resistance (R), impedance (Z) is derived from:
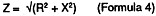
Most impedance measuring devices are unbalanced and difficulties can arise in measuring long balanced lines with these instruments. Figure 7 shows a measurement made on our one kilometre length of twisted pair using an unbalanced instrument and plotting over a frequency range of 10 kHz to 1 MHz. The high frequency impedance stabilises around 130 ohms but there are perturbations shown in the curve. These were caused by interference to the measuring device from unbalanced signal components picked up from local broadcast stations and aircraft homer beacons. The interference can be eliminated by using a coupling transformer between the instrument and the line but the characteristics of the transformer must be taken into account in interpreting the results of the measurement.
A simple method to measure open circuit and short circuit impedance is shown in figure 8. A signal generator is fed via resistance Rs into the line load or substitution resistor Rx, as selected by switch Sw. Rs is made high to simulate a constant current source. Assuming constant current, voltage across the line or resistor load is directly proportional to the impedance of the load. Sw is first selected to connect the cable with its end open circuit. Voltage fed to line is measured using a cathode ray oscilloscope (CRO) or a vacuum tube volt meter (VTVM) coupled through a high impedance probe. The switch is then operated to connect variable resistor Rx which is adjusted to obtain the same voltage. The resistance value of Rx is now equal to the open circuit impedance and if Rx is uncalibrated, its value can be measured using a multimeter or resistance bridge. The procedure is then repeated with the end of the cable short circuited to obtain short circuit impedance.
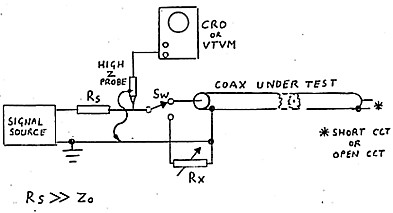
To achieve good accuracy in measurement, source resistance Rs should be made as high as possible and at least several kilo-ohms. However, if made too high, there could be some difficulty in getting enough voltage for a workable reading on the CRO or VTVM. Using equipment in the writer's radio shack, a value of 2.2 k ohms was as high as could be tolerated for a suitable CRO reading. With this value of Rs, characteristic impedance of three cables, believed to be 50, 75 and 95 ohms respectively, measured 54, 78 and 99 ohms. These measurements were a little high but near enough to identify which cable was which.
In measuring the high frequency characteristic impedance by this substitution method, a precise value of measurement frequency is not important. However, a frequency as low as 1 or 2 MHz is suggested so that the capacitance and inductance of the high impedance probe and connecting earth lead, have little effect on the measurement accuracy.
Use of the Line Constants
Another method of determining characteristic impedance is to measure the line constants and calculate impedance from these. To measure the constants, a length of cable must be cut no greater than one eighth of a wavelength at the frequency of measurement or, if the cable length is fixed, the frequency of measurement must be lowered until this criterion is achieved. With the cable end short circuited, values of series inductance (Ls) and series resistance (Rs) are measured. With the cable end open circuit, values of shunt capacitance (Cd) and shunt conductance (Gd) are measured. In practical cables, shunt resistance is high and Gd can generally be ignored and considered as equal to zero. Using the values measured, the characteristic Impedance can be calculated either from formula (1) or, for high frequencies from formula (2). There is one factor to be considered when making use of the series resistance constant (Rs). Due to skin effect the series resistance increases with frequency and hence the value of Rs can only be considered valid if measured near the frequency at which the impedance calculation is made. At high frequencies, formula (2) is used and variation in the value of Rs is of no consequence.
As a practical example, the 300 metre length of RG122/U was measured using this method to satisfy the less than one eighth wavelength criterion, the constants were measured at 20 kHz. Results were as follows:
Short circuit
Ls = 87.8 microhenries (Xs = 11.3 Ohms)
Rs = 21.5 Ohms
Open circuit
Cd = 29.53 nanofarad (Bd = 3.7 millimhos)
Gd = 0.097 millimhos
At high frequencies, the square root of Ls/Cd calculates to 54.5 ohms and close to that derived in the curve of figure 4. At the measuring frequency of 20 kHz, the complex quantities calculate to give Zo = 80.7 ohms. For those unfamiliar with complex numbers and "J" notation, where you see a term such as "R + jX" simply calculate impedance (or admittance) using the square root of the sum of the squares, as in Formula 4.
Any instrument which can separately measure resistive and reactive components can be used to measure the line constants. A Q meter can be used but measurement must be carried out at frequencies in the megahertz region with a much shorter length of cable than that of the previous example. If the cable length were reduced by an order of 300 to 1 metre, the line constants could be expected to be changed by the same order and Ls would equal 0.3 microhenry and Cd would equal 98 picofarad. The Q meter could comfortably handle these values. Increasing frequency by the same order would give a suitable measuring frequency of 6 MHz.
The line constants can also be used to calculate other characteristics of the cable such as attenuation, phase velocity and dielectric constant. Attenuation is frequency dependent because of the variation in series resistance (Rs) and shunt conductance (Cd), both of which increase in value as the frequency is increased. Phase velocity and dielectric constant are only dependent on Inductance (Ls) and capacitance (Cd) and hence their values are constant, independent of frequency. More detail on how to calculate the value of these characteristics from the line constants is given in the appendix at the end of the article.
Pulse Echo Testing
One way to determine the time taken for a signal to pass down a length of transmission line is to feed, into the line, short duration pulses separated in time by a value greater than the expected transmission time. The time taken for a pulse to get to the end of the line, or to be returned after reflection, is measured using the calibrated time base and graticule of a cathode ray oscilloscope (CRO).
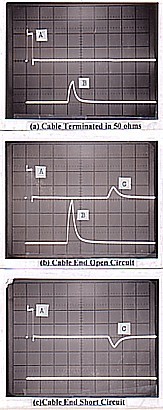 |
Figure 9 Pulse Echo Tests on 300 metres of RG122U 50 ohm cable. A = incident pulse; B = received pulse; C = pulse reflected back to input. Time scale is 500 nanoseconds/division. |
Figure 9 is a record of some tests carried out on the 300 metres of RG122/U ohm cable to determine transmission time over its length and hence its velocity factor. In figure 9 (a), the 250 nanosecond pulse A on the top trace is fed down the cable which is terminated in 50 ohms at the other end. Pulse B on the second trace is the signal received at the terminated end and displaced in time by 1.5 microseconds. The transmission time for 300 metres of cable is therefore 1.5 microseconds.
In figure 9 (b), the termination is removed so that the end is open circuit. The signal is now reflected back to the input and is shown as pulse C displaced 3 microseconds from the initiating pulse A. The pulse amplitude of B at the open end has noticeably increased in level but there is no need to consider this pulse at all as it is only necessary to halve the time between C and A to obtain the cable transmission time.
In figure 9 (c), a short circuit is placed across the cable end. Again, the pulse is reflected back to the input 3 microseconds later. It can be seen that the reflected pulse C is now inverted and this is because a reflection from a short circuit, or a lower resistance than Zo, produces a phase reversal. If "t" is the time recorded between pulses C and A and "S" is the length of the cable, velocity factor (V), or the ratio of phase velocity in the cable to that in space, is calculated as follows:
V = S/(150t)
= 300/(150 x 3) = 0.67
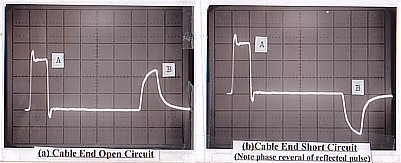
In f igure 10, we set out on a different tack to measure the unknown length of a roll of RG58 cable which we know has a velocity factor of 0.66. In this case, we have used a pulse width of 200 nanoseconds and the time measured between incident pulse (A) and reflected pulse (B) is recorded as 0.65 microsecond. The length (S) is calculated as follows:
S = 150tV
= 150 x 0.65 x 0.66 = 64.4 metres
The pulse echo measuring technique can also be used to locate faults in a transmission line. Any discontinuity in the impedance of a line will cause a reflection of signal. If the line develops a fault part way down the line, the location of the fault can be easily worked out in terms of distance to the fault by measuring time between the incident pulse and the pulse returned from the fault. The phase of the returned pulse also gives a lead to whether the fault might be an open circuit or a short circuit.
Pulse echo tests, such as those discussed, can easily be carried out using a simple pulse generator and a CRO with calibrated time base. The pulse duration is not critical but should be small compared to the transmission time measured. The higher the pulse repetition frequency, the easier it is to get a satisfactory CRO trace, but the time between pulses must be greater than twice the transmission time taken by a signal to pass down the line. In the tests recorded in figures 9 and 10, pulse spacing used was 5 microseconds.
As can be seen in figures 9 and 10, transmission within the cable degrades the rise time of the reflected pulse and to maintain accuracy of measurement, time should be measured between the leading edges of the initiating and reflected pulses.
The reflected pulse can be further used to determine characteristic impedance. The procedure is simply to substitute different values of terminating resistance until a value is found which returns no reflected signal. This value is equal to Zo. The direction to increment or decrement the resistance value is indicated by whether the pulse is inverted or otherwise. A wide initiating pulse is recommended for this purpose as this gives a higher level of reflected pulse making it easier to obtain fine resolution of the precise resistance. Of course, the same substitution method of measuring Zo can be applied using a transmitter to feed a carrier into the line via an SWR meter to indicate lowest reflected power. In this case, one must be careful to minimise transmitter power to prevent burning out the substitution resistors.
A Simple Pulse Generator
A simple pulse generator for pulse echo measurements can easily be made using readily available integrated circuit packages. An example of such a generator, experimented with by the writer, is shown in figure 11. This is based on an idea found in one of the ETI circuit books and submitted to ETI by Philip Dennis. The pulse is generated by a monostable multivibrator N1 with pulse width controlled by the values of C2, R3 and RV1. The circuit is arranged to re-trigger itself at a pulse repetition time set by the values of Cl, R2 and RV2. Using the circuit values shown, pulse width is adjustable between 50 and 500 nanoseconds and pulse repetition time is adjustable between 0.5 and 10 microseconds. A non locking start switch or button SW1 was found to be a necessary inclusion in the circuit as the pulse train did not always start itself on power up. Emitter Follower V1 provides a low source resistance to feed the test cable.
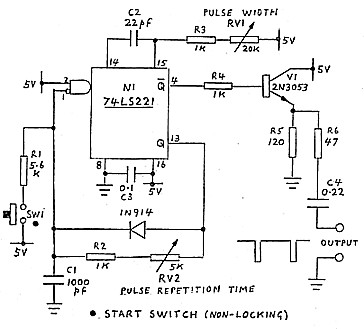
The Q bar negative going pulse output is used as this gives a better shaped output waveform than the positive going output which is loaded by the pulse repetition timing circuit. For the purposes of the transmission line tests, it does not matter whether the pulse is positive going or negative going but if desired, the whole circuit could be inverted by reversing the connections on the input AND gate, reversing the diode and reversing the Q and Q bar connections. Another alternative would be to add an inverter gate between the Q bar output and the follower stage.
Measurement Using Current Nodes
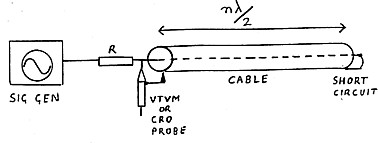
If the end of a transmission line is short circuited, a current node occurs at a half wavelength (and any subsequent half wavelengths) from the shorted end. This can be used to measure the velocity factor of a line or cable as shown in figure 12. For this test, a signal generator is fed via a resistor to one end of the cable and the other end is a short circuit. A high impedance probe from a VTVM or a CRO is connected right at the signal source end. The frequency of the signal generator is adjusted for a dip in voltage reading on the VTVM or CRO indicating a current node. Using this frequency in the calculation, velocity factor is derived as follows:
Velocity factor (V) = Sf/150n
Where S = length of cable in metres
f = frequency (MHz)
n = number of half wavelengths
("n" is any integer which gives a value of V between 0.5 and l.)
Attenuation
Attenuation of a transmission line can be measured by a number of methods. If the line is correctly terminated in a resistance equal to its characteristic impedance, a signal can be sent down the line and the voltage across its termination can be compared with the voltage fed into the cable. The signal source can be a signal generator or a transmitter and the voltage can be monitored on a VTVM or a CRO via a high impedance probe. Attenuation in dB is equal to 20 times the logarithm of the voltage ratio. Test probes normally have a capacitance of 10 pF and this capacitance, together with the inductance of the probe tip and earthing conductor, will upset the matching at VHF frequencies. Hence, this method of measurement is not recommended above 25 MHz.
Most radio amateurs have a coaxial line swr/power meter and this can be used to compare power at each end of the cable. The cable is again terminated in a resistance equal to its characteristic impedanance, the usual dummy load. The meter is first inserted at the transmitter end and the transmitter power, or the meter adjustment, is set for a full scale reading of power (say 10 on the meter scale). Being careful not to alter the transmitter and meter adjustments, transfer the meter to the load end and read off relative power. For example, if the scale reads 7, the power ratio is 7/10 = 0.7 and the cable attenuation is minus 10 times the logarithm of this value (i.e. 1.55 dB). Attenuation per unit length is calculated by multiplying the measured attenuation by the ratio of unit length to length measured.
A method of checking the attenuation of coaxial cable, using a SWR meter at one end, has been described in some issues of the ARRL antenna handbook, and was also described in Novice Notes, AR December 1978. In this method, a short circuit is connected at the load end of the cable and SWR is measured at the transmitter or source end. The greater the attenuation, the lower the level of reflected signal and hence the lower the SWR reading. The decibel ratio of power returned to forward power, is a measure of cable attenuation times two, however the attenuation is greater than it would be if the cable were correctly matched. With the high SWR, higher current at current antinodes causes increased IR loss and higher voltage at voltage antinodes causes greater dielectric loss. Hence, a correction has to be made to derive expected attenuation when the cable is correctly matched. For further reading, Ron Cook VK3AFW has discussed this effect in Novice Notes, AR November 1981.
Curve A of figure 13, taken from the ARRL antenna handbook, shows the relationship between SWR at the transmitter and corrected attenuation for a cable when properly matched. This can be used to derive attenuation using the method described above with the cable end short circuited. However, there are problems in the practical application of curve A. First of all, most SWR meters are only calibrated up to an SWR of 3 and even if they were calibrated higher, the upper scale graduation would be somewhat compressed. Using curve A, this somewhat limits attenuation measurements to 3 dB and above.
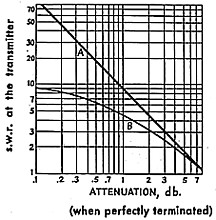
To obtain higher SWR measurements, the ratio reflected power to forward power can be directly measured. If your SWR meter does not have means to separately measure reflected power, what you can do is reverse the input and output connections to the meter and what is read as forward power will actually be reversed power. SWR is then calculated from the following:

A further suggestion is offered by the writer to resolve lower values of attenuation. To achieve this, we create a lower finite value of SWR at the load end of thecable. Curve B of figure 13 is a corrected curve for SWR at the transmitter verses matched attenuation when the SWR at the load is lowered to 10. This SWR can be achieved by terminating the cable in a resistance equal to one tenth of Zo. For example, use a 5 ohm termination for a 50 ohm cable. If the transmitter power is kept low, a number of carbon resistors in parallel can provide the termination. Applying curve B, low values of attenuation can be derived from lower and more readable, values of SWR than those obtainable using a short circuited cable.
Test Equipment
The extent to which the measurements discussed can be carried out in the radio shack depends on what test equipment is available. Some measurements can be carried out with the usual shack equipment of an SWR/power meter. Pulse Echo Testing requires the use of a CRO with calibrated time base and the use of a suitable pulse generator. If the CRO is uncalibrated, the time scale can be referenced against the signal waveform of a calibrated signal generator. If the generator is not accurately calibrated, this can be further referenced to a frequency counter, a Bendix type frequency meter, or a crystal marker generator. A pulse generator is hardly likely to be found in the shack but, as shown in figure 10, a simple one can easily be constructed.
Summary
A range of ideas have been presented on techniques which can be applied to the measurement of transmission lines. If suitable test equipment is available, an interesting day can be spent trying out some of these ideas and finding out all one can about those coax lines or other cables installed or stored away in the shack.
To finalise discussion, we repeat some of the salient points which have been presented:
The transmission line can be represented by four electrical line constants which, if measured, can be used to calculate characteristic impedance, attenuation, velocity factor and other characteristics.
Characteristic impedance is constant at high frequencies but rises inversely with frequency at very low frequencies.
Characteristic impedance can be derived by measuring separately the short circuit impedance and the open circuit impedance and calculating the square root of the product of these two measurements.
A pulse generator and calibrated CRO can be used to measure time between an incident pulse fed down the line and the reflected pulse returned from its end to derive either velocity factor or cable length when only one of these is known. The system can also be used to find the precise location of a cable fault and derive characteristic impedance using a load resistance substitution process.
Attenuation of a correctly matched line can be measured by direct comparison of voltage or power between the output and input of the line. It can also be derived by measuring SWR at the input of the line when the output is short circuited or terminated to give a known SWR at the load.
Appendix
