 |
INTRODUCTION
One of the factors which governs the performance of any amplifier system is the noise in the system. Noise might be defined as signals in the system which are unwanted and which degrade the desired signal content in the system.
As far as the amplifier system is concerned, noise can be divided into noise it receives at its input and noise it generates itself. A good system is one in which the noise generated by the amplifier itself is small compared to noise from the incoming source. In a HF receiver, for example, atmospheric noise is high and it is not difficult to achieve this requirement. At VHF and UHF frequencies, atmospheric noise is low and performance is limited by the noise generated in the first stages of the radio receiver.
Noise is generated in all stages in amplifiers and radio receivers but it is the first stages, operating at the lowest signal levels, which are of main concern, particularly where low signals from aerials, microphones, etc, are to be amplified.
 |
THERMAL NOISE
There is no such a device as a perfect amplifier, but assuming such a device could be built, there is still a limit to how low a signal level can be detected. Figure 1 shows an amplifier fed from a signal source which has a resistance Rs . Thermal noise in the resistance generates a noise voltage (Et) as follows:
Et = 2√(KTBRs)
where K = Boltzmanns constant
T = Absolute temperature
B = Bandwidth in Hertz.
At normal temperatures (say 17°C), this simplifies to:-
Et = √(1.6 × 10-20 × BRs)
Short of fitting the source in a cryogenic chamber, this is the lowest noise which can be achieved at the amplifier input and the practical equivalent noise at the input is always higher than this.
EQUIVALENT NOISE VOLTAGE
Whilst noise generated by an amplifier system is generated within the system, the degree of noise is evaluated by referring it to the amplifier input, that is, it is considered as equivalent noise at the input as though it were being generated at that point. The equivalent noise voltage (En) is calculated by
dividing the noise measured at the amplifier output (Eno) by the gain of the amplifier (Av).
i.e. En = Eno/Av
BANDWIDTH
Noise in any system is dependent on bandwidth of the system and this must be specified when defining noise performance. It is common practice to define noise for a 1 Hz bandwidth, for example, noise voltage might be specified in nanovolts per square root of Hertz (nV/√Hz). Over a limited bandwidth, noise power can be considered to be proportional to bandwidth and noise voltage proportional to the square root of bandwidth. If noise voltage is defined for a 1Hz bandwidth system, noise can be determined by multiplying by the square root of the system bandwidth.
The level of noise generated by an amplifier system generally varies over a wide spectrum and for a wide bandwidth, the noise performance must be defined by plotting noise (say in nV/√Hz) against frequency.
EQUIVALENT NOISE VOLTAGE AND CURRENT GENERATOR
In considering solid state amplifiers, noise is often resolved into two components at the amplifier input, an equivalent noise voltage generator (Vn) and an equivalent noise current generator (In) (refer figure 2). The first component (Vn) is independent of the value of source resistance (Rs). The second component (In) develops a noise voltage across Rs equal to InRs, that is, the noise voltage it develops is directly proportional to the value of Rs.
 |
Vn can be separated from the voltage developed by In and also the thermal noise (Et) by short circuiting the input terminals. The voltage developed by Et and In is then zero and what is left is the noise voltage generator Vn.
NOISE FIGURE
One method of defining the noise performance of an amplifier is the noise figure (F). This can be defined as the ratio of equivalent noise power developed at the input to that generated by thermal noise in the source resistance (Rs). Noise figure is often expressed in decibel form. A perfect amplifier would have a noise figure of 0dB, if such a device were possible.
To establish noise figure, the voltage gain (Av) of the amplifier is measured and the noise voltage output (Eno) is measured at a known bandwidth (B). For the second measurement, the amplifier input must be terminated in a resistance (Rs) equal to the normal source resistance. Noise figure is calculated as follows:
F = 20 log{Eno÷ [Av√(1.6 × 10-20 × B × Rs)]} dB
Figure 2 and the formula assumes a high impedance input to the amplifier. The effective value of Rs as far as the calculation is concerned, is the parallel result of the source resistance and input resistance of the amplifier. If the source is a transmission line and it is terminated in its characteristic impedance (Zo), then Rs should be substituted by a value Zo divided by 2.
TRANSISTOR NOISE
The value (Vn) of the equivalent noise voltage generator in a bi-polar transistor can be calculated from the following formula:
Vn = 0.0147/√Ie nV/√HZ
where Ie = Emitter current in amps.
Note that the noise voltage is entirely dependent on emitter current and decreases as the emitter current is increased.
Derivation of the value of the equivalent noise current generator is more complicated. Its value is dependent on various constants which vary with transistor type and which also vary between selected samples of the same type. For lowest noise, it is therefore necessary to select samples on a test basis. The noise current is also dependent on emitter current and frequency. Figure 3 illustrates a typical change in noise current with frequency for a bi-polar transistor, giving a rise in noise current below 1000 Hz. Above 1000 Hz, noise current is constant.
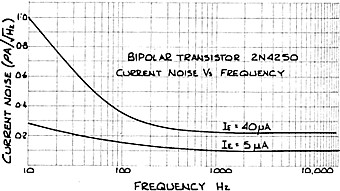 |
In contrast to the value of the noise voltage generator, the noise current value increases as emitter current is increased. The noise voltage developed from the noise current is further dependent on the value of source resistance (Rs) through which it flows. (Refer previous paragraphs).
In consequence, for a given transistor, at a given frequency, there is an optimum emitter current for each value of source resistance (Rs) used. This is a point on figure 4 at which the curve showing the noise voltage generator (negative slope) intersects with that of the appropriate curve (for Rs) showing noise voltage derived from the noise current generator (positive slope).
 |
At low values of source resistance (say 50Ω), the equivalent noise voltage generator is the dominate factor and lowest noise is achieved at emitter currents in the order of several milliamps. At higher source resistance, (0.1 to 1MΩ), noise voltage developed from the noise current is dominant and emitter currents in the micro-amp region must be used to reduce the noise. (It is also of note that if common emitter configuration is used, these low emitter currents are necessary to achieve the high input resistance required).
For a low source resistance, a low noise bi-polar transistor works well and provides high gain. A typical noise current is 0.1 pA/√Hz and of little consequence developed across the low source resistance. For a high source resistance, a low noise field effect transistor is more suitable. Noise current at the input of a field effect transistor is a fraction of that for a bi-polar transistor and even at high impedances, the equivalent noise voltage generator is the dominant factor. For low noise, drain current in the order of 2 to 10 mA is used.
Field effect transistors have found quite universal use as low noise front end amplifiers in VHF and UHF receivers where their gate is connected across the high impedance input of a tuned circuit.
A TYPICAL NOISE PROBLEM
One typical noise problem occurs when a piezo electric device (such as a microphone) is used at audio frequencies and connected to the input of an amplifier. At audio frequencies the device can be considered as a generator in series with a small capacitance (refer figure 5). Supposing the series capacitance were 4 nF and frequency response down to 10 Hz were required; the device must then be terminated in not less than 20 MΩ to achieve response at the low frequencies. Referring again to figure 5, it can be shown that such an example places a resistive component across the amplifier input of 0.8 MΩ at 10 Hz compared with 80 Ω at 1000 Hz. The high equivalent source resistance at the low frequencies is a problem where amplifier current noise develops a noise voltage across that resistance. Quite apart from amplifier noise, the high value of Rs puts a limit on the lowest noise voltage achievable due to factor KTBRs.
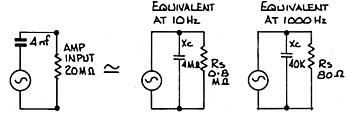 |
Bearing in mind the problem discussed in the previous paragraph, the writer tested a number of different operational amplifiers and discrete transistor circuits to compare noise at the input using the 4 nF and 20 MΩ example. Table 1 shows the results obtained.
Discrete bi-polar transistors running at very low collector currents demonstrated a lower noise voltage than the operational amplifiers tested. At low frequencies, where the value of Rs is high, the FET gave the best performance, At higher frequencies, where the value of Rs is low, the bi-polar and FET transistors are comparable. Had the bi-polar transistors been run at milliamps of collector current instead of microamps, they would have out-performed the FET transistors at the higher frequencies but been unsatisfactory at the low frequencies where Rs is high.
One interesting device (not included in the Table 1 tests), is the Burr-Brown OPA111 FET operational amplifier. According to the curves published for this device, it would produce noise figures comparable with the discrete FET transistors tested. (At 10 Hz with an Rs = 1 MΩ, noise voltage would be 120 nV/√Hz. At 1000 Hz with an Rs = 100 Ω, noise voltage would be 7nV/√Hz).
| Device | Rs = 0.8 MΩ F = 10 Hz | Rs = 80 Ω F = 1000 Hz |
| OP AMP OP7 | 773 | 18 |
| OP AMP OP5 | 2711 | 18.5 |
| OP AMP NE5534A | 7553 | 18 |
| OP AMP ADS10 | 782 | 29 |
| OP AMP LM11 | 330 | 256 |
| OP AMP LA3140 | 262 | 45 |
| OP AMP AD504 | 3374 | 19 |
| OP AMP BB3510 | 1919 | 21 |
| OP AMP LM308 | 256 | 32 |
| OP AMP μA776 | 1211 | 38 |
| Balanced bi-polar transistors 2N4250 (Ic = 2 x 9μA) | 450 | 8 |
| Balanced bi-polar transistors 2N4250 (Ic = 2 x 3μA) | 207 | 15 |
| Balanced FET transistors 2N5523 (Id = 2 x 1mA) | 130 | 6 |
| Thermal noise limit [2√(KTBRs)] | 126 | 1.3 |
MEASUREMENT OF NOISE
To measure equivalent noise voltage at an amplifier input or to measure noise figure the following is required:
(1) A means to measure RMS noise voltage over a controlled bandwidth,
(2) A means to measure the voltage gain of the amplifier.
Voltage gain can be measured using a signal generator and calibrated CRO suitable for the frequency spectrum of interest. A spectrum analyser is very useful to measure noise voltage as it usually has a defined bandwidth or means to adjust bandwidth over which the measurement is made. (Refer figure 6).
Equivalent noise (En) in nV/√Hertz is calculated from the measurements as follows:
En = Eno.109 ÷ (Av√B)
where Eno = Measured noise output voltage
Av = Amplifier voltage gain
B = Bandwidth of measurement in Hertz.
 |
THE NOISE DIODE
One means used to measure noise figure in the VHF and lower UHF region is to use the thermionic noise diode (refer figure 7). Plate current is fed through resistance Rs which becomes the source resistance of the noise generator formed. The plate current is controlled by varying the filament voltage of the diode. It turns out that for a temperature limited diode, the noise component of the plate current is precisely related to the DC plate current as follows:
If the plate current is adjusted so that the noise power in the receiver being tested is double that for zero plate current, then noise figure (F) = 0.02 I.Rs,
where I = the plate current in milliamps.
For a source (Rs) = 50Ω, the formula is simply F = I, hence the noise figure can be read directly from the plate current value.
Equivalent input noise power for the receiver is KTBI and the equivalent input noise voltage (En) is:
En = √(1.6 × 10-20 × I × Rs)
V/√Hz
 |
Many years have passed since solid state electronics phased out most uses of the vacuum tube and hence suitable tungsten filament diodes are not easy to obtain. An alternative noise generator can be made using a semiconductor diode (refer figure 8). In this case, the relationship between noise voltage and diode current will depend on the characteristics of the diode and for the device to be of any use in testing receiver performance, it must be calibrated against a known noise source.
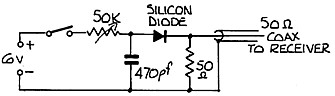 |
Noise power change is best measured at the output of the IF amplifier in the receiver. In an AM receiver (but not an FM receiver), audio noise power can be measured. The method is to gradually increase the diode current until the power indication is double, or if an AC voltmeter is used, until the voltage increases by a factor of 1.4. (Refer also to figure 9).
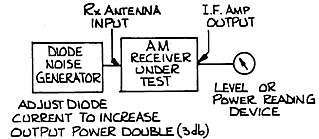 |
RADIO RECEIVER PERFORMANCE
A discussion on noise would not be complete without reference to specifications for receiver performance since such specifications are tied to amount of noise generated in the first stages of the receiver.
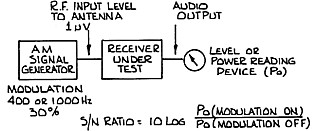
Amplitude Modulation (AM) receivers are often given a signal to noise ratio for a given input level in microvolts, e.g. 15 dB S/N ratio for 1μV of signal. What is assumed (if not quoted) is that noise power at the audio output is 15 dB below a 400 Hz or 1000 Hz signal demodulated from a 30% modulated, 1 μV signal at the receiver input. To get some idea of noise performance, the receiver bandwidth must also be considered. A 15 dB S/N ratio for a 3 kHz bandwidth receiver is not as good a noise performance. as one with a 15 dB S/N ratio with 6 kHz bandwidth.
A single sideband receiver might be quoted as 12 dB S/N ratio for 1 μV of sideband. This implies noise 12 dB below 1 μV, i.e. 250 nV. If the receiver has a bandwidth of 3 kHz and its input resistance is 50 Ω, thermal noise is calculated as 49 nV and noise figure is 20 log(250/49) = 14 dB.
The noise performance of a Frequency Modulation (FM) receiver is more difficult to define. Noise, as has been considered, is caused by random amplitude variation which the FM demodulator is designed to reject. The noise takes dominance when the FM signal level falls to a critical level and it has been a practice to quote decibels of quieting for a given input signal level, e.g. 20 dB of quieting for 0.5 μV. Whilst this gives an indication of the noise performance of the front end of the receiver it does not give assessment of the noise performance as an FM detector and an additional specification giving decibels of S/N ratio for an input signal deviated by a fixed amount is also required, e.g. 20 dB S/N ratio for 0.3 μV signal deviated 5 kHz by 1000 Hz tone.
A more recent specification is SINAD performance. For this, a minimum signal input level in microvolts is given which satisfies a given level (12 dB) of noise and distortion below a modulating tone (1000 Hz deviating 3 kHz in a 5 kHz maximum deviation system). To test a receiver, an FM signal generator, modulated by a 1000 Hz tone to a deviation of 3 kHz, is fed to the aerial input and the audio output is monitored with a distortion meter (refer figure 11). The input level is decreased until distortion read is 25% (i.e. 12 dB of noise and distortion below the tone level).
The difference between SINAD measurement and previous methods of measurement is that the tone is tuned out at the output of the receiver instead of switching off at the input signal source. With tone removed, noise components remain and in the SINAD case, include distortion components generated in the receiver by the tone itself.
A conventional method of measuring signal to noise ratio in an AM receiver is illustrated in figure 10. Performance testing of an FM receiver using the SINAD method is illustrated in figure 11.
 |
 |
SUMMARY
Low equivalent noise at the input is better achieved using discrete transistors with controlled collector (or drain) current rather than IC packages. Bi-polar transistors are good for a low source resistance but FET transistors perform better for high source resistance.
Noise can be measured by a number of methods which have been described.
At VHF the noise diode is useful to measure noise performance.
Assessment of the noise performance of FM receivers requires different test procedures to those for AM receivers.