Apparent variable area of a triangle by VK3UKF
2006.
Please do not make comment on this without having tried it
out first. Unless you're sure !
About 2
years ago, (2004) an aquaintance passed only the image on this page, on to me.
No explanation.
----------------------------------------------------------------
After
you have made the appropriate shapes out of either paper (from printing the
image out), or plywood or hardboard that fits into a recessed cutout of the same
dimensions. (Like a child's jigsaw puzzle that has 4 pieces.)
You will, no
doubt, feel exhilaration as you discover that you can actually do it, and it
works repeatedly.
You will want to run and show your friends this new
discovery.
Then you will try to figure it out.
You will fail.
You
will then go slightly crazy or mad.
You may even be compelled to hold your
head and sob.
You will then feel pain as logic escapes you totally.
I will save you.
The answer is to actually show it to your
friends, and watch them as they experience and display exactly what you just
did.
----------------------------------------------------------------
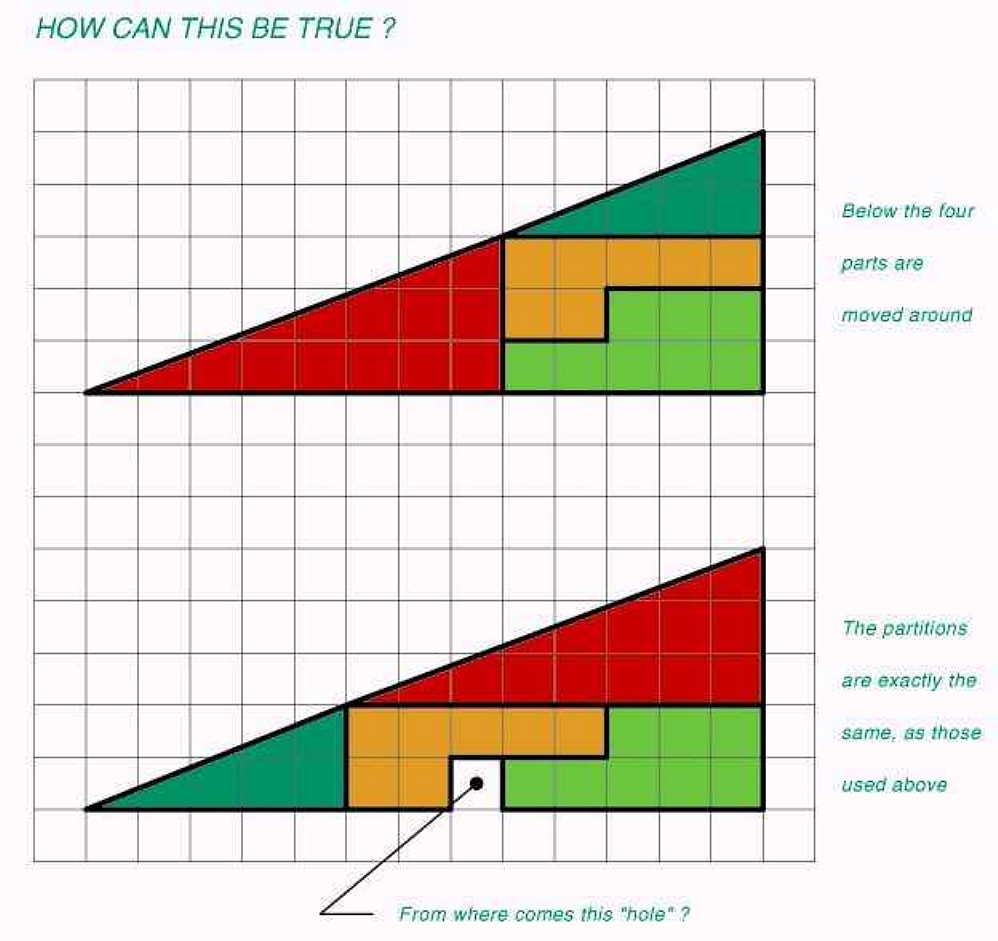
Using the dimensions shown in the image above, the area of a triangle is
apparently variable.
The possibilities as to the utilisation of this
information boggle the imagination.
Real-estate sub-divisions tend to come
to mind straight away.
To save the image, right click, then click 'save
target as'. File size 72 kb.
----------------------------------------------------------------
IT
JUST DOESN'T ADD UP !
----------------------------------------------------------------
THE
MAIN TRIANGLE
The base is 13 units in length.
The vertical side
forming the right angle with the base is 5 units in height.
The length of
the hypotenuse opposite the right angle is the sqr root of (13 sqrd (169) + 5
sqrd (25) = 194) = 13.92838828 units. The angles either side of the hypotenuse
are
Tangent of theta is 5/13 = 0.384615384. Arctangent of 0.384615384 is
21.037511 degrees,
therefore the other angle is 90 - 21.037511 = 68.962489
degrees.
THE SMALL GREEN TRIANGLE
The base is 5 units in length.
The vertical side forming the right angle with the base is 2 units in
height.
The length of the hypotenuse opposite the right angle is the sqr
root of (5 sqrd (25) + 2 sqrd (4) = 29) = 5.385164807 units.
The angles
either side of the hypotenuse are
Tangent of theta is 2/5 = 0.4. Arctangent
of 0.4 is 21.80140949 degrees,
therefore the other angle is 90 - 21.80140949
= 68.19859051 degrees.
THE LARGE RED TRIANGLE
The base is 8 units
in length.
The vertical side forming the right angle with the base is 3
units in height.
The length of the hypotenuse opposite the right angle is
the sqr root of (8 sqrd (64) + 3 sqrd (9) = 73) = 8.544003745 units.
The
angles either side of the hypotenuse are
Tangent of theta is 3/8 = 0.375.
Arctangent of 0.375 is 20.55604522 degrees,
therefore the other angle is 90
- 20.55604522 = 69.44395478 degrees.
WHAT ???? Am I doing
wrong???, please let me know via email.
If you make a lot of money from
this, please don't forget me.
Thank you Sterling, I couldn't see the trees for the forest.
:-)
-----------------------------------------------------------------------------------------------------------------------------
As
explanations and comments arrive, I will place them here.
Answers supplied by Sterling K. Webb.
March 2006
Hi, Kevin,
Here's a fistful of answers to your puzzle:
http://mathforum.org/library/drmath/view/61087.html
http://www.nobeliefs.com/puzzles/triangle-puzzle.htm
(They want you to "contribute" before they tell you the answer...)
http://www.puzzle.dse.nl/harder/index_us.html#appearing_area
And here's the website your "friend" got the picture from,
only he didn't give you the answer, which is on the same website:
http://home.earthlink.net/~toddwolly/vision/triangle.html
Stop suffering...
Sterling K. Webb
----------------------------------------------------------------
Return to index.