HELL-O-WEEN
About the author
For questions about the Hell-o-Ween mode, contact me via mail.[1] For older photo’s and articles, click here[2].
Imaging with equations
Digital killed the Radio star
Outline and purpose
Hell schreiber , aka typerbildfeldfernschreiber, is an early facsimile-like mode to transmit text and images over the air. Unlike digital transmissions, this mode isn’t targeted for machine-to-machine communications ; It is a mode for humans to communicate and makes it a good mode for ham radio but also a low-level solution for a Web 3.0 human-centric Internet.
The code for this new hell-o-ween mode is explained step-by-step in the following sections:
First, the Hell schreiber mode is illustrated.
Then, Ghost imaging and Learning-with-errors is explained with a puzzle.
Then, python source code for a Helloween transceiver via audio and radio.
Have no fear…
We live in a challenging times - You see all kinds of challenges from TikTok to Youtube, so, I also want to share you a Hell Challenge
Can you decode the message in following images?
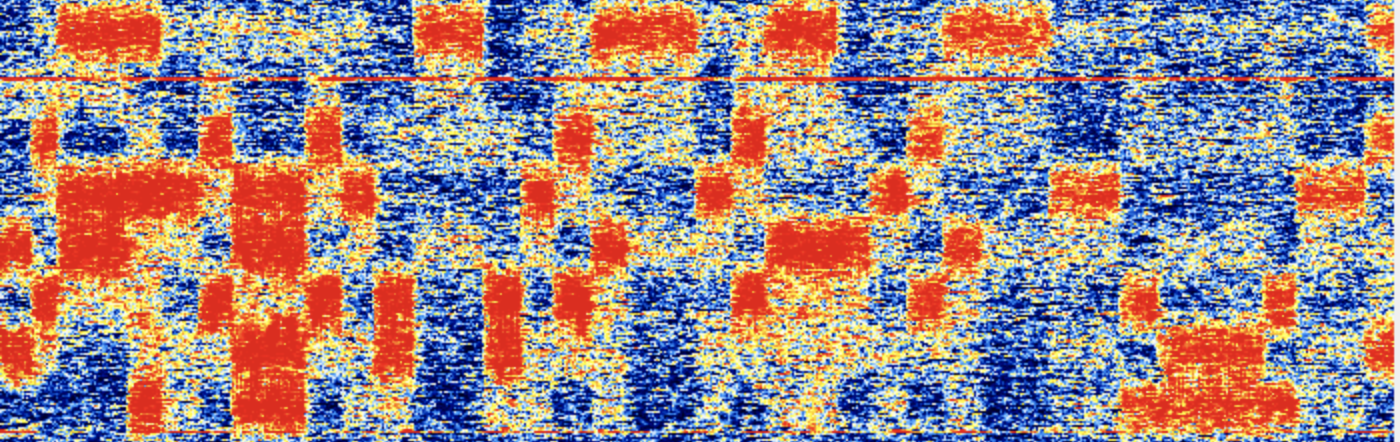
The puzzle was explained on a (Durch) Math forum and below in this text. Hint: The hidden message refers to a character from a book of Victor Hugo
Hell Schreiber
import sounddevice as sd
import numpy as np
msg="""
* * **** * * **
* * * * * * *
**** *** * * * *
* * * * * * *
* * **** **** **** **
""".split("\n")[::-1]
(amplitude, duration , samplerate) = ( 0.3, 5.5 , 44100.0 )
# carrier frequencies
tones= [ (300*(4+mi)) for mi in range(1,len(msg))]
def callback(indata, outdata, frames, time, status):
global sidx, idx, tones, amplitude
t = (sidx + np.arange(frames)) / samplerate
t = t.reshape(-1, 1)
# generate output
v = np.zeros(frames).reshape(-1,1)
for mi in range(len(msg)):
m = msg[ mi]
if m[idx%len(m)] == '*':
v = v + amplitude*np.sin(2 * np.pi * tones[mi] * t)
# decode input (microphone)
for tone in tones:
inv = indata * amplitude*np.cos(2 * np.pi * tone * t)
print "%6.2f;" % abs(np.sum(inv)),
outdata[:] = v
(sidx,idx) = (sidx+frames,idx+1)
(sidx,idx) = (0,0)
with sd.Stream(channels=1, callback=callback):
sd.sleep(int(duration * 1000))
Output
The hell schreiber image sounds like this.
The output as image looks like this:

Or, in as a waterfall:

Seeing ghosts….
Ghosts imaging is a technique to send and receive pictures without additional logic ; Raster-based television, like slow-scan-television (SSTV) uses a scanning beams and pixels, … but ghost imaging can be decoded with the human eye.[3]
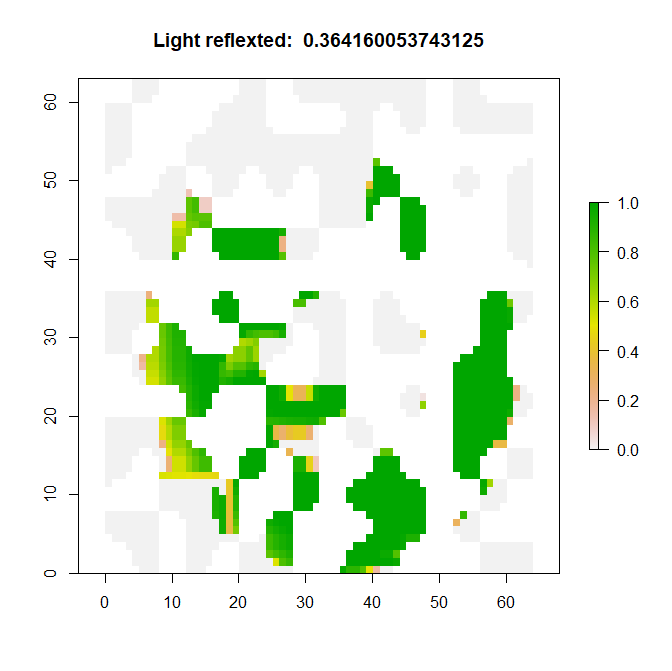
Here is how ghost imaging works (in R): Overlay a source image with a sequence of patterns (Xi) and observe the total amount of the reflected light (o_i). The steps of ghost imaging, programmed in R, are listed below:
|
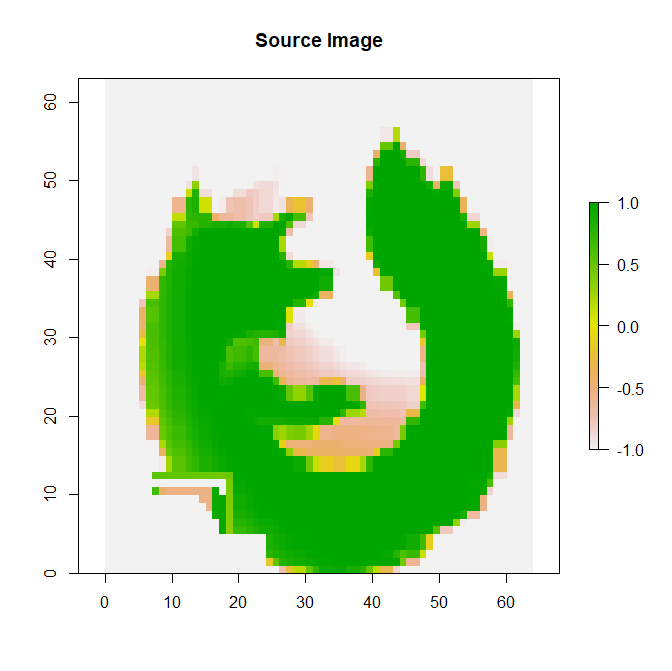
Original image (64.png) |
STEP 1 (a): Read in original image (‘grayscale’) |
|
|
|
|
STEP 1 (b): Hadamard matrix chosen at random |
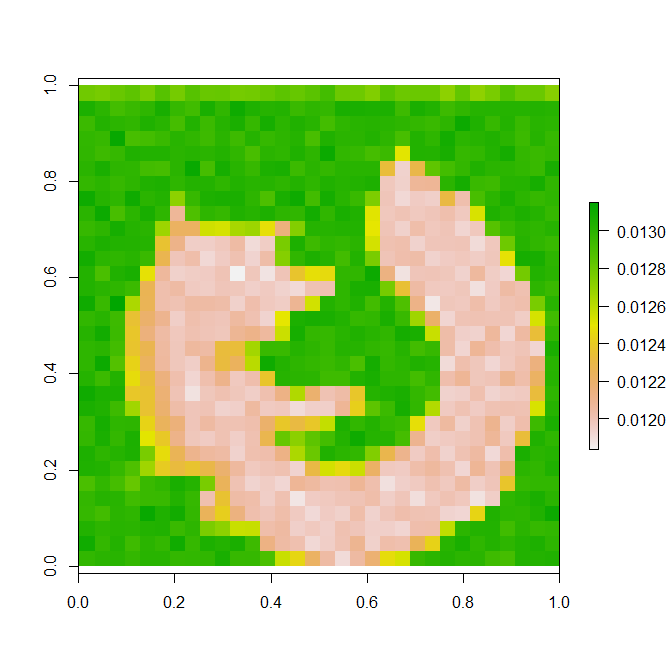
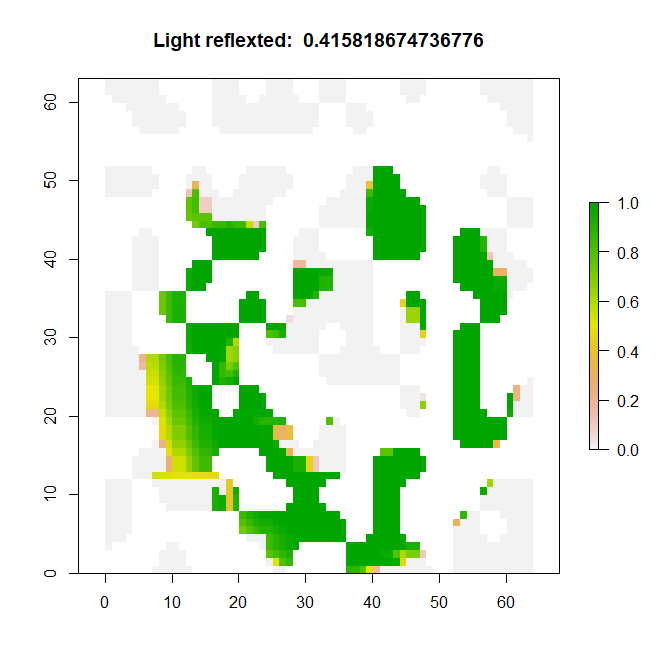
STEP n²: Image reconstructed after n² observations: |
|
|
|
In the process n² observations were used, each from a different Hadamard matrix: Shuffling a Hadamard results in another Hadamard image:
# in R:
h <- hadamard(hn)
pr = sample( hn )
pc = sample( hn )
hadamardshuffle = h[pr,pc]
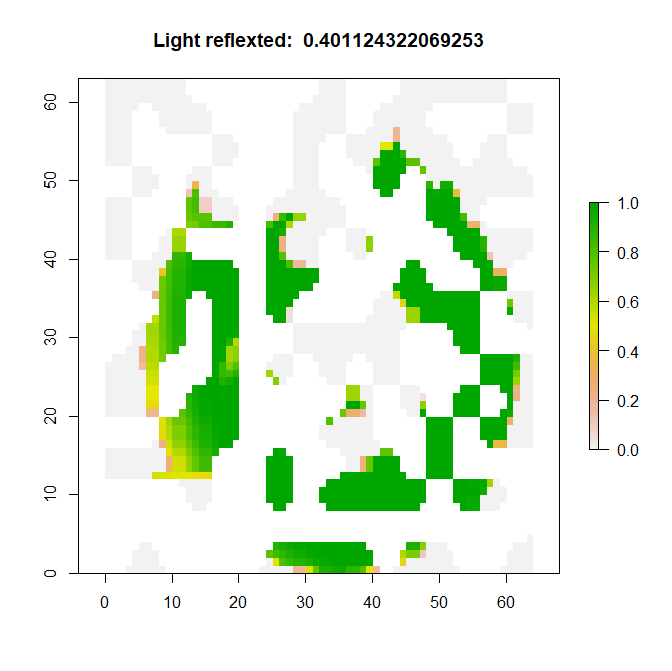
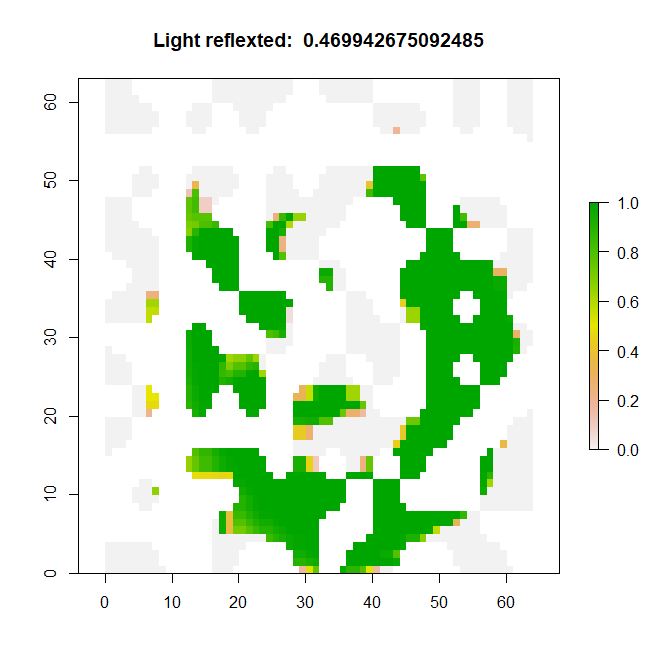
Here are some of the observations:
|
|
|
|
|
|
library(pracma)
library(raster)
require(gtools)
toghost <- function(h,s ) {
m <- raster( h ,xmx=64,ymx=64 )
mm <- resample( m,s, method='bilinear')
mm[mm >0 ] <- NA
ma <- mask(s,mm)
ma[ma <=0 ] <- 0
aa <- cellStats(ma, mean)
#DEBUG plot(ma,main=paste('overlayed image, reflection observed: ', aa ))
return( aa )
}
s<- raster( "64.png",band=1 )
s[] <- (s[]/255 - 0.5)*2 # hadamard values: [-1 .. 1]
hn = 32 # resolution, use 16 for lower resolution but faster
h <- hadamard(hn)
pr = sample( hn )
pc = sample( hn )
hshuffle = h[pr,pc]
a <- toghost(hshuffle,o )
o <- c(a)
X <- matrix()
X <- rbind( as.numeric( as.list(hshuffle) ))
for (i in 1:((hn2)-1)) {
pr = sample( hn )
pc = sample( hn )
hshuffle = h[pr,pc]
a <- toghost(hshuffle,s )
o <- c(o, a)
X <- rbind(X, as.numeric( as.list(hshuffle) ))
}
b = solve(X,o)
re <- matrix(b, nrow=hn)
plot(raster(re))
The equations for Hell-o-Ween in Excel
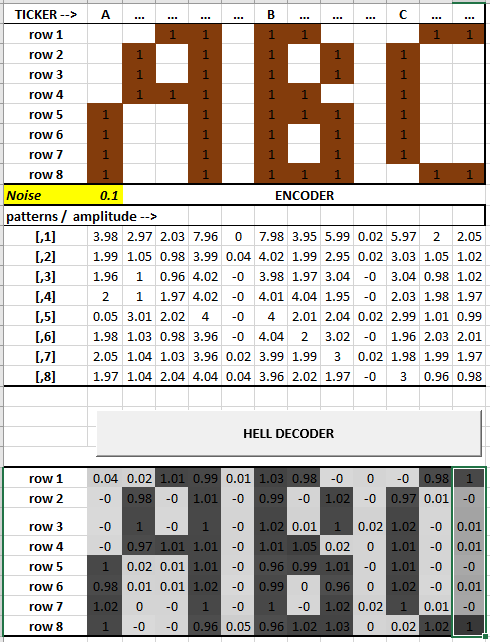
The ghost imaging technique can be applied to the Hell Schreiber ‘hell-o-ween’: The ghost imaging projects a number of overlay patterns on an image and observes each time the amount of reflected light. In the case of hellschreiber, the pattern and image is a simple 8x1 raster moving through time, like a ticker.
Download the excel workbook[4] to see the equations in a example.
|
Hell schreiber (without noise) |
Under noisy conditions … |
|
|
|
A Puzzle using Learning-with-errors
Learning with errors (LWE) as an encryption scheme it adds a ‘noise’ vector on a set of linear equation modulo ‘p’ (or, Si = HxMi + e mod p, and ‘p’ is 3 in our case). Retrieving the key ‘e’ through the noise should be very hard.
Encryption isn’t used in ham radio communications, but I’ve posted it as a puzzle on a Dutch mathematics forum (wiskundeforum.nl) on the 4th of September 2020 - see here. It was solved by ‘Arie’ on September 16th , 2020 by using the whitespace between the characters in the message.
The Ghost puzzle:
Let :
N, the length of a message
M, the message as 8xN matrix with Mi the i-the vector of that matrix (8x1)
S, the encoded ghost message as 8xN matrix with Si the i-the vector of that matrix (8x1)
And Si = ( HxMi + E mod 3 ) + noise
H, Hadamard matrix 8x8
E, an unknown vector 8x1
For example:
M is ‘HALLO’ ( Dutch translation ‘hello’ )
/ \
| 2 2 1221 2 2 1221 |
| 2 2 2 2 2 2 2 2 |
M = | 1111 2222 2 2 2 2 |
| 2 2 2 2 2 21 2 2 |
| 2 2 2 2 1222 1222 1221 |
| |
\ 21212122112221122112112211 /
With:
T
M1 = [ 0 2 2 1 2 2 0 2 ]
T
M2 = [ 0 0 0 1 0 0 0 1 ]
...
/ 1 1 1 1 1 1 1 1 \
| 1 0 1 0 1 0 1 0 |
| 1 1 0 0 1 1 0 0 |
| 1 0 0 1 1 0 0 1 |
H = | 1 1 1 1 0 0 0 0 |
| 1 0 1 0 0 1 0 1 |
| 1 1 0 0 0 0 1 1 |
\ 1 0 0 1 0 1 1 0 /
In the puzzle, the (noisy) image can be decoded as matrix S:
Helloween audio transmission
The script modulates and demodulates Helloween via a sound device. It outputs also a ‘CSV’ file with raw spectrogram values that you can visualize using the R script.
The quality of de communication depends heavily on the volume and noise.
Normal hellschreiber operation (n). Adjust gain for speaker output (a)
python hell.py na >hell.csv && Rscript hell-decode.R
Output image as linear equations in Ghost mode (g) ; It solve the equations via gauss (G).
- python hell.py gaG

Output image as linear equations in Ghost mode (g) ; It solve the equations via inverse modular matrix (X).
python hell.py gaMX
Output image as linear equations in ghost+lwe mode with key 0,1,1,1,0,1,1,0
python hell.py gmMXa "0,1,1,0,2,1,0,2"

Python source code
# device 2 is soundflower loopback audio device
#. without loopback, the quality isn’t very good for ghost mode
from __future__ import print_function
import sounddevice as sd
import math, sys
from numpy import matrix
from numpy import linalg
import numpy as np
from scipy.linalg import hadamard
from scipy.linalg import solve
def modMatInv(A,p): # Finds the inverse of matrix A mod p
n=len(A)
A=matrix(A)
adj=np.zeros(shape=(n,n))
for i in range(0,n):
for j in range(0,n):
adj[i][j]=((-1)**(i+j)*int(round(linalg.det(minor(A,j,i)))))%p
return (modInv(int(round(linalg.det(A))),p)*adj)%p
def modInv(a,p): # Finds the inverse of a mod p, if it exists
for i in range(1,p):
if (i*a)%p==1:
return i
raise ValueError(str(a)+" has no inverse mod "+str(p))
def minor(A,i,j): # Return matrix A with the ith row and jth column deleted
A=np.array(A)
minor=np.zeros(shape=(len(A)-1,len(A)-1))
p=0
for s in range(0,len(minor)):
if p==i:
p=p+1
q=0
for t in range(0,len(minor)):
if q==j:
q=q+1
minor[s][t]=A[p][q]
q=q+1
p=p+1
return minor
p = 3 # prime
e = np.array( [0,0,0,0, 0,0,0,0] )
mode = ""
try:
mode = sys.argv[1]
e = np.array( [float(ei) for ei in sys.argv[2].split(",") ] )
except IndexError:
pass
print("e:%s mode:%s" % (e , mode), file=sys.stderr)
#pmax = [1]*8
msg="""
* * **** * * ** * * **** **** * *
* * * * * * * * * * * ** *
**** *** * * * * * ** * *** ** * * *
* * * * * * * * ** * * * * * *
* * **** **** **** ** * * **** **** * **
* """.split("\n")[::-1]
h = ((1+hadamard(8))/2) % p
hinv = modMatInv( h, p )
pmax=[1]*8
( gain, threshold, duration , samplerate) = ( 0.125, 1, 10. , 44100.0 )
tones= [ float(300*(3+mi)) for mi in range(1,1+len(msg))]
def callback(indata, outdata, frames, time, status):
global sidx, idx, tones, amplitude, pmax, mode
t = (sidx + np.arange(frames)) / samplerate
t = t.reshape(-1, 1)
# generate output wave, from message column as vector 0,1,1,0,1,...
v = np.zeros(frames).reshape(-1,1)
if "D" not in mode:
col = np.array( [ 1 if msg[mi][idx%len(msg[mi])] == '*' else 0 for mi in range(len(msg)) ] )
if "g" in mode:
col = h.dot( col.T ) # do the ghost
if "m" in mode:
col = (col + e ) % p
for ci in range(len(col)):
carrier = col[ci]*np.sin(2 * np.pi * tones[ci] * t)
v = v + carrier
if "a" in mode:
outdata[:] = gain*v
else:
outdata[:] = v
# decode input data from microphone (tune to the tones)
b = np.array( [ abs( np.sum( indata * np.cos(2 * np.pi * tone * t))) for tone in tones ] )
if "M" in mode:
pmax=[ pmax[pi] if pmax[pi]>b[pi] else b[pi] for pi in range(len(pmax)) ]
b = ( p + ( (3*b)//(1+np.array(pmax)) ) ) % p
if "X" in mode:
b = ( hinv.dot( (b -e )%p ) ) % p
if "G" in mode:
b = solve( h, b )
print (";".join( [ "%6.2f" % abs(xx) for xx in b ] ))
(sidx,idx) = (sidx+frames,idx+1)
(sidx,idx) = (0,0)
with sd.Stream(channels=1, callback=callback , device=2 ): #, device=2 ): # device 2 is soundflower
sd.sleep(int(duration * 1000))
Visualization of hell-o-ween in ‘R’
library(pracma)
p=3
h = ((1+hadamard(8))/2) %% p
hinv = matrix(
c( 0.,1.,1.,1.,1.,1.,1.,1.,
1.,2.,1.,2.,1.,2.,1.,2.,
1.,1.,2.,2.,1.,1.,2.,2.,
1.,2.,2.,1.,1.,2.,2.,1.,
1.,1.,1.,1.,2.,2.,2.,2.,
1.,2.,1.,2.,2.,1.,2.,1.,
1.,1.,2.,2.,2.,2.,1.,1.,
1.,2.,2.,1.,2.,1.,1.,2. ),nrow=8)
d<-read.csv("hell.csv", sep=';')
m<-as.matrix(d)
print( summary( m ) )
e<-rep( 0,8). #LWE error key
# 'normalize' matrix (in range p)
for (i in seq(8)) {
m[,i] = ( trunc(((p) * ( m[,i])/(1+max(m[,i])))) ) %% p
}
#matplot(m, type = c("l"),pch=1,cex=0.1)
# decrypt using inverse modular matrix
n = matrix( rep(0,8), ncol=8)
for (j in seq(nrow(m))) {
n <- rbind(n, dot( hinv , (m[j,] + p -e)%%p ) %% p )
}
summary(n)
plot( as.raster((n[50:150,]/3)))
Helloween radio using Adam Pluto SDR
The first script (appendix 1) modulates Helloween via a radio ‘SDR’ device . It outputs an IQ file with raw samples in stereo (2x 16 bits integer) that can be send to an SDR transmitter. In the code below, the IQ file (hell.iq) is send to a Pluto Adam device via libiio.
iio_attr -a -c ad9361-phy TX_LO frequency 438200000
iio_attr -a -c ad9361-phy RX_LO frequency 438200000
iio_attr -a -c -o ad9361-phy voltage0 sampling_frequency 30720000
iio_attr -a -c -o ad9361-phy voltage0 rf_bandwidth 92000000
iio_attr -a -c -o ad9361-phy voltage0 gain_control_mode 'manual'
iio_attr -a -c -o ad9361-phy voltage0 hardwaregain '0'
cat hell.iq| iio_writedev -u ip:192.168.2.1 -b 1024 -s 6553600 cf-ad9361-dds-core-lpc

Helloween receiver (rtlsdr + sdr#) and decoder
It wasn’t possible to receive a signal while sending it at the same time, so i set up a second SDR device and recorded it via SDR sharp. A script in R to visualize a raster and an example is below.
The decoder for the recorded IQ file is in appendix 2 below.
#raster-visual.R
d<-read.csv("rtlhell.csv",header=F,sep=" ")
ddd<-dd/70000
ddd[ddd>1]=1
dm<-as.matrix(ddd)
plot( as.raster(dm))

APPENDIX 1: the Helloween encoder
#!/usr/bin/env python
from __future__ import print_function
# thanx to James Gibbard for iqtool :: iqgen.py
msg="""
* * **** * * ** * * **** **** * *
* * * * * * * * * * * ** *
**** *** * * * * * ** * *** ** * * *
* * * * * * * * ** * * * * * *
* * **** **** **** ** * * **** **** * **
* """.split("\n")[::-1]
import argparse
from sys import byteorder
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import hadamard
import sys
def generateTone(fs, toneFreq, numSamples, amplitude,col):
step = (float(toneFreq) / float(fs)) * 2.0 * np.pi
phaseArray = np.array(range(0,numSamples)) * step
#Euler's Formula: e^(j*theta) = cos(theta) + j * sin(theta)
amplitude = amplitude / float(len(msg))
wave = np.zeros(len(phaseArray))
for fci in range(len(msg)):
wave = wave + float(col[ fci ])*np.exp( float(fci)*1.0j * phaseArray) * amplitude
return wave
def complexToSingleArray(array):
realArray = np.real(array)
imagArray = np.imag(array)
output = np.zeros(realArray.size + imagArray.size)
output[1::2] = realArray
output[0::2] = imagArray
return output
# arguments
p = 3 # prime
h = ((1+hadamard(8))/2) % p
e = np.array( [0,0,0,0, 0,0,0,0] )
mode = ""
try:
mode = sys.argv[1]
e = np.array( [float(ei) for ei in sys.argv[2].split(",") ] )
except IndexError:
pass
print("e:%s mode:%s" % (e , mode), file=sys.stderr)
amplitude = ((2.0**15) - 1) # type is int16
with open("hell.iq", 'wb') as f:
for idx in range(100):
col = np.array( [ +1.0 if msg[mi][(idx)%len(msg[mi])] == '*' else 0.0 for mi in range(len(msg)) ] )
if "g" in mode:
col = h.dot( col.T ) # do ghost imaging
if "m" in mode:
col = (col + e ) % p
print (col)
output = generateTone(1e6,1000,655360, amplitude, col )
output = complexToSingleArray(output).astype(np.int16)
output.tofile(f)
f.close()
APPENDIX 2: The decoder
#!/usr/bin/python wav file
import numpy as np
import scipy.io.wavfile
import math
samplerate, data = scipy.io.wavfile.read('SDRSharp_20200821_123117Z_438255000Hz_IQ.wav')
print "samplerate", samplerate
left = channel1=data[:,0].astype(float)
nfft = 4096*4
step = (float(100) / float(samplerate)) * 2.0 * np.pi
phaseArray = np.array(range(0,nfft)) * step
for i in range(0,data.shape[0], nfft):
print i,
for b in range(1,2000):
print abs( np.sum( left[ i:(i+nfft)] * np.sin( float(b)*phaseArray ) ) ),
Internet-of-People (IoP)
[2] http://qsl.net/on4cko/me.html