Change of potentiometer linearity

February 2019

• Problem definition
• Analysis
• Result
• Scale example
• Summary

Problem definition

Voltage regulation using linear potentiometer is not in all occasions optimal. For example in case of laboratory power supply maximum output current potentiometer area of small current values is really a small part of the scale. Problem can be solved using potentiometer with nonlinear characteristic (logarithmic). Potentiometers of that kind can be found on the marked, but also with linear potentiometer there are a good possibilities.

Analysis

There is a possibility to modify linear potentiometer to that one similar to logarithmic or exponential using additional resistor. Depending on the location where it is added the result is similar to logarithmic or exponential. That means scale is expanded in the lower or the upper part.

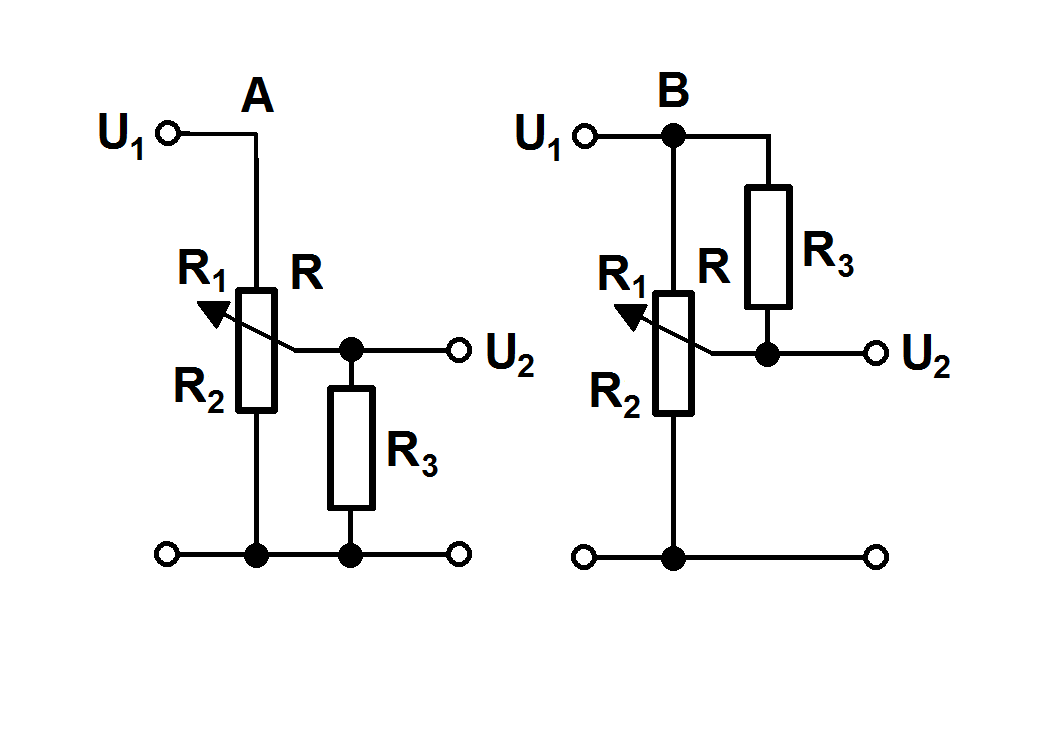
Additional resistor can be added or between middle and lower end (case A) or middle and upper end of potentiometer (case B). Depending on value of added resistor comparing to potentiometer resistance it results in more or less significant change. In general the smaller the resistor the bigger the change.

For the purpose of problem analysis there will be introduced so called "normalisation":

• angle of potentiometer axis will be expressed in relative measure α = angle/angle_max, where angle_max is potentiometer maximum angle. α can achieve values 0..1.
• division ratio of potentiometer q = U₂/U₁ can also achieve only values between 0..1.
• potentiometer resistance R can be at any moment described as sum of resistance of lower and upper part R = R₁ + R₂, consequently it can be written:
  R₁ = R x α
  R₂ = R x (1 - α)
  
• additional resistor R₃ can be described as multiplication of R:
  R₃ = k x R

Using those substitutions one can derive equations shown below. They are showing both dependency of angle on division ratio as well as opposite - division ratio as dependency on angle.

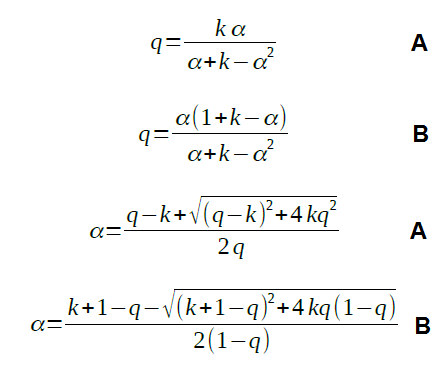
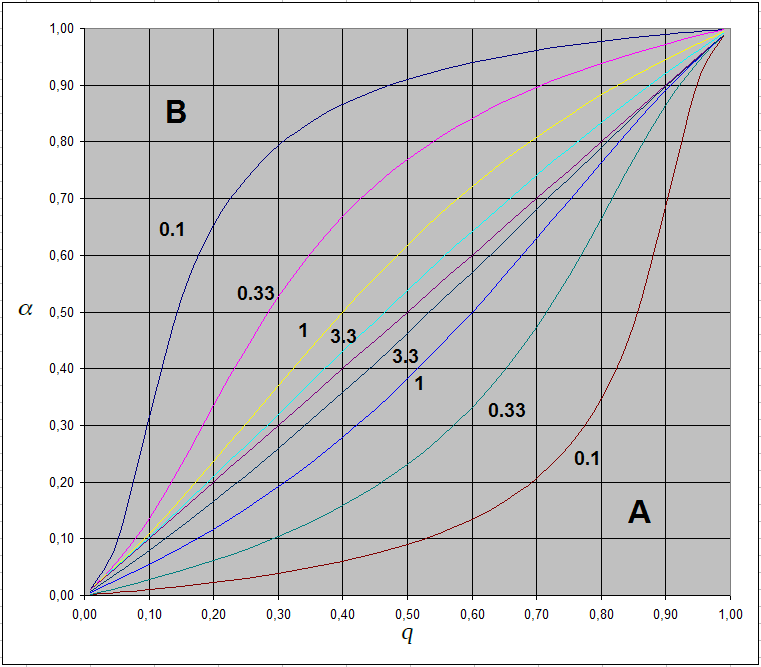
The equations may look difficult, but they can be easily handled using spreadsheet program (for example MS Excel, LibreOffice Calc or so) and in result definition file for scaler program can be prepared.

Graphs

Using spreadsheet processor series of calculations were performed for case A and B and k equal 0.1, 0.33, 1 and 3.3 (R₃ as multiplication of R).

As it can be seen R₃ having tenth value of R has very strong influence on potentiometer angle/division ratio. Even 1/3 of R is still very visible. Scale example shown below was calculated for the case A and R₃ = R (k = 1).

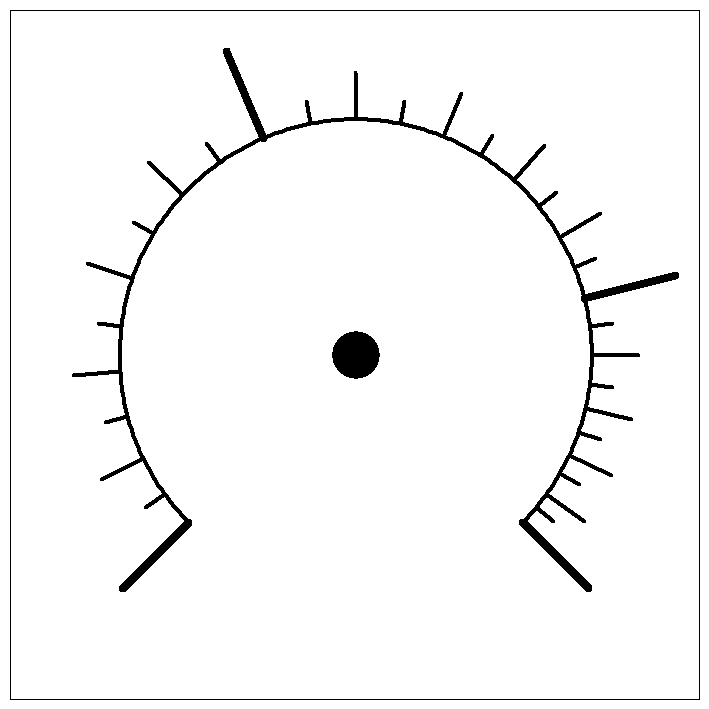
Scale example

Summary

Using procedure described in this contribution it is possible to modify linear potentiometer characteristic to be similar to logarithmic or exponential. Equations shown above allow calculation of potentiometer scale parameters depending on requirements.

A few details at the end - definition file for example scale was prepared as follows:

1. maximum potentiometer angle was taken 270° (in real deployment it would be suggested to measure real value using ohmmeter and goniometer, which would result also in real values of left and right scale angle, which may not be 225° and -45° then)
2. in spreadsheet it was made column of scale values in sense of division ratio (q) 0,033, 0,066, 0,099, ... 0,967 (values 0 and 1 are not used, they generate error, which is mathematically correct). Scale segments are defined as 15 segment scale with small half sized markers (30 segments all together). Cell value is defined as "=(previous cell)+1/30"
3. next column is filled using equation - case A and equation for q and the whole column is processed
4. next column is filled with recalculation "=(left cell value)*270-45"
5. the whole column is completed and format is set not to show decimal places at all
6. using clipboard the whole column is transferred to text editor and "m", "s" a "n" is completed as required. Left and right angle must be in the program defined according reality.