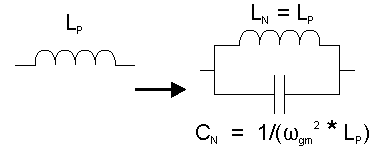
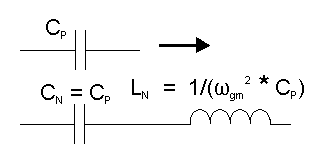A translation from a low pass prototype to a band stop filter requires three steps. The first of which is to do a resistance translation (q.v.) and second to do a high pass frequency translation using this conversion factor.

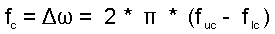
Be warned that the corner frequencies mentioned are not down at the bottom of the band stop curve. The corner frequencies are at the 3 dB down points on the curve. Go to Help-Data Entry-Band Stop in the main menu.

Having done those two translations, find the geometric mean of the two frequencies f _uc and f _lc by using

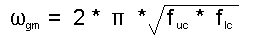
The geometric mean and the arithmetic mean are only a few percentage points different when pass bandwidths are small, but can become large when bandwidths increase.

To complete the bandstop transformation, each capacitor becomes a series resonant circuit which is resonant at the geometric mean frequency. Each inductor becomes a parallel resonant circuit which is resonant at the geometric mean frequency. To translate from the previously prepared capacitance values, perform this mathematical manipulation:

To translate from the previously prepared inductance values to the parallel resonant circuit, perform this mathematical manipulation:

With band stop filters, the interest is in attenuating a range of frequencies from a to b at the 3 dB level and a second range of frequencies from c to d at a greater attenuation. Conceptually, first consider the range c to d first as in "I really need to lower the television channel 2 (54 MHz to 60 MHz) interference by about 20 dB." Consider a second band where the attenuation is at the 3 dB level. Perhaps the band could be from 50 MHz to 64 MHz where a third order filter would do nicely.

Band stop filters have a deep "V" shape and the deepest point of the V is not located at the arithmetic mean of the band specified.

If a single frequency is the problem, the deepest part of the V must be at that frequency. The Butterworth Calculator gives the option of selecting "Notch" which will place the deepest part of the V and the greatest attenuation on that frequency. Select some accompanying bandwidths for purposes of selecting the order. Higher orders will give deeper notches. Without doing a simulation, the attenuation at the bottom of the notch remains unknown. A recent simulation showed an attenuation in excess of 550 dB when using a thirteenth order filter, which gives no realistic information.