|
Inverse Iteration with Shifts
This program uses the inverse iteration method to solve the eigenvalue problem:
Ax =( lambda)Bx
This method converges to the lowest eigenpair (A1, E1), provided the starting iteration vector (X0) is not
orthogonal to E1.
To avoid the limitations of convergence only to the lowest eigenpair, the program allows the user to
"shift" to any eigenpair, as shown in the figure below.
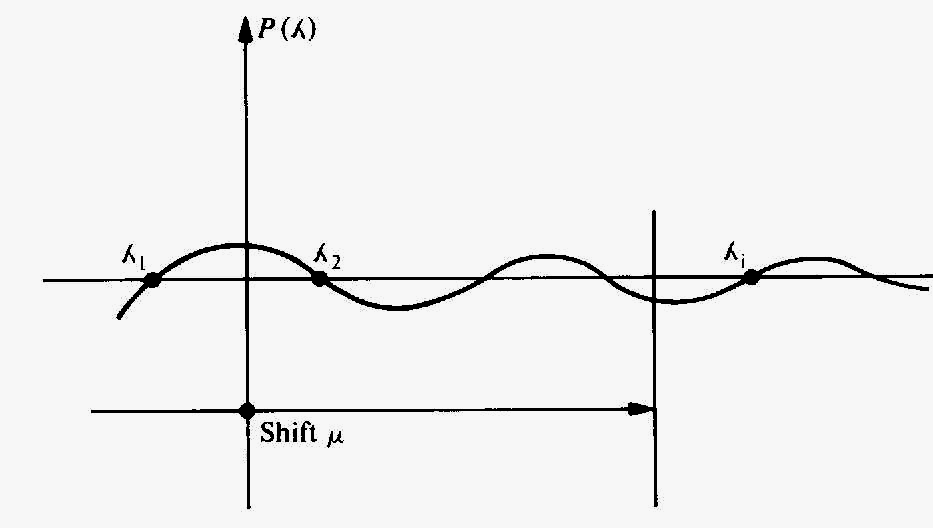
The introduced shift 'mu' will determine convergence to A (which is the closest value to mu). Furthermore, the introduction of the shift allows the following:
* An improvement in the order of convergence,
* Matrix A does not have to be either positive definite or non-singular,
Program Notes:
The data that this program requires is as follows:
*The dimension N,
*The matrix A (Note: since the matrix is assumed to be symmetrical, you need only enter the upper triangle by columns,)
*The matrix B, Two options are available:
Type I: B is a diagonal matrix and the user need only enter the diagonal elements,
Type 2: B is a full symmetrical matrix, Again, the user need only enter the upper triangle,
*Error tolerance E, The solution will only be evaluated for an eigenvalue within the specified tolerance,
The following parameters are under your control during program execution:
*Maximum number of iterations, NMAX, to be performed in the inverse iteration procedure
*Shift
The arrays in this program A,A1, B, U, and Z have been dimensioned for a matrix which is 15 x 15. For a matrix larger than 15 x 15, change the dimension statement in line 1 as follows:
DIM A(N(N+1)/2), B(N(N+1)/2), A1(N(N+1)/2), U(N). Z(N)
where N is the maximum size dimension.
The starting iteration vector has been chosen so that its components are the diagonal elements of matrix A divided by the corresponding diagonal elements of matrix B. To redefine this, delete these lines and substitute the desired expression.
REM ==INITIAL EIGENVECTOR==
II =0
FOR I = 1 TO N
II = II + I
B1 = B(I)
IF I9 = 1 THEN 1320
B1 = B(II)
U(I) = A(II) / B1
NEXT I
Example (test case - see below):
Consider the following:

Downloads:
Baisic program - liberty basic-lbits.bas
Basic program - qbeigit.bas - Qbasic program
Test case:
INVERSE ITERATION WITH SHIFTS
TYPE (1) DIAGONAL MATRIX
TYPE (2) FULL SYMMETRICAL MATRIX
ENTER TYPE OF PROBLEM
TYPE = 1
DIMENSION MATRIX A
N = ?3
>ENTER MATRIX A UPPER TRIANGLE
UPPER PART COLUMN 1
A( 1,1)= ?0
UPPER PART COLUMN 2
A( 1,2)= ?1
A( 2,2)= ?0
UPPER PART COLUMN 3
A( 1,3)= ?1
A( 2,3)= ?1
A( 3,3)= ?0
INPUT VECTOR B
B(1) =?1
B(2) =?1
B(3) =?1
>ENTER TOLERANCE
ORDER OF TOLERANCE X (AS IN 1e-X)8
>MAXIMUM # OF ITERATIONS (PRESS ENTER FOR 50)
NMAX =
>INPUT DESIRED SHIFT
SHIFT = 0
RUNNING
**ERROR** UNSUCCESSFUL FACTORIZATION
CHOOSE NEW SHIFT
>INPUT DESIRED SHIFT
SHIFT = 4
RUNNING
NUMBER OF EIGENVALUES
SMALLER THAN SHIFT = 3
DETERMINANT = -50
WANT SHIFT CHANGED (Y/N)?N
RUNNING
>SOLUTION
********
EIGENVALUE
EIG = 2.0
EIGENVECTOR
U(1)= 0.57736279
U(2)= 0.57735255
U(3)= 0.57733548
NUM. ITERATIONS
N = 9
WANT ANOTHER EIGENSOLUTION (Y/N) ?Y
>MAXIMUM # OF ITERATIONS (PRESS ENTER FOR 50)
NMAX =
>INPUT DESIRED SHIFT
SHIFT = -5
RUNNING
NUMBER OF EIGENVALUES
SMALLER THAN SHIFT = 0
DETERMINANT = 112.0
WANT SHIFT CHANGED (Y/N)?N
RUNNING
>SOLUTION
********
EIGENVALUE
EIG = -0.99999999
EIGENVECTOR
U(1)= 0.74929851
U(2)= -0.93628721e-1
U(3)= -0.65558021
NUM. ITERATIONS
N = 24
WANT ANOTHER EIGENSOLUTION (Y/N) ?Y
>MAXIMUM # OF ITERATIONS (PRESS ENTER FOR 50)
NMAX =
>INPUT DESIRED SHIFT
SHIFT = -1.0001
RUNNING
NUMBER OF EIGENVALUES
SMALLER THAN SHIFT = 0
DETERMINANT = 0.30001e-7
WANT SHIFT CHANGED (Y/N)?N
RUNNING
>SOLUTION
********
EIGENVALUE
EIG = -1
EIGENVECTOR
U(1)= 0.81649658
U(2)= -0.40821767
U(3)= -0.40827891
NUM. ITERATIONS
N = 3
WANT ANOTHER EIGENSOLUTION (Y/N) ?Y
>MAXIMUM # OF ITERATIONS (PRESS ENTER FOR 50)
NMAX =
>INPUT DESIRED SHIFT
SHIFT = -1
RUNNING
**ERROR** UNSUCCESSFUL FACTORIZATION
CHOOSE NEW SHIFT
>INPUT DESIRED SHIFT
SHIFT = -.999999
RUNNING
NUMBER OF EIGENVALUES
SMALLER THAN SHIFT = 2
DETERMINANT = 0.2999999e-11
WANT SHIFT CHANGED (Y/N)?N
RUNNING
>SOLUTION
********
EIGENVALUE
EIG = -1
EIGENVECTOR
U(1)= -0.81649658
U(2)= 0.4082486
U(3)= 0.40824798
NUM. ITERATIONS
N = 3
WANT ANOTHER EIGENSOLUTION (Y/N) ?N
|
