Hi, I am Tony
I0JX
Selecting capacitors in RF power applications
at HF
FOREWORD
I decided to write this page after realizing that, in the literature regarding capacitors for RF applications, topics are often discussed in non-homogeneous manner, and it is therefore difficult to get a clear understanding of the issues. Also, product catalogs of different manufacturers show data that are sometimes hard to compare.
After consulting and correlating material from several sources, I did my best to derive (what I hope is) a consistent vision of the matter, and I then tried to present it in a manner as consequential as possible.
The discussion is here limited to applications at HF (1.8 ... 30 MHz), as beyond that range capacitor modelization becomes much more complex and requires mathematics that out of the scopes of this web page.
Someone may find my text a bit heavy to read: was it Einstein who used to say "one shall explain things in the simplest possible way, but not simpler than that"?
THE ISSUE
Selecting a capacitor is most often not a critical thing, just select the proper capacitor type with a DC voltage rating that fits your needs. But if your application involves a circuit handling a substantial amount of RF power, you must also consider the RF voltage that develops across the capacitor and the RF current flowing through it, them both causing the capacitor temperature to rise, with potentially dangerous effects. A temperature change will in turn cause a variation in capacitance, and this may result in e.g. a possible de-tuning of the resonating circuit in which the capacitor operates. Furtheremore capacitor temperature shall never exceed some 95 degrees, as beyond that value the crystalline structure of the ceramic dielectrics may permanently change (this occurs at the Curie temperature, which is in the 120°C range, and varies with the particular material).
PHYSICAL EFFECTS AND RESULTING ELECTRICAL LIMITS
Three are the main physical effects that occur within a capacitor and that have to be duly taken into account when selecting the component, namely:
discharge or breakdown due to excessive voltage across the capacitor;
heating due to ohmic effects;
heating due to loss within the dielectric .
As to item (i.), it is well known that, beyond a certain voltage, the capacitor will fail due to electrical discharge or breakdown. There usually are both a "normal voltage" (Vn) and a "peak voltage" (Vp) specification, the former being the maximum voltage at which the capacitor will not be subject to a premature failure, the latter being the maximum voltage that the capacitor can safely withstand for short periods (e.g. 1 minute). Vp is anyway much lower than the voltage at which the capacitor will immediately break. Rule of thumb: the higher the voltage applied to the capacitor, the shorter its life. In RF power circuits, the voltage across the capacitor has often both a DC (vdc) and an RF component (vrms), that add up to each other; to a first approximation what counts with regard to discharge is just the sum of vdc and vrfp (with vrfp = 1.41 vrms). In conclusion the electrical discharge phenomenon sets a limit (Vn) to the total voltage (vdc + vrfp) that can be applied to the capacitor. In the HF range such limit can be considered to be independent of frequency.
Please note that, as a general rule, capital letters (e.g. Vn) are here used to indicate limits or specifications, while small letters (e.g. vrms) are used to indicate actual values.
As to item (ii.), power loss due to ohmic effects occurs in the metallic structure of the capacitor (e.g., electrodes, terminations) due to their non-zero resistance (ohmic loss also occurs in the dielectric due to its non-infinite resistance, but this usually causes a negligible power dissipation). This so-called metal loss depends on the specific conductive properties of all metallic materials used in the capacitor, and it is often not neglibile at all, with a consequent rise in temperature. This effect can be modelled as a resistance of value Rm in series with the capacitor, that causes a power loss equal to Rm (irms)2, where irms is the r.m.s. RF current flowing through the capacitor.The value of Rm increases with frequency mainly due to skin effect; however, if we limit ourselves to the HF range, the total change of metal loss across the full range will typically be less than 20%. In conclusion the metal loss phenomenon causes a power loss that heavily increases with RF current, and therefore sets a limit (In) to RF current (irms) that can flow through the capacitor. Such limit can be considered to be nearly independent of frequency.
As to item (iii.), power loss also occurs in the dielectric, resulting in capacitor temperature rise. Such loss is bound to the magnitude of the alternating electrical field existing in the dielectric, which in turns depends on applied RF voltage. Physically, the so-called dielectric loss can be associated to the stress that field causes on the dielectric structure. For a given vrms, dielectric loss increases with frequency; this fact can be visualized by considering that, at each RF cycle, some energy is dissipated within the dielectric, therefore increasing the number of cycles per second (having care to keep vrms constant), the dissipated power will also increase. A way of modelling dielectric loss is that of considering a resistance of value Rd in parallel with the capacitor, that causes a loss equal to vrms2 / Rd. It can be shown that Rd = Xc / Df, where Xc is the capacitor reactance, and Df is the so called dissipation factor of the material, often also termed tand, which is independent of frequency (at least within the HF range). The presence of the factor Xc justifies the fact that, as already said, keeping vrms constant the dielectric loss of a given capacitor increases with frequency (dielectric loss can however also be expressed as Xc Df irms2, a formula showing that, keeping instead irms constant, dielectric loss decreases with frequency). For specifications purposes, it is however more convenient to utilize an expression in which dielectric loss results to be independent of frequency; this is possible by expressing dielectric loss as a function of the reactive power (pr) applied to the capacitor (pr = vrms irms). It is easy to demonstrate that dielectric loss simply equals pr Df, this witnessing that, keeping pr constant, the dielectric loss of a given capacitor is independent of frequency. It should be noted that Df is usually measured at low frequencies (e.g. 1 MHz or lower), where metal loss is comparably much lower (and measurable dielectric loss effects can be obtained with a smaller irms). The pr of a capacitor shall not exceed a limit (Pm) that is usually determined as the reactive power causing temperature not to rise above 45°C. In conclusion the dielectric loss phenomenon causes a power loss that increases with both vrms and irms, and therefore sets a limit (Pm) to the reactive power (pr) that the capacitor can handle. Such limit can be considered to be independent of frequency. Note that the same pr value can be obtained with different pairs of vrms and irms, their ratio depending on Xc and hence on capacitance. This explains why capacitors of different values, but having the same reactive power specifications, may withstand different maximum vrms or irms values.
I do not want to further confuse your ideas, but in the literature I often found references that attribute both the heating effects (items ii. and iii. above) to a single parameter called ESR (Effective Series Resistance), where ESR = Rm + (Xc)2 / Rd. By this approach dielectric loss is treated just the same way as metal loss, i.e. as a series resistor of value (Xc)2 / Rd. The total power dissipated in the capacitor then simply becomes ESR(irms)2. Unfortunately ESR varies significantly with frequency, so it is not a simple parameter to specify. Furthermore, knowing ESR is not sufficient to calculate the maximum permissible irms for a capacitor, it also being necessary to know its maximum allowable power dissipation. In conclusion, for our purposes we prefer to use the previous definitions, despite ESR certainly is a widely used parameter.
APPRECIATING CAPACITORS SPECIFICATIONS
From what said in the previous section, it appears that the main electrical parameters that have to be specified with regard to RF power capacitors are three, which are all independent of frequency (or nearly so, at least in the HF range):
Vn: the maximum value of the DC + peak RF voltage (vdc + vrfp) that can be steadily applied to the capacitor without shortening its life;
In: the maximum value of the RF current (irms) that can steadily flow through the capacitor without overheating it;
Pm: the maximum value of the reactive power (pr) that the capacitor can handle without overheating.
Unfortunately, not all manufacturers' catalogs clearly indicate the three above specifications for each capacitor, so it is not always easy to decide whether a capacitor would be suitable for your application. At this regard please remember that:
both irms and pr contribute in heating the capacitor. So, if both parameters result to be high enough compared to their limits (In and Pm respectively), then some derating will be necessary;
for non-continuous operation (e.g. SSB or CW), the capacitor can operate at limits higher than In and Pm (what counts with regard to heat generation is the average dissipated power).
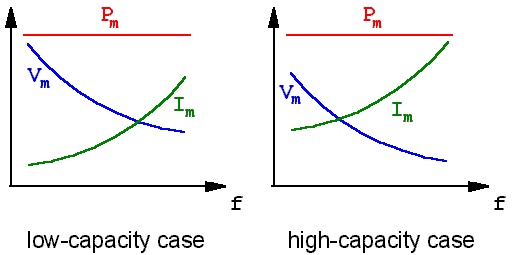
It should also be observed that setting a limit (Pm) to the reactive power implicitly means also setting a limit to the voltage (Vm) and to the current (Im) that create that reactive power (Pm = Vm Im). For a given Pm however, Vm and Im are not unequivocally determined, as they vary with frequency and capacitance (consider that Im = Vm / Xc). This behaviour is visualized in the following pictures, The graph on the left hand side shows how Vm and Im vary with frequency (f) for a given Pm. The graph on the right refers to a capacitor of higher value but with same Pm; it is evident that, at each frequency, the ratio between Vm and Im has decreased due to the lower capacitor Xc.

That said, it is important to remark that Vm derives from a physical phenomenon different from that causing Vn, therefore the Vm and Vn figures have no relationship with each other. The figure to be actually used for determining the maximum vrms that can be applied to a capacitor will then be the lower of two. Identical reasoning applies to Im and In. Picture below shows the corrisponding behaviours.
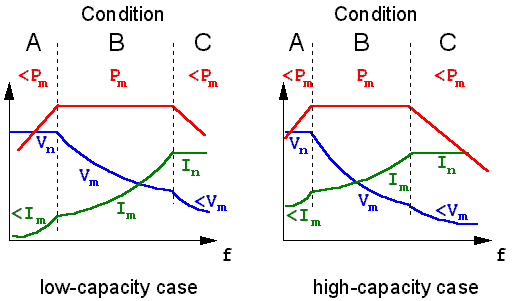
The graphs reflect the fact that, as already said, the actual limit for vrms will be the lower between Vm and Vn (same applies to Im and In). It is then possible to define three operational conditions (see graphs):
condition A: this is the discharge-limited condition, where Vn results to be more constraining than Vm. As vrms cannot anyway exceed Vn, the actual pr will be lower than the maximum permissible value (Pm). Also irms will be lower than that (Im) corresponding to Pm;
condition B: this is the dielectric-limited condition, where the actual limit is represented by Pm. Just multiply vrms by irms to verify that you are within Pm;
condition C: this is the ohmic-limited condition, where In results to be more constraining than Im. As irms cannot anyway exceed In, the actual pr will be lower than the maximum permissible value (Pm). Also vrms will be lower than that (Vm) corresponding to Pm.
For a given capacitor (i.e. for given Vn, In and Pm), the above defined operational conditions will only depend on frequency, and not at all on the actual vrms and irms values.
TYPES OF RF CAPACITORS
Let us now pass to consider products available on the market. Air-insulated capacitors would be ideal for RF applications, them not being subject to dielectric loss; unfortunately they are very bulky. Making the capacitor with a material having a dielectric constant (k) higher than that of air (k = 1) permits to reduce capacitor size; the formula is very simple: for a given physical capacitor geometry, capacitance is just proportional to k. The market of capacitors for RF applications is today dominated by ceramic capacitors that feature very high k values, up to 10,000 or more.
Selecting a dielectric with a high k yields however some drawbacks, the most important ones being:
the Temperature Coefficient of Capacitance (TCC), which is the maximum change in capacitance over a specified temperature range, increases and tends to show a non-linear behaviour;
the dissipation factor also increases;
tight tolerances are not easy to achieve;
actual capacitance becomes sensitive to the applied vdc (capacitance may drop down to 50% of its nominal value when vdc = Vn);
higher aging rate, a phenomenon due to the relaxation of the microcristalline structure that causes capacitance loss with time, due to a reduction of k. A high-k capacitor could lose up to 25% of its capacitance 4,000 hours after fabrication, but after that capacitance loss becomes much slower.
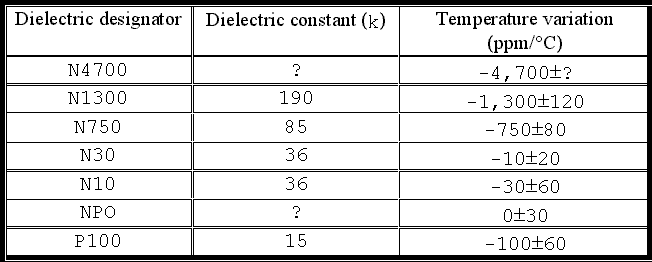
Type-1 dielectric is material with low k (say less than 200). The TCC for type-1 dielectric, expressed in parts per million per degrees centigrade, is quite moderate. The temperature characteristic of a type-1 dielectric is directly related to its k, as shown in the following table.
Capacitors built with type-1 dielectric are called RF power capacitors; they usually feature a Vn greater than 1kV, an In greater than 1A, a Pm greater than 1kVAr, an almost linear temperature coefficient of less than 1,300ppm/°C and a dissipation factor of less than 0.001. Picture below shows typical RF power capacitors. They are used in applications where temperature stability is important (e.g. resonating circuits) and high Q is required.

Low-capacity (e.g. < 1,000pF) disc-type capacitors with wire leads are most often also built with type-1 ceramics and then have characteristics similar to those of the RF power capacitors.
Type-2 dielectric is material with high k (up to 5,000 or even more). In this case TCC is much higher, varies with temperature, and is usually expressed in percentage of capacity change. A three-symbol designator, e.g., Z5U, X5V, is used to characterize the temperature behaviour of the capacitor (you may have read such strange markings, most often on wire-lead disc-type capacitors). Their significance is shown in the following table.
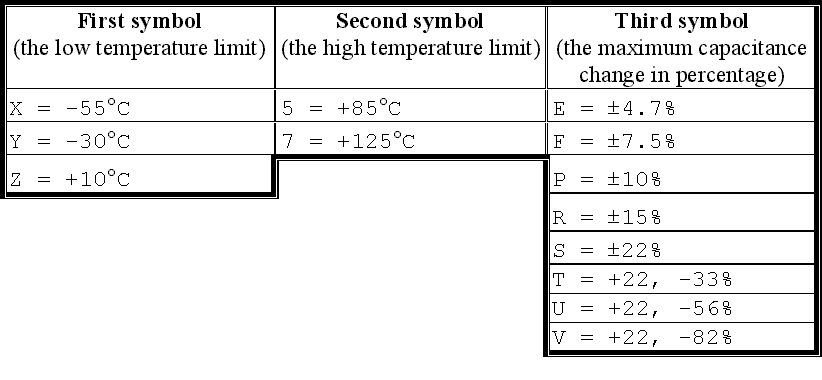
For instance, the Z5U designator indicates a capacitance variation of +22% / -56% across the temperature range +10°C / +85°C.
Also for type-2 dielectric the temperature characteristic is bound to k, as presented in table below.
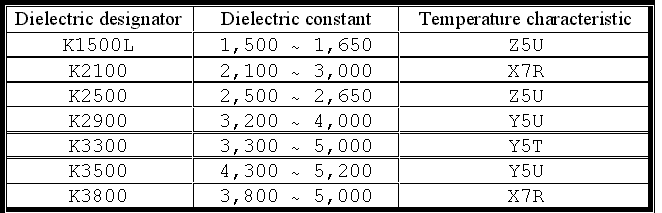
The nominal capacity indicated by the manufacturer is referred to a temperature of 25°C. As already mentioned, for type-2 dielectric capacity change vs. temperature is highly variable and non linear.
Capacitors built with type-2 dielectric are usually called high-voltage capacitors, that should not be confused with the RF power capacitors discussed before, though their appearance may sometimes be similar and despite they are both commonly referred to as doorknob-type capacitors, as they appear like small barrels with axial wire leads or screw terminals. The design of high-voltage capacitors is optimized for operation at very high Vn, even up to 250kV. They can also withstand a fairly high irms, while their Pm is usually limited. They typically feature very high and non-linear temperature coefficients (up to 70,000 ppm/°C), a higher dissipation factor (up to 0.015) and a remarkable capacitance variation with DC voltage. Picture below shows typical high-voltage capacitors.

Generally speaking, high-voltage capacitors look taller and sometimes even fatter than RF power capacitors, but it is not always easy to distinguish. A capacitor higher than 5,000 pF having a Vn of 10kV or more is most likely a high-voltage capacitor.
It should be noted that wire-lead disc-type capacitors with a voltage specification higher than some 500V and with capacity higher than 1,000pF are commonly built with type-2 dielectric. Therefore they have characteristics similar to the high-voltage capacitors.
In summary, high-voltage capacitors can also be used in RF circuits, but their usage shall be limited to applications not requiring a high stability of capacitance, and very high pr; conversely they can sustain significant irms values.
That said, let us consider a very well-known product, i.e. the Centralab doorknob ceramic capacitors (now manufactured by ITT-Jennings). They come in several sizes, the most common one being that of models 850 and 858. Model 850 (now renamed HT50), shown below, is an RF power capacitor with capacity varying from 10pF to 500pF, temperature coefficient varying from NPO to N4700, and a Vn of 5kV or 7.5kV. For what concerns In, it seems reasonable to assume that In coincides with the specification they give for maximum current at 30 MHz, which ranges from 7A to 10A depending on capacity. For what concerns the maximum reactive power (Pm), they do not use this term, but they indicate maximum current (Im) at selected frequencies; e.g., for the 100 pF unit, 3.6A @ 1 MHz and 6.8A @ 10 MHz.

Model 858 (now renamed HT58) looks very similar to model 850, the main apparent difference being the fact that the ceramic wall is just a bit thicker, but it has higher capacity, i.e. 1,000pF (a 500pF unit was also available, but now presumably no longer produced). The Vn rating is the same of the 850 model (i.e. either 5kV or 7.5kV), In is 5.6A, and Im is 1.6A @ 1MHz or 3.8A @ 10MHz. Model 858 utilizes type-2 ceramics (type X5V) and should therefore be regarded as a high-voltage capacitor.
It should be noted that other Centralab doorknob capacitors (i.e. the smaller 853-, 854- and 855-types, the larger 857-type and the king-sized 859-type are all RF power capacitors). Therefore model 858, which is probably the most used type, constitutes an exception to the rule
FROM THEORY TO PRACTICE
Let us now consider a typical RF power amplifier (a grid-driven neutralized tetrode) and discuss the type of capacitors that are needed for the functions. Picture below shows a simplified schematic diagram of the amplifier, in which all components irrelevant for the issues to be discussed have purposely been omitted.
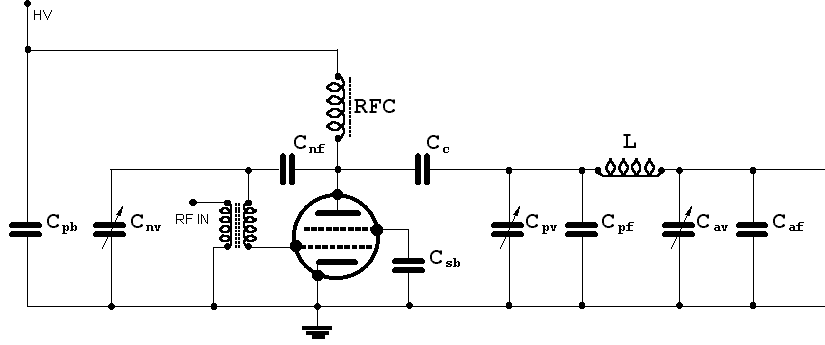
Only fixed capacitors are of our interest:
Cpb is the plate bypass capacitor;
Cnf is the fixed neutralization capacitor;
Csb is the screen bypass capacitor;
Cc is the coupling capacitor;
Cpf is the plate fixed padding capacitor (if needed), in parallel to the plate variable capacitor Cpv;
Caf is the antenna fixed padding capacitor (if needed), in parallel to the antenna variable capacitor Cav.
It would obviously be possible to utilize RF power capacitors everywhere, but such a choice could be an overkill in cases where a high voltage capacitor can do the job equally well. As a matter of fact RF power capacitors with the required capacitance and Vn may be unavailable, too expensive or too bulky. In conclusion, it is worthwhile to individually address the various capacitors, with the aim to understand their respective requirements.
The plate bypass capacitor Cpb shall be selected with a Vn safely dimensioned with regard to vdc only, as vrms will anyway be very low, the purpose of Cpb being just that of quenching RF on the HV line. This is the reason why Cpb shall feature a low Xc across the whole frequency range, and shall then have quite a high value (at least 1,000 pF, or better more than 10,000 pF for 80- or 160-meter operation). High-voltage capacitors can well be used; on the one hand they offer such high capacitance values in conjunction with the required Vn, on the other hand their limited tolerance and high TCC do not represent an issue for bypassing purposes. With reference to the previously shown graphs, high capacitance will tend to shift the inter-condition boundaries much to the left, but their actual position will depend on the capacitor In, Vn and Pm specifications. For instance, with a 15,000 pF Morgan model-858 capacitor (Vn = 3.5kV, In = 15A, Pm = 1.5kVAr) having an Xc of some -6 ohm at 1.8 MHz, the 15A limit corresponds to an hypothetical pr of about 1.3kVAr, which is lower than Pm. This means that, for said parameters and across the whole ham radio frequency range, Cpb would stay in condition C (ohmic-limited condition). This fact is however not too meaningful as, in practice, irms should be not too high, unless the RFC inductance is undersized. Withn a proper RFC design, much smaller capacitors than the Morgan model-858 taken above as example can typically be used, even wire-lead disc-type capacitors could do, but verify first that RFC inductance is properly dimensioned at the lowest frequency range, otherwise you may have unpleasant surprises.
The fixed neutralization capacitor Cnf shall have a very high Vn, it being subjected to about the sum of vdc and vprf. To stay on the safe side, select a capacitor with Vn higher than twice the plate voltage. Only RF power capacitors can be used for this application, a low TCC being required for stable operation of the neutralization bridge. The Cnf capacitance is usually very low (just a few pF), a fact causing the shift of the inter-condition boundaries much to the right. For instance, assuming a vdc of 2.3kV and a vrms of 1.7kV, with a 2 pF Morgan model-10 capacitor (Vn = 4kV, In = 2A, Pm = 4kVAr) having an Xc of some -2,600 ohm at 30 MHz, the pr corresponding to the vrms of 1.7kV would be some 1.1KVAr, that is lower than Pm. This means that, with said parameters and across the whole ham radio frequency range, Cpb would stay in condition A (discharge-limited condition). The above mentioned type-10 capacitor would however not be the best possible choice for our case, as its Vn of 4kV offers no margin with respect to vdc + vrms, while its In and Pm would be more than adequate.
The screen bypass capacitor Csb does not require a very high Vn because of the rather low screen DC voltage (usually 300 to 500V, or slightly more); furthemore vrms will also be low because the purpose of Csb is just that of quenching RF on the screen. It should be noted that Csb shall feature a very low Xc across the whole frequency range, much lower than that of Cpb, a very effective grounding effect being needed for the screen. Therefore Csb shall have a very high value (e.g. in the range of several tents on nF for 80- or 160-meter operation). Only high-voltage capacitors can practically offer such high capacitance values; on the other hand tolerance and TCC are not important for bypassing purposes. With such high capacity values, it is very likely that Csb will stay in condition C (ohmic-limited condition) over the whole ham-radio frequency range, though this will also depend on the particular capacitor characteristics. Differently from Cpb, Csb could be subjected to a rather high irms, due to the plate-to-screen capacity which, at 30 MHz, could cause an irms of up to 5A, or even more, to flow through Csb. Among the possible solutions, a widely used approach for Csb is that of using several (e.g. 10 or more) high voltage capacitors in parallel, with a suitable Vn and each sharing a fraction of the total current. This also yields the advantage of a low-inductance path to ground. For instance, using sixteen 1000pF capacitors with Vn = 1kV and In = 0.5A could be adequate even for 160-meter operation, and with such arrangement it could even be possible to use wire-lead disc-type capacitors, though not the small-size types.
The coupling capacitor Cc can be selected with a Vn safely dimensioned with regard to vdc only, it being possible to assume that vrms will not be very high over the whole frequency range. For instance, even an undersized Cc of 500 pF would develop, for a typical 2,500W-class amplifier, a vrms of only 250V or so at 1.8 MHz, a value that is small compared to the plate voltage that could typically be some 3kV. It is not uncommon to see designs in which capacitance is too low for Cc to act as a real RF short circuit over the whole frequency range; on the other hand this is not a problem because, if Cc has a non-negligible Xc, this can be compensated for by a different adjustment of the pi-network elements. It should however be noted that the value of Xc can make a difference in selecting the type of Cc to be used. To make the distinction more clear, let us consider to an extreme case, i.e. that of a high-power amplifier in which the irms flowing through Cc is 7A (such a high value could correspond to either an extremely high power amplifier, or an amplifier with a low plate impedance, e.g. seveal low-voltage tubes in parallel). Two capacitance values are considered for Cc:
Cc = 470pF, to which an Xc of some -190 ohm corresponds at 1.8 MHz. The resulting pr is about 9.2kVA, a value that a high-voltage capacitor would hardly tolerate. An RF power capacitor, such as the Morgan model-832 (Vn = 5kV, Vn = 11A, Pm = 20kVAr) would instead be adequate. It is easy to determine that Cc would stay in condition B (dielectric-limited condition).
Cc = 15,000pF, to which an Xc of some -6 ohm corresponds at 1.8 MHz. The resulting pr is about 290VA, a value that a high-voltage capacitor, such as the Morgan model-858 (Vn = 3.5kV, In = 15A, Pm = 1.5kVAr) can instead tolerate. In this case Cc would stay in condition C (ohmic-limited condition).
In conclusion, suitably sized high-voltage capacitors can be used for Cc, provided that capacitance is high enough. The irms actually flowing through Cc will not be far from the DC plate current.
The plate fixed padding capacitor Cpf shall withstand a high vrms, i.e. the DC plate current times plate impedance. The actual irms will depend on the Cpv value, it increasing for low Cpv values, for a maximum equal to Q multiplied by the DC plate current. Cpf must have a low TCC as any capacity change would result in circuit de-tuning. For even better stability, it would also be appropriate to oversize it, so that temperature will not significantly rise. This means that Cpf shall be an RF power capacitor. Let us again refer to a 2,500W amplifier with Q=12 in which no Cpv is used. From pi-network formulas, it can be easily calculated that Cpf shall have Xc = -120 ohm, and will be subjected to vrms = 1.9kV and irms = 15.8A. The resulting pr is very high (30kVAr), and this is another reason to exclude the use of high-voltage capacitors. A high value of pr is a characteristic common to all capacitors forming part of resonating circuits. An adequate capacitor for a 14-MHz amplifier would be the Morgan model-849, with Cpf = 100pF, In = 18A, Pm = 55kVAr. In this case Cpf would stay in condition C (ohmic-limited condition).
The antenna fixed padding capacitor Caf shall withstand a fairly moderate vrms, i.e. the square root of 50 times the RF power. The actual irms will depend on the Cav value, it increasing for low Cav values, up to a maximum of about the same maximum current as Cpf. Considerations similar to those exposed for Cpf are also valid with regard to Caf, that must also be an RF power capacitor. Referring again to a 2,500W amplifier with Q=12 in which no Cav is used, Caf shall then have Xc = -25 ohm, and will be subjected to vrms = 350V and irms = 14.2A. The resulting pr of about 5kVAr is not as high as in the case of Cpf. An adequate capacitor for a 14-MHz amplifier would be the Morgan model-839, with Caf = 470pF, In = 18A, Pm = 55kVAr. In this case Caf would stay in condition C (ohmic-limited condition).
That's all for now folks...
Return to the I0JX home page