|
|
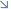 Eratostene Eratostene
La
misurazione del meridiano terrestre.
Quando
si parla della cultura dei greci, spesso ci si riferisce alla
filosofia ed alle grandi opere che essi ci hanno tramandato, ma
non bisogna mai dimenticare quei personaggi storici, che pur condividendo
i principi con i grandi pensatori del tempo, si sono distinti
in settori ben diversi. Uno
di questi, Eratostene, viene ricordato per la sua grande impresa
nel campo astronomico: la misurazione del meridiano terrestre.
Un'opera
che ai nostri giorni non susciterebbe tanto clamore, immersi come
siamo in un mondo tecnologico, ricco di strumenti che avrebbero
compiuto il lavoro per noi.
Ma
il merito dello studioso greco, vissuto nel terzo secolo avanti
cristo, sta proprio in questo. Ai suoi tempi infatti non esistevano
i computer, ne tanto meno le sonde spaziali, ed il suo lavoro
era frutto solo ed esclusivamente dell'ingegno o del Logos come
lo chiamavano loro. Per
ottenere questo, Eratostene tenne conto del fatto che la città
di Alessandria
si trova sullo stesso meridiano di Siene,
ma con latitudine differente, e che in quest'ultima città
il Sole al solstizio d'estate era pressochè a perpendicolo
e dunque proiettava un segmento d'ombra pari a zero.
Il
Sole allora, passando nel medesimo istante per il punto piu' alto
del cielo delle due località, proiettava l'ombra di due
aste uguali, situate una per città, in modo diverso a seconda
della latitudine.
Avendo
nota la distanza fra le due città, e considerando
che i raggi solari giungono paralleli sulla superficie terrestre,
Eratostene misurò la differenza dell'ombra ricavando l'angolo
di latitudine, da cui con una semplice proporzione ricavò
la lunghezza della circonferenza terrestre, con buona precisione,
visto che secondo i suoi calcoli ammontava a 39400 km, valore
poco lontano da quello vero di 40000.
Gli
angoli A1 ed A2 sono uguali perchè alterni interni di due
rette parallele, i raggi solari, tagliate da una retta, l'asta,
che essendo in verticale coincide con lo zenit di Alessandria
( a Siene l'asta coincide con i raggi perchè questi giungono
in verticale e perciò non danno ombra ).
|
|
Allo
stesso modo gli angoli A ed A1 sono uguali, perciò avremo
un triangolo di cui sono noti i cateti c e b dai quali, attraverso
la trigonometria, Eratostene calcolò l'angolo A.
Ma
quest'angolo è uguale all'angolo A2 perchè A1 =
A ed A1 = A2.
Siccome
gli angoli uguali sottendono archi di cerchi uguali, in questo
caso la parte di meridiano compresa tra le due città, con
una proporzione si ha la lunghezza del meridiano terrestre:
distanza
fra le città : angolo A2 = meridiano: 360 gradi
Avendo
la misura della circonferenza terrestre, e dunque il raggio terrestre,
Eratostene tentò di calcolare anche la distanza fra la
Terra e la Luna, avvalendosi fra l'altro dei precedenti tentativi
di un altro illustre studioso greco, Aristarco.
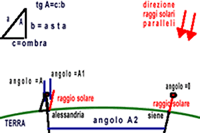
Partendo
infatti dai calcoli di Aristarco che aveva quantificato il disco
lunare in circa
2 gradi, e perciò contenuto
nella traiettoria dell'orbita lunare 180 volte, si accorse,
dal tempo che il disco lunare impiegava a transitare nel cono
d'ombra proiettato dalla Terra durante le eclissi, che questo
era pari a 3 volte
il cono d'ombra. Ma quest'ultimo poteva
essere considerato come un solido la cui base coincideva con la
sezione del globo terrestre ed il vertice posto all'infinito. Considerando
trascurabile la distanza fra la Terra e la Luna rispetto all'altezza
del cono, proiettata all'infinito, si otteneva che il diametro
lunare era un terzo di quello terrestre.
Avendo
quest'ultimo dato, calcolò la circonferenza ed il raggio
dell'orbita lunare.
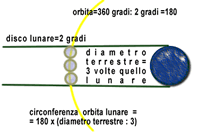
Facendo
un rapido calcolo otterremo un valore di 121000 km, valore ben
lontano da quello reale di 384400 km, anche se questo non sminuisce
affatto il merito di Eratostene, considerando la precarietà
della misurazione, compiuta senza l'ausilio di nessun strumento
tecnologico.
Documenti
|