If you add the number of homebrew passive diode ring mixers to the number of commercial SBL-1s and the like, diode ring mixers must be amateur radio's most popular mixer, outnumbering even the NE602. So, if you need to, read Chapter 5 of "Experimental Methods in RF Design" (ARRL 2003), then consider the following.

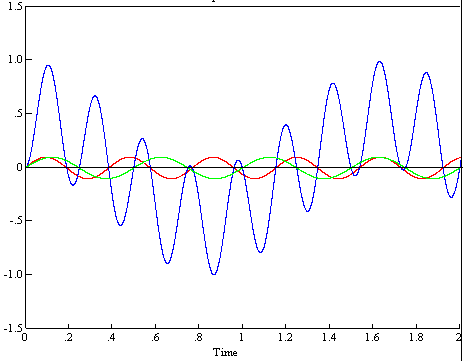
I have been asked why ring mixers are so inefficient. The first reply is that the mixer's output contains the sum and difference frequencies, so the loss of a simple (non-image recovery) mixer has to be greater than 3dB whatever else happens. But the detail is in the waveforms and the spectra, and for those with a steady nerve, phasors. Consider the waveforms in the following diagram, which illustrates the voltage waveforms associated with the perfect mixer.

This shows in red and green, small representations of 1Vptp LO and RF signals, and, in blue the full amplitude output from the perfect mixer. The 'perfect' mixer is a multiplier. It multiplies the instantaneous amplitude of the two input signals. That is why the symbol for the mixer is a ×, and it is also why we speak of mixing products and product detectors. Consider the following 3 conditions:

• When the LO voltage is instantaneously +1, then the IF output is instantaneously the same as the RF input.
• When the LO voltage is instantaneously zero, the IF output is also instantaneously zero. This can be seen in the figure: when either the LO or RF is instantaneously zero, the blue output is instantaneously zero.
• When the LO voltage is instantaneously -1, then the IF output is instantaneously the same as the RF input, but phase inverted.

If you think I have laboured the instantaneous voltage bit, it is for a very good reason. You may well use an oscilloscope to look at the inputs and outputs from an audio mixer, but you will use a spectrum analyser for an RF mixer. The oscilloscope picture and the spectrum analyser picture are related by the Fourier Transform. And if you put the blue curve in the diagram into the mathematical grinder, you come out with two frequencies that are the sum and difference frequencies of the input. So although the time waveforms are multiplied, the frequency spectra are added and subtracted.

You can intuitively see this by looking at the diagram above. The input signals are roughly the same frequency. So what does the blue trace look like? It's clearly composed of a low frequency component of about 1 cycle, with a superimposed high frequency wiggle that, having twice the zero crossings, must be twice the frequency. In other words, f_RF-f_LO and f_RF+f_LO.

A word on insertion loss. Imagine the RF input is DC coupled, and has a constant 1V dc applied to it. The output will be a sine wave at the LO frequency, and both f_RF-f_LO and f_RF+f_LO will occur at the same frequency. The maximum voltage that can appear is 1V at the peak of the waveform. The power will be √2 of the applied power. So the conversion loss in a ring mixer is 10log₁₀(√2). But the sum and difference frequencies are there nonetheless, so there is an additional loss of 10log(½). The total loss is a touch over 4.5dB, before considering the transformer loss and the non-ideal diode characteristics, an extra 1½ dB, totalling 6 dB.

The switching mixer has a much better strong signal handling performance than the normal analogue multiplier. So why aren't they all run like that? Consider the waveforms in the following diagram, which illustrates the voltage waveforms associated with the perfect switching mixer.

Although the same low frequency component is dimly visible, it is immediately apparent that a great many sharp edges have appeared. The harmonics of the LO that, in the analogue mixer, were confined to the LO circuit have now made it to the IF output.

An alternative classification for this mixer is the 2-phase commutating mixer, and it its logical function is summarised in the following diagram:

This brings us to the reason why mixers output the sum and difference frequencies, when we normally want only one of these. The answer lies deep in the mathematics, but this is what it all boils down to: a sinusoid is generated by a rotating phasor, and if you want to shift the frequency in one direction only, then you have to know which direction the phasor is rotating in the first place.

Imagine someone swinging a weight round on the end of a short piece of string overhead. If you are some distance away, you will be able to tell that the weight is rotating, because you will be able to see its sinusoidal motion. But if you can't see the string, you cannot tell which way round the weight is swinging: clockwise or anti-clockwise? If you want the frequency to increase, you ask the person with the weight to swing it round faster.

Intuitively, you know what faster means, but mathematically it means increasing the speed of rotation in an anti-clockwise direction. So if the weight was in fact rotating clockwise, faster means slower OK?

The way of sorting out this difficulty is by looking at the weight from two different positions at once. You could do this by setting up a mirror some distance away in which you could see the rotating weight. You could then tell whether the weight reached its maximum apparent distance from the centre earlier or later in the mirror image compared to what you observe directly. And that is why direct conversion receivers with image rejection have two signal channels.

But with only one phase representation, you can't tell which way the phasor is rotating, so what does the 2-phase commutating mixer do? It flips between 0^O and 180^O as a sort of simulation of rotation, but it could be thought to be rotating either clockwise or anti-clockwise, so you get both sum and difference frequencies out. If you want to read further, try the RF mixer in "SSB: third method, fourth explanation" Electronics World + Wireless World" April 1993 pp278-284.

Is coming soon.

Is coming soon.

©Nic Hamilton 2003