![]()
![]()
Étude précise de l'erreur de surface
L'erreur de surface du réflecteur est un contributeur très important de
l'efficacité globale de l'antenne, du même ordre que la contribution liée à
illumination par la
source (spill over, blocage etc..). L'erreur
![]() représente la valeur rms
de l'erreur de surface définie comme la déviation par rapport au paraboloïde
parfait. Ce paraboloïde parfait est celui qui approxime le mieux la surface
réelle c'est dire qui minimise l'erreur moyenne.
représente la valeur rms
de l'erreur de surface définie comme la déviation par rapport au paraboloïde
parfait. Ce paraboloïde parfait est celui qui approxime le mieux la surface
réelle c'est dire qui minimise l'erreur moyenne.
![]() ne prend pas ici en
compte la distribution réelle de l'erreur le long de la surface, celle ci est
supposée comme ayant une distribution gaussienne, ce qui est acceptable dans la
réalité pour des erreurs rms ne dépassant pas le lambda/20. En effet la
périodicité de l'erreur ne joue presque plus en dessous de lambda/20.
ne prend pas ici en
compte la distribution réelle de l'erreur le long de la surface, celle ci est
supposée comme ayant une distribution gaussienne, ce qui est acceptable dans la
réalité pour des erreurs rms ne dépassant pas le lambda/20. En effet la
périodicité de l'erreur ne joue presque plus en dessous de lambda/20.
Nous nous plaçons donc implicitement dans le cas d'une erreur rms au moins aussi bonne que lambda/20, choix justifié par la suite.
Pour un réflecteur imparfait, le gain va d'abord croître au carré de la
fréquence puis atteindre un maximum pour ensuite diminuer à cause de
l'imprécision de surface. La relation suivante donne la longueur d'onde du
maximum de gain de l'antenne, c'est à dire en fait la longueur d'onde minimale
(ou la fréquence maximale) utilisable pour le réflecteur ayant une erreur de
surface rms ![]() :
:
![]()
![]() avec
fmax en GHz et l'erreur rms en cm.
avec
fmax en GHz et l'erreur rms en cm.
Exemple : erreur
![]() de 1cm : fmax = 2,4 GHz
de 1cm : fmax = 2,4 GHz
Bien entendu à cette fréquence la pénalité de gain est très importante.
Il faut se fixer une pénalité de gain acceptable à la fréquence d'utilisation. Les différents graphes montrent qu'il est nécessaire de viser une erreur rms de lambda/20 pour rester dans le dB de pénalité.
Dans ces conditions fmax = 1,6 futile.
Exemple : futile = 2,4GHz
alors : ![]() = 6mm et fmax =
3,8 GHz
= 6mm et fmax =
3,8 GHz
Dans notre design géodésique, l'erreur de surface provient de la forme qu'épouse le grillage lorsqu'il est étiré sur cette structure géodésique. Plus précisément l'erreur est maximale au centre de chaque triangle du maillage et minimale sur les bords car nous savons que par construction les bords du triangle sont très proche de la surface parabolique aux erreurs négligeables près.
Par le fait de son élasticité le grillage tend à minimiser sa surface. Ainsi la surface obtenue est ce que l'on appelle "une surface minimale". C'est la même surface ou membrane que l'on obtiendrait si l'on plongeait le maillage dans de l'eau savonneuse (à la manière de faire des bulles)!
L'étude de ces membranes est, une fois de plus, tout un domaine de la physique et des mathématiques et peut s'avérer fort complexe. Ainsi pour calculer l'erreur de surface de la parabole il faudrait en toute rigueur calculer ces surfaces minimales. Mais ici le but n'est pas de plonger dans la théorie mais de chercher à interpréter de façon qualitative et réaliser des approximations qui ont un sens et permettant de simplifier certains calculs, à l'instar du calcul des géodésiques.
Ce type d'erreur de surface est analogue aux erreurs dites de "facettage" c'est à dire aux erreurs systématiques qui sont causées par l'emploi d'un assemblage de facettes pour approcher une surface lisse.
Intéressons nous aux erreurs de facettage sur une surface parabolique. Le dessin suivant illustre deux types de facettes possibles utilisées classiquement dans la réalisation des structures: un maillage à base de triangles et un maillage à base d'hexagones. A noter que ces maillages ne sont pas nécessairement géodésiques.
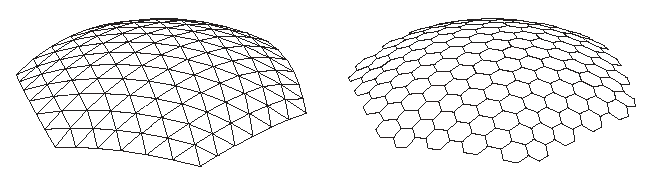
Deux formes de facettage
Le type de facettage triangulaire illustré ci dessus est celui utilisé par la technologie AstroMeshTM: des câbles sont disposés et tendus afin de former des facettes triangulaires servant de support au grillage. Des études très sérieuses ont été menées sur ces structures pour calculer les erreurs de surface résultantes. Un rapport de thèse très intéressante résume les conclusions de ces études: "Deployable Tensegrity Structures for Space Applications" de Gunnar Tibert (Stockholm, 2002, Royal Institute of Technology, Department of Mechanics). Voici les extraits qui nous intéressent:
- le paramètre à calculer est
l'erreur de surface rms sur toute la structure notée
![]()
- des formules approchées de l'erreur RMS sont données dans la littérature. Elles se basent sur une approximation sphérique de la surface parabolique (sphère de rayon 2xfocale). Cette approximation a été validée dans la pratique. Elles se basent aussi sur l'approximation de triangles équilatéraux ce qui est tout à fait raisonnable dans la pratique à partir d'une certaine finesse de maillage. A cet égard le maillage "JA6XKQ" est un peu "limite" sur cette approximation.
- il est aussi montré que la facette triangulaire est la mieux adaptée au maillage du réflecteur parabolique par rapport aux facettes carrées ou hexagonales.
La formule suivante donne l'erreur rms pour un maillage composé de triangles équilatéraux plats de cotés l et pour un réflecteur de focale F et de diamètre D:
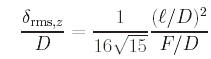
La formule suivante donne l'erreur rms pour un grillage reposant et tendu cette fois-ci sur des triangles équilatéraux courbes dont les cotés ont un rayon de courbure de 2.F (dirigé vers l'axe du réflecteur ou encore vers le centre de la sphère modèle):
![]()
soit 49% plus faible que précédemment.
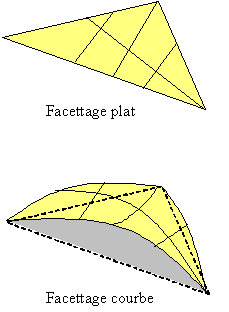
Vu toutes les hypothèses prises précédemment, nous pouvons dire que ces formules sont applicables à notre design géodésique. La première représente un pire cas alors que la deuxième représente un meilleur cas. Raisonnablement nous pouvons utiliser la moyenne des deux formules ce qui nous amène à:
![]()
Ainsi la longueur minimale d'un arc géodésique formant un coté d'un triangle pour une erreur rms donnée est :
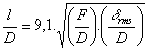
Cette formule permet donc de pré dimensionner la densité du maillage géodésique nécessaire pour une erreur de surface rms donnée, cette dernière dépendant de la pénalité de gain et de la fréquence d'utilisation recherchées.
Exemple appliqué à la parabole de JA6XKQ de 90cm:
Recherchons une erreur rms de lambda/20 à 2,4GHz soit 6mm. Le calcul donne:
| D (m) | 0,9 |
| F/D | 0,35 |
| delta rms (m) | 0,006 |
| l (m) | 0,395 |
Il faut donc des triangles géodésiques de coté maximal 395 mm. Si nous reprenons les cotes nous voyons que le coté le plus long (L2) est de 320 mm. Ainsi lambda/20 est acquis soit une dégradation de gain ne devant pas dépasser 0,7 dB.
Comparaison avec le maillage en étoile
Dans le même rapport de thèse nous trouvons avec grand intérêt la formule approchée donnant l'erreur de surface rms pour une parabole conçue avec un maillage en étoile, c'est à dire le design classique des bras convergents (ou "parapluie"):

avec l l'écart entre deux bras successifs à la périphérie du réflecteur.
l se calcul alors par :
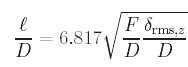
Reprenons l'exemple précédent. On aurait alors l = 295 mm ce qui représente environ 9 bras.
On retrouve en effet le nombre de bras typiquement utilisés : 10, 12 ...
L'effet des lattes sur la précision de surface
Technologiquement l'utilisation de lattes souples pour réaliser le maillage apporte certains effets parasites qui sont:
- l'effet de superposition des épaisseurs des lattes aux noeuds du maillage. Pour des lattes de 2mm d'épaisseur cela entraîne une épaisseur totale de 6mm soit une erreur de plus ou moins 3mm.
- la courbure élastique naturelle des lattes n'épouse pas parfaitement une forme parabolique.
Dans la réalité les erreurs ainsi engendrées sont mineures. Sur 2,4GHz elles représentent des erreurs de l'ordre de lambda/40 à lambda/35.
La dernière mise à jour de cette page date du mardi 08 décembre 2015