![]()
![]()
Le principe
Toute mon expérimentation tire son origine de l'idée originale de JA6XKQ d'utiliser les structures géodésiques pour réaliser des réflecteurs paraboliques. L'utilisation de telles structures géodésiques n'est pas une idée nouvelle puisqu'elles sont largement répandues en architecture dans la construction des dômes, mais aussi pour construire des radomes ainsi que des paraboles professionnelles de toutes tailles.
C'est l'architecte américain Buckminster Fuller qui est le père de toutes ces structures géodésiques et de tout le courant de pensé alternatif parallèle. Son oeuvre la plus connue est la Biosphère à Montréal au Québec. Pour l'avoir vue je peux témoigner que l'ouvrage est impressionnant!
C'est tout simplement extraordinaire de constater avec quelle simplicité et quelle légèreté il est possible d'obtenir de telles structures de dimensions aussi imposantes. "Avec presque rien, il est possible de faire presque tout", et pour Buckminster Fuller le triangle était la forme de base idéale à toute construction. A l'époque (années 60) ce type de construction géodésique a marqué une véritable révolution. En plus des qualités architecturales, des qualités écologiques ont été démontrées surtout en terme d'économie d'énergie, d'ou à cette époque une prolifération de maisons rondes, modulaires, construites à base de maillage géodésique.
 La Biosphère |
 Géode de la Citée des Sciences et de l'Industrie |
|
Un radome |
Une maison géodésique |
|
Design CAO d'un maillage géodésique de parabole réalisé avec Windome |
 Réalisation de réflecteurs paraboliques de grands diamètres pour applications spatiales. AstroMeshTM. |
Radiotélescope de Dwingeloo (Pays Bas) de 23m de diamètre. |
Le principe géodésique appliqué à la réalisation de nos paraboles apporte des bénéfices principalement sur les deux aspects suivants:
- maîtrise de la précision de surface
- facilité et avantages dans la fabrication
Un maillage triangulaire favorable à la précision de surface
Pour garder de bonnes performances en montant en fréquence il faut savoir réaliser un réflecteur avec précision, c'est à dire avec le minimum d'erreur de déviation par rapport à une surface parabolique parfaite. Traditionnellement on considère que la précision nécessaire est de l'ordre de lambda/10 au minimum et, mieux, de lambda/20. Cependant, ces "lambda/20" renferment plus de subtilités que l'on peut croire. En effet il faut tenir compte non pas seulement de la valeur maximale de l'erreur de la surface mais aussi de la distribution de cette erreur sur la surface. Un paramètre important est la périodicité de l'erreur le long de l'axe du paraboloïde en s'éloignant du centre.
La figure suivante du VHF/UHF Manual (RSGB) montre comment cette distribution intervient exactement.
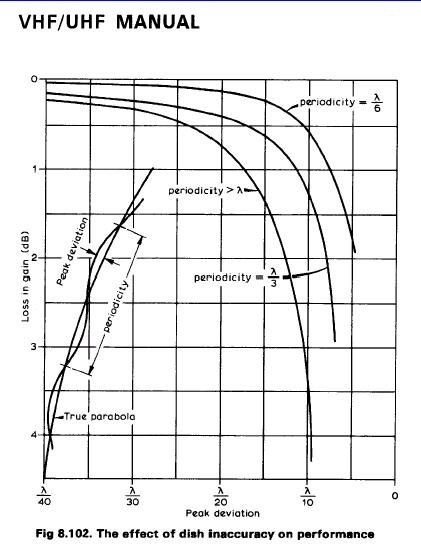 Source : RSGB VHF/UHF Manual |
Source : ARRL Antenna Book |
Prenons une erreur de déviation crête de lambda/10. Si la périodicité de l'erreur est de lambda alors la pénalité sur le gain est de 3dB !
Par contre, si elle peut être réduite à lambda/6 alors la pénalité n'est plus que de 0.5dB ! Ce qui est négligeable.
Nous voyons donc immédiatement l'intérêt de fabriquer une structure de réflecteur avec un maillage distribué de façon homogène.
Justement, le maillage géodésique le permet car chaque point de maille couvre de façon homogène le réflecteur. Chaque point de maille est exactement un point de paraboloïde par construction, ainsi la périodicité spatiale de l'erreur de surface se trouve considérablement réduite par rapport à d'autres structures employées, en particulier celles utilisant classiquement le maillage en étoile.
| Maillage en étoile (design classique)
|
Maillage triangulaire (design
géodésique)
|
Ainsi le maillage géodésique est favorable vis à vis de la pénalité de gain liée à l'erreur de surface car elle permet un répartition plus homogène des erreurs de surface.
Cette remarque est générale. Nous voyons d'après les courbes de la figure que le bénéfice est réel pour des erreurs crêtes de plus de lambda/20 et pour une périodicité d'erreur de lambda/3. Sur 2400MHz une telle périodicité correspond à 13cm/3 = 4cm, ce qui commence à représenter un maillage très dense! Il faut donc tempérer nos conclusions.
En conclusion, nous pouvons dire qu'un maillage géodésique permet de maîtriser bien mieux la surface parabolique par rapport à un maillage en étoile car elle s'obtient de façon "spontanée" et naturelle avec une précision mathématique. De plus le maillage triangulaire donne une une répartition des erreurs plus homogène que la structure étoilée. Ces deux aspects ne peuvent être que bénéfiques sur le gain. Enfin la reproductibilité des performances est assurée.
Une grande facilité de réalisation
Les courbes géodésiques ont des propriétés mécaniques très intéressantes. Ce sont en particulier les courbes tracées sur la surface à courbure géodésique nulle : de façon imagée, ce sont les trajectoires d'observateurs se déplaçant sur la surface en marchant droit devant eux, ou de petites voitures dont la direction est bloquée en position rectiligne.
Cela a un impact très intéressant sur le plan technologique : en déroulant à partir d'un point A une latte de faible largeur par rapport à la courbure de la surface et rejoignant B à l'arrivée nous obtenons une géodésique entre A et B. Autrement dit nous avons les points suivants fondamentaux de notre design:
- le maillage géodésique peut être réalisé à partir de lattes plates, droites et souples
- la surface de la latte reste tangente à la surface
- aux points de croisement des mailles les lattes sont tangentes (elles s'appliquent l'une sur l'autre)
Nous voyons donc immédiatement l'intérêt du design:
- la réalisation se limite à un perçage et à un assemblage de lattes souples en profitant de leur élasticité naturelle. La forme parabolique naît d'elle-même au cours de l'assemblage!
- aucun ajustement nécessaire une fois que le maillage est réalisé. La précision de la surface est garantie par la précision du perçage des lattes, c'est tout!
Enfin, un autre point très important est la pose du grillage. C'est en général le plus pénible dans la réalisation des réflecteurs car fastidieux surtout lorsque le grillage est assez rigide et tend de se fait à gondoler. Avec le design géodésique nous réalisons une structure maillée qui permet la pose du grillage DERRIÈRE le réflecteur. Le grillage se pose alors comme une peau que l'on peut étirer facilement et qui évite les faux plis.
Une structure rigide
L'autre propriété intéressante de ce maillage est sa rigidité. En architecture de nombreux dômes et radomes sont fabriqués en utilisant un maillage géodésique car il offre une grande résistance aux efforts mécaniques surtout ceux liés à la gravité en répartissant les efforts.
Dans notre approche, les lattes sont courbées de part leur élasticité, de ce fait toute la structure est en tension mécanique. Le maillage triangulaire répartit les forces mécaniques dans toutes les directions. Pour un diamètre de 1m aucune structure de renfort n'est nécessaire, ce qui allège considérablement la structure. Pour des diamètres plus importants, des éléments rigides doivent être utilisés, mais leur nombre est toujours réduit au minimum.
Résumé des avantages de la construction géodésique
| Critères | Construction géodésique | Construction à base de bras paraboliques rigides (maillage étoile) |
| Facilité de fabrication des éléments de structure | Très facile, ne nécessite que des lattes plates souples en aluminium qu'il faut couper et percer | Chaque bras doit être fabriqué à l'identique mais demande un certain travail car la forme doit être la plus proche possible d'une parabole et rigide. Cela entraîne en générale une structure avec bras de renforts donc pas mal de découpe, perçage, rivetage, avec des profilés de tailles différentes etc...... |
| Facilité d'assemblage des éléments de la structure | Très facile, ne demande aucun ajustement mécanique. Il faut juste relier chaque noeud avec une vis et un écrou ou un rivet et la forme parabolique apparaît d'elle même! | L'assemblage de tous les bras demande un contrôle mécanique précis afin qu'ils soient tous bien positionnés, sinon cela entraîne une imprécision importante de la surface. Enfin pour les diamètres important un cerclage intermédiaire est utile. |
| Nombre d'éléments de structure | Idem | Idem |
| Précision de la surface | Ne dépend que de la précision du perçage initial et de la souplesse des lattes. Répartition homogène des erreurs sur la surface. | Dépend de la précision de la courbe de chaque bras et de leur fixation à la base. La répartition des erreurs n'est pas homogène car la distance entre les bras augmente au fur et à mesure que l'on s'éloigne du centre du réflecteur. |
| Robustesse | Robuste | Très robuste |
| Poids | Léger | Peu augmenter très vite avec la complexité de la structure des bras |
| Pose du grillage | Facilité par l'homogénéité de la structure géodésique. Se pose en étirant derrière la structure. | Délicate entre les bras surtout lorsque l'on s'éloigne du centre! Le grillage ne peut se poser qu'au dessus de la structure (d'ou des plis etc..) |
| Temps de réalisation d'une structure de 1m de diamètre | Quelques heures | Plusieurs jours |
Les autres techniques de réalisation
| Types | Applications | Difficultés |
| Paraboles à réflecteur rigide réalisé
en un seul bloc ou en pétales: surface métallique conformée, surface en
résine obtenue après moulage Photo (F4BUC) |
Précision de surface très importante permettant une utilisation sur des fréquences très élevées (10GHz et plus ..) | Réalisation presque en dehors de porté de l'amateur |
| Assemblage de bras rigides de forme
paraboliques et fixés à la base du réflecteur. Complété par des anneaux
concentriques prenant appuis sur les bras. Un grillage prend appui sur les
bras et épouse alors la forme parabolique. Exemple : design OE9PMJ. Photo (WA8YKN) |
Typiquement dans le domaine amateur paraboles de diamètres allant jusqu'à 10m. Structure rigide et plus légère. Typiquement utilisé jusqu'à queqlues GHz pour les diamètres de qques mètres. | Réalisation et fixation des bras. Pose du grillage. |
| Assemblage de bras souples dont la
forme devient quasi-parabolique lorsqu'ils sont soumis à une flexion par des
haubans. Dans la littérature anglaise on parle de "stressed parabolic dish".
Exemple: design K2UYH
Photo (F2TU) |
Légère et bien adaptée au portable pour des diamètres jusqu'à 5m. Précision de surface moins bonne à moins de rigidifier les bras en rajoutant de la matière ou des haubans supplémentaires. Très bien pour une réalisation simple, peu coûteuse pour un diamètre de 4m et utilisable jusqu'à 1.2GHz. | Impossible de s'appuyer sur les bras pour tenir la source. Pose alors un problème sérieux de mécanique surtout pour une source de poids non négligeable |
| Parabole gonflable. Design original exploitant la propriété d'une surface élastique à acquérir une forme quasi-parabolique lorsqu'elle est soumise à une pression. | Des projets existent pour utiliser cette technologie pour le spatial. Le satellite SPARTAN utilise cette nouvelle technologie. | Maîtrise des matériaux nécessaires hors de portée de l'amateur. |
| Parabole géodésique | Beaucoup d'avantages à la réalisation et sur la maîtrise des performances. | La structure commence à se complexifier à partir de 2m de diamètre |
La dernière mise à jour de cette page date du mardi 15 décembre 2015

