![]()
![]()
La méthode de calcul des lignes géodésiques du réflecteur parabolique
L'étude des lignes géodésiques d'une surface est un domaine de recherche à part entière. Cela est justifié par exemple par leur rôle dans le domaine du traitement d'images.
La théorie des géodésiques n'est pas simple et sous forme généralisée elle aboutit vite à des équations analytiques difficiles voir dans certains cas impossibles à résoudre.
Nous allons ici exposer une méthode basée essentiellement sur de la géométrie évitant les calculs complexes.
Notre problème est ici le suivant : étant donné deux points A et B sur le même bord d'une surface parabolique (mêmes coordonnées z), déterminer la ligne géodésique reliant ces deux points.
Certaines surfaces ont l'avantage de présenter des solutions simples ne demandant aucun calcul complexe:
- les géodésiques du plan sont les segments de droites
- les géodésiques de la sphère sont des arcs de cercles
- les géodésiques du cylindre sont des hélices
... mais qu'en est-il pour le paraboloïde de révolution?
En fait il n'existe pas de solution analytique simple mais un système d'équations différentielles. Malgré les propriétés connues des lignes géodésiques des surfaces de révolutions (théorème de Clairaut etc..) il n'existe pas d'équations directes pour le paraboloïde. Afin de résoudre le problème, il existe alors principalement deux méthodes:
- une résolution algorithmique basée sur des calculs itératifs. Par exemple en utilisant l'algorithme du "fast marching"
- une méthode graphique approchée et basée sur un principe de projection
C'est cette deuxième méthode que nous allons utiliser.
La méthode de projection
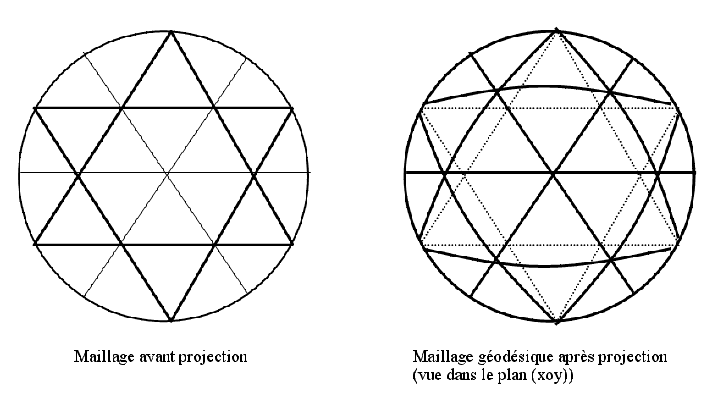
Les dômes géodésiques sont très souvent calculés par la méthode de projection. Il s'agit de projeter les points d'un polyèdre sur la surface du dôme à partir d'un point. Cette méthode est exacte pour les dômes sphériques, forme représentant du reste la majorité des dômes géodésiques. Dans ce cas il suffit de déterminer un polyèdre circonscrit dans la sphère, par exemple un icosaèdre. Chaque face de ce polyèdre est ensuite subdivisé en triangles, réalisant ainsi un maillage plus ou moins fin.
La projection du polyèdre maillé par rapport au centre de la sphère sur la sphère aboutit à un maillage géodésique exact de la sphère. En effet un segment AB du maillage du polyèdre se trouve projeté en un arc de cercle A'B' sur la surface sphérique c'est à dire en une géodésique.
Le principe de la méthode de calcul
Vous commencez sans doute à deviner est que nous allons essayer d'utiliser ce principe graphique de projection pour notre paraboloïde.
En fait il se trouve que pour un F/D pas trop faible (>0,3) nous pouvons réaliser une bonne approximation de la surface parabolique par une surface sphérique, et ceci parce que la forme du réflecteur est en fait assez peu "creusée".

Exemple d'approximation parabole/cercle
Prenons les deux points A et B sur la surface parabolique et utilisons une sphère dont le centre est situé sur l'axe du paraboloïde et le rayon pris tel que A et B appartiennent aussi à la sphère.
Réalisons le projection sur la sphère du segment AB pour tracer la géodésique de la sphère entre A et B.
Réalisons la même projection cette fois-ci sur le paraboloïde.
Vu la faible distance entre la surface sphérique et le paraboloïde la géodésique de la sphère et la projection sur le paraboloïde sont très proches. Il est aussi tout à fait instinctif d'imaginer que de ce fait le plus court chemin entre A et B sur le paraboloïde doit être très proche de cette courbe. Nous pouvons donc dire qu'une première approximation de la géodésique du paraboloïde entre A et B est la projection du segment AB sur ce dernier à partir du centre de la sphère modèle.
Maintenant il est possible d'améliorer cette approximation en déterminant plus finement le centre de la projection. Pour cela on le choisit tel que le projeté C' du centre C du segment AB rende la droite CC' normale à la surface du paraboloïde en C'. En effet on peut imaginer une approximation de la géodésique par les deux segments AC' + C'B. On voit bien qu'en promenant C' le long du méridien la longueur totale AC' + C'B sera minimale lorsque CC' sera normal à la surface.
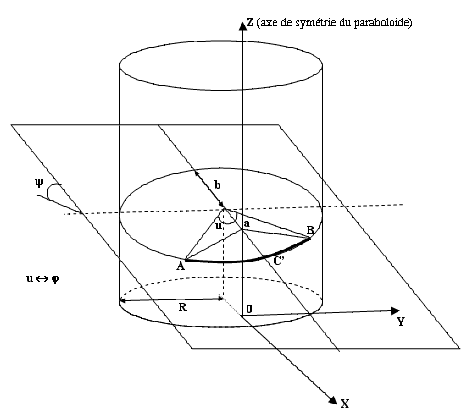
Le calcul graphique de notre géodésique revient alors à projeter le segment AB sur la surface du paraboloïde à partir d'un point noté a situé sur l'axe OZ (axe de symétrie de révolution).

Dessins ©F4BUC
Cela est graphiquement la même chose que l'intersection du plan contenant a,A et B avec la surface du paraboloïde.
Beaucoup d'approximations certes, mais aussi beaucoup de bon sens. Avec cette méthode je retrouve exactement les cotes de JA6XKQ pour tous les F/D.
Les étapes de calcul
Pour pouvoir calculer les cotes pour la réalisation du maillage géodésique nous devons déterminer la longueur de l'arc géodésique et ses intersections avec les méridiens du paraboloïde.
Quelques équations très simples montrent que la courbe obtenue dans le plan (xoy) de l'intersection d'un plan avec un paraboloïde est un arc de cercle. Ainsi cela est équivalent à l'intersection d'un cylindre avec un plan.
Il est bien connu que l'intersection d'un plan avec un cylindre donne une ellipse sur le plan.
Au final, notre calcul de géodésique est en réalité un calcul d'arc d'ellipse!
Le calcul se décompose selon les étapes suivantes:
- déterminer a, le centre de la projection
- déterminer le centre et le rayon du cylindre
- déterminer les paramètres de l'ellipse
- calculer les longueurs d'arcs de l'ellipse selon le fractionnement initial de AB
- calculer les longueurs d'arcs de méridiens
Dessins ©F4BUC
On calcul au final toutes les cotes fournies par JA6XKQ (A1, A2 ...) et permettant le perçage des lattes et donc leur assemblage (simplissime).
Les résultats de mes calculs donnent exactement les cotes fournies par JA6XKQ pour les différents f/d au mm près, ce qui est rassurant. Il est à noter que la précision de cette méthode se réduit pour des F/D faibles, c'est à dire pour des paraboles plus creuses, mais je n'ai pas investigué en détail ces limitations.
Ainsi il m'est possible de calculer d'autres maillages géodésiques du paraboloïde et donc de concevoir des réflecteurs paraboliques utilisant d'autres formes de maillages.
Le prototype de 1m80 est un exemple ou le sous maillage a été calculé avec cette méthode.
La dernière mise à jour de cette page date du mardi 08 décembre 2015