????????....

by James Miller G3RUH

INTRODUCTION

In December 1983 OSCAR NEWS published my program listing "OSCAR10.BAS" [1]. In heavily commented style it documented the basic routines one needs to build up a satellite tracking program. It must have been popular, since for some while it was the most requested back issue of O.N., and has formed the basis of many other authors' software (for example SATSCAN, VECSAT and parts of RealTrak for the IBM-PC, !ArcTrack for the Archimedes, the SATTRACK III Antenna/Radio Controller and numerous private programs).

In time the program accumulated several other modules, with the mathematics described in interim O.N. articles. When issued for the BBC micro the program acquired the name "PLAN10", and later "PLAN13", and it's been transcribed for several other machines including the IBM-PC and Commodore 64 etc.

In recent years or so my mail has featured more and more queries about tracking matters than was usual. The flavour of these suggests that a new generation of satellite enthusiasts is emerging and are rightly asking the old questions anew.

So for a long while I've been intending to re-publish these routines, but in their most up-to-date embodiment. Hence this pamphlet. I don't intend to provide 100% mathematical details. To do so means essentially writing the whole program out anyway, and references are plentiful.

Old hands will recognise the coding style. Additions include the Sun's position, eclipses, visibility, Sun angle, sub-satellite point, mode switching, date algorithms and direct range-rate calculations for doppler shift.

Almost every publication to do with satellites has information about orbits and their properties. For general reading "THE SATELLITE EXPERIMENTER'S HANDBOOK" [2] is unsurpassed, and itself documents several hundred references. "FUNDAMENTALS OF ASTRODYNAMICS" [3] is a no-nonsense text that's full of insights, and is incredibly cheap.

"MODELS FOR THE PROPAGATION OF Norad ELEMENT SETS" [4] documents five ways to use a set of keps properly. SGP, the simplest model, runs to 4 pages of higher mathematics just to compute satellite position and velocity. All amateur implementations (i.e. lines 2000-2210 of PROCsatvec) use only the first half page of this, skipping the long term perturbatory effects. "SUN'S UP" [5] is about modelling the Sun's position, and describes applications including illumination and eclipses. "30.6 DAYS HATH SEPTEMBER" [6] documents date algorithms. "THE ASTRONOMICAL ALMANAC" [7] is invaluable for checking calculations; an annual, but useful for many years.

Surprisingly when OSCAR10.BAS was published there were complaints that "filling Oscar News with programs was a waste of space" etc etc. My reply to this myopic view was, and remains:"The program was designed to be more than a mere listing to be blindly typed in and run. It is a treatise giving all the equations for solving the elliptic orbit and related problems. To do this, as well as provide a tool suitable for immediate use the program was written in a quasi-algebraic style. Variable names were chosen to be meaningful, there are copious comments, and routines are written so that users can adapt them as they wish. However the published arrangement is not the only one. The program is a clear formulation of the general satellite orbit problem, and is sure to provide the interested amateur with several months of absorbing self-training material". Plunder! Enjoy!

SATELLITE POSITION CALCULATIONS

FORMULAE:

The function of ANY satellite tracking program is to calculate these basic quantities.

Range: R = S - O |R|^2 = R . R r = R/|R|

~ ~ ~ ~ ~ ~ ~

Az and El: El = ASN( r.u ) Az = ATN( r.e / r.n )

. ~ ~ . . ~ ~ ~ ~

Range Rate: |R| = r . (S - O)

~ ~ ~

Squint: sq = ACS ( -r.a) ] For Oscar-10 and

~ ~ ] Oscar-13 type

Sun angle: sa = ASN ( -a.h ) ] satellites

~ ~

Eclipse: c = -h.s ; IF c > 0 AND |S|*(1-c*c)^.5 < Re THEN "ecl"

~ ~

Visibility: IF ASN(h.u) < -10 deg AND NOT"ecl" AND El > 0 THEN "vis"

~ ~

SYMBOLS: .

S = satellite's position vector S = satellite's velocity vector

~ ~.

O = observer's position vector O = observer's velocity vector

~ ~

R = range vector from observer to satellite

~ .

|R| = range magnitude |R| = range rate

r = unit vector in direction of range

~

u, e, n = unit vectors, observer's local directions Up, East, North

~ ~ ~

a = unit vector in direction of satellite antenna axis

~

h = unit vector in Sun's direction ("h" for helios)

~

s = unit vector in satellite's direction

~

|S| = satellite's distance from Earth Re = Earth's radius

VECTORS

Manipulations use vectors throughout. While spherical trigonometry could also be used, it tends to be very clumsy and invariably obscures the mechanics. Angles are fine for human oriented input/output, but in 3 dimensional analyses, vectors have no equal. In the satellite position problem vectors are used to represent distances, directions and velocities, AND ARE UNDERLINED. All have 3 components. They may be added or subtracted provided they are in the same units, and may also be multiplied. The golden rule is that any vectors so combined MUST be specified in the same coordinate system. In fact much of any satellite calculation program is concerned with ensuring just that.

A denotes a 3-D vector, components {Ax, Ay, Az}.

~

A.B denotes the "dot" product: A.B = B.A = Ax*Bx + Ay*By + Az*Bz

~ ~ ~ ~ ~ ~

If a and b are unit vectors, a.b = COS (angle between a and b)

~ ~ ~ ~ ~ ~

Fig 1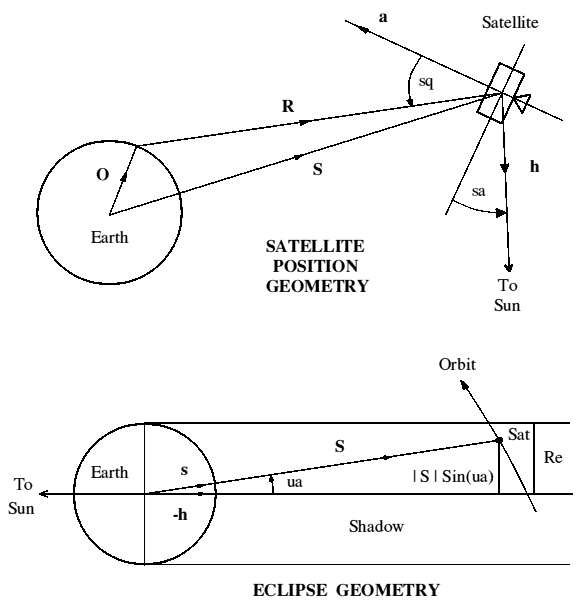

OUTLINE OF PROGRAM

The program consists of a small collection of routines; to invoke their use there is a simple driver at lines 10-280. It produces an output like:

PLAN13 v2.0 SATELLITE PREDICTIONS

-----------------------------------

Enter start date (e.g. 1990, 12, 25) ? 1990,11,3

Enter number of days for printout ? 1

OSCAR-13 - G3RUH AMSAT DAY 4689 1990 Nov 3 [Sat]

ORBIT: 1828 AP/RAAN: 239/128 ALON/ALAT: 180/0 SAZ/SEL: 210/-72 ILL: 96%

UTC MA MODE RANGE EL AZ SQ RR ECL? HGT SLAT SLON

-----------------------------------------------------------------------------

0100 38 B 25929 3 89 48 2.1 vis 20635 13 80

0115 43 B 27716 8 87 43 1.9 vis 22880 17 79

0130 49 B 29345 12 86 38 1.7 vis 24917 21 78

0145 55 B 30825 16 85 34 1.6 vis 26763 24 77

Amsat day numbers are reckoned from 0 = 1978 Jan 01; AP is argument of perigee; ALON/ALAT are the satellite's attitude; SAZ/SEL are Sun's position in the orbit plane, and ILL is solar panel illumination. MA is mean anomaly in units of 256 per orbit. SQ is squint angle, RR is range rate (km/s), ECL? will indicate if the satellite is in eclipse, or whether it is potentially visible. HGT is height (km), and SLAT SLON are sub-satellite latitude and longitude (deg East).

PROGRAM NOTES

After initialisation ("init") the program prompts you for a start date and duration of run, then sets up day, hour and minute loops to call the routines "satvec", "rangevec", "sunvec" and "printdata".

PROCinit (lines 1000-1840): All the constants needed by the routines are established here. Most relate to a physical quantity, but are then combined with others or need units changing to form a derived quantity. Some of these constants are only used transiently within "init" itself, but are included for clarity.

PROCsatvec (lines 2000-2430): Takes input variables day (DN) and fraction of day (TN) and computes satellite position, velocity and antenna direction in orbit plane coordinates. These are then output in celestial coordinates and geocentric coordinates.

PROCrangevec (lines 4000-4200): Calculates Range vector from satellite and observer vector, and derives range, azimuth, elevation, squint, range rate and sub-satellite point.

PROCsunvec (lines 3000-3260): Computes Sun's position in celestial coordinates, and then Sun angle, illumination, visibility and eclipse details. Actual visibility also depends on brightness of satellite, and darkness of sky.

FNday(Y,M,D) Function returns a general day number from year, month and day. Value is Julian Day - 1721409.5 or Amsat day + 722100

FNdate(DN) Function converts day number to a string, e.g. 1990 Nov 3 [Sat]

FNatn(Y,X) Crash-proof four quadrant arctangent. Returns value in range 0-2pi

CONVERSION NOTES

BBC BASIC Effect OTHER BASICS

----------------------------------------------------------------------

PROCname .... ENDPROC subroutine GOSUB nnnn .... RETURN

DEG(X) rad -> deg X*180/PI ) where PI =

RAD(X) deg -> rad X*PI/180 ) 3.141592654

ASN(X) arcsin FNatn(X,SQR(1-X*X))

ACS(X) arccos PI/2 - FNatn(X,SQR(1-X*X))

----------------------------------------------------------------------

COORDINATE SYSTEMS

A number of rectangular 3-D XYZ coordinate systems are used in the program,viz: Celestial, Geocentric, Orbit plane.

Definitions:

CELESTIAL: System fixed with respect to the stars. XY plane coincident withEarth's equator. Origin: centre of the Earth.

X: Directed towards the First point in Aries (Right Ascension = 0)

Y: 90 degrees East around the equator (RA = 90)

Z: Directed towards the North pole

GEOCENTRIC: System as celestial, but fixed to the Earth; related via Greenwich Hour Angle Aries (GHAA). Origin: centre of the Earth.

X: Directed to intersection of Equator and Greenwich meridian (Longitude = 0)

Y: 90 degrees East around the Earth's Equator (Longitude = 90E)

Z: Directed towards the North pole

ORBIT PLANE: Fixed (almost) with respect to the stars, in orientation defined by argument of perigee, inclination and RAAN. Origin: Earth's centre.

X: Directed towards perigee

Y: 90 degrees from perigee round the orbit in direction of satellite's motion

Z: Perpendicular to orbit plane

ADDITIONAL NOTES

ORBIT PLANE -> CELESTIAL COORDINATE TRANSFORMATION

In earlier versions of the program, the conversion of a vector from Orbit plane coordinates to Celestial coordinates was written out stage by stage. That is, a rotation in argument of perigee, followed by a rotation through inclination, and finally through RAAN. Since there are actually several vectors (satellite position, velocity and antenna axis) to transform, this became a little clumsy, so the three rotations are now amalgamated into one. The array [C] that does this is computed at lines 2260-2290.

CELESTIAL -> ORBIT PLANE COORDINATE TRANSFORMATION

The array [C] can also be used in the reverse direction, to convert a vector from Celestial to Orbit plane coordinates. This is done by "transposing the array", using C(J,I) for C(I,J) throughout. This is used to calculate the Sun's position as seen from the orbit plane (lines 3210-3240).

DECAY

The Keplerian element DECAY is half the rate of change of mean motion. DECAY is usually very small, of order 10^-7, and its short term influence is small. For example, MA is affected by an amount DECAY*T*T over T days. Over 100 days that makes 10^-7*100*100 = 0.001 revolutions, or about 7.2 seconds for a 2 hour period satellite.

Decay is only really significant for low altitude satellites such as the space shuttle, MIR, or satellites nearing burn-up. Then the value can be as large as 10^-4. This causes in addition a noticeable second order effect on semi-major axis, argument of perigee and RAAN. The program accounts for this with terms calculated at line 2030.

For many purposes, especially if the Keplerian elements are regularly updated, drag can be ignored. This is true in particular for Oscar-13, where the unmodelled luni-solar perturbations are substantially larger than "decay".

DOPPLER SHIFT

The program calculates range-rate (line 4190) in km/s. If a satellite transmits a frequency FT, then this is received as a frequency FR: FR = FT * (1 - RR/299792). Note: 299792 is the speed of light in km/s

Thus the "doppler shift" FD is given by: FD = -FT*RR/299792.

The calculation of range-rate is accurate in vacuo. However, at low elevations the radio path through the Earth's atmosphere is not perfectly straight. This refraction causes the actual observed doppler shift at AOS and LOS to be as much as 1 part in 10^7 in error, say 50-100 Hz at 435 MHz. It should also be noted that simple crystal oscillators have a similar order of stability, and satellites usually experience large temperature changes.

FOOTPRINT

In some programs there is a requirement to draw a circle around the sub-satellite point to indicate the field of view of the satellite. The following routine indicates how to do this. It is coded for clarity, not for speed. It would be better to store SIN(A) and COS(A) in a table rather than compute them every call. Since the footprint is left-right symmetric, only one half of the circle's points need be computed, and the other half can be inferred logically.

The sub-routine's output is a unit vector {X,Y,Z} in geocentric coordinates for the I'th point on the Earth's surface. This will then need transforming to map coordinates (mercator, spherical, linear or whatever), and then screen coordinates to suit the computer.

DEF PROCfoot(RS, slat, slon)

REM Take satellite distance, sub-satellite lat/lon and compute unit vectors'

REM x,y,z of N points of footprint on Earth's surface in Geocentric

REM Coordinates. Also terrestrial latitude and longitude of points.

srad = ACS(RE/RS): REM Radius of footprint circle

cla = COS(slat): sla = SIN(slat): REM Sin/Cos these to save time

clo = COS(slon): slo = SIN(slon)

sra = SIN(srad): cra = COS(srad)

FOR I = 0 TO N: REM N points to the circle

A = 2*PI*I/N: REM Angle around the circle

X = cra: REM Circle of points centred on Lat=0, Lon=0

Y = sra*SIN(A): REM assuming Earth's radius = 1

Z = sra*COS(A) REM [ However, use a table for SIN(.) COS(.) ]

x = X*cla - Z*sla: REM Rotate point "up" by latitude slat

y = Y

z = X*sla + Z*cla

X = x*clo - y*slo: REM Rotate point "around" through longitude slon

Y = x*slo + y*clo

Z = z

LON(I) = FNatn(Y,X): REM Convert point to Lat/Lon (or as required by map

LAT(I) = ASN(Z): REM projection and display system).

NEXT I

ENDPROC

SQUINT ANGLE

Squint (or pointing) angle is the angle between the spacecraft's antenna and the observer. This is calculated at line 4120 for Oscar-13's high-gain antennas. As the low gain antennas are simple monopoles radiating normal to the <a> axis, low-gain squint is given by: SQ_low_gain = 90 - SQ_high_gain (deg)

Some satellites are stabilised so that they are continuously Earth pointing (e.g. UOSATs, P3D). For these, the antenna axis unit vector is aligned with the spacecraft's position vector, i.e. <a> = <-s> So to calculate the squintangle for these satellites use the formula:4120 SQ = DEG(ACS( (Sx*Rx + Sy*Ry + SZ*Rz)/RS )) (deg)

SUN MODEL and SIDEREAL CONSTANTS

The calculations of Earth rotation and Sun position are the most accurate part of this program! There is no need to update the solar constants at lines 1400 and 1630-1660 for several decades.