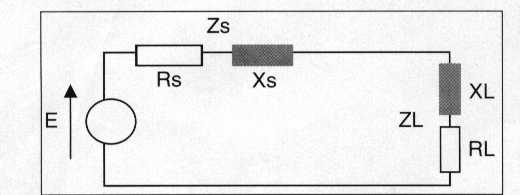
Rs + jXs = RL - jXL
"Going Around in Circles to Get to the Point"
Iulian Rosu, YO3DAC / VA3IUL, http://www.qsl.net/va3iul
Named after its inventor, Phillip H. Smith (Bell Laboratories), the Smith Chart was originally described in Electronics for January 1939. (Interview with Philip H. Smith)
Smith Chart it is a graphic tool for solving transmission lines problems.
One of the simpler applications is to determine the feed point impedance of an antenna, based on an impedance measurement at the input of an random length of transmission line.
The Smith Chart may be used for other proposes too, such as the design of impedance-matching networks. These matching networks can take on any of several forms, such as L and Pi networks, a stub matching system, a series-section match, and more.
Impedance matching is often necessary in the design of RF circuitry to provide the maximum possible transfer of the power between a source and its load. The source impedance must equal the complex conjugate of load impedance, or:
Rs + jXs = RL - jXL

The input impedance, or the impedance seen when “looking into” a length of line, is dependent upon the SWR, the length of the line, and the Zo of the line. The SWR, in turn, is dependent upon the load, which terminates the line. There are complex mathematical relationships which may be used to calculator the various values of impedances, voltages, currents, and SWR values that exist in the operation of particular transmission line.
The Smith Chart is developed by examining the load where the impedance must be matched, and is really nothing more than a specialized graph. Consider it as having curved, rather than rectangular, coordinate lines. The coordinate system consists simply of two families of circles, the resistance family, and the reactance family. The resistance circles are centered on the resistance axis, which is the only straight line on the chart. They are all tangent to the outer circle at the right of the chart. Each circle is assigned a value of resistance, which is indicated by the point where the circle crosses the resistance axis. All points along any one circle have the same resistance value.
The values assigned to these circles vary from zero at the left of the chart to infinity at the right, and actually represent a ratio with respect to the impedance value assigned to the center point of the chart, indicated 1.0. This center point is called prime center. If prime center is assigned a value of 100 ohms, then 200 ohm resistance is represented by the 2.0 circle, 50 ohms by the 0.5 circle, 20 ohms by the 0.2 circle, and so on. If, instead, a value of 50 is assigned to prime center, the 2.0 circle now represents 100 ohms, the 0.5 circle 25 ohms, and the 0.2 circle 10 ohms. In each case, it may be seen that the value on the chart is determined by dividing the actual resistance by the number assigned to prime center. This is called a normalization process.
Reactance circles appear as curved lines on the chart because only segments of the complete circles are drawn. These circles are tangent to the resistance axis, which itself is a member of the reactance family (with a radius of infinity). The centers are displaced to the top or bottom on a line tangent to the right of the chart. The large outer circle bounding the coordinate portion of the chart is the reactance axis.
Each reactance circle segment is assigned a value of reactance, indicated near the point where the circle touches the reactance axis. All points along any one segment have the same reactance value. As with the resistance circles, the values assigned to each reactance circle are normalized with respect to the value assigned to prime center. Values to the top of the resistance axis are positive (inductive), and those to the bottom of the resistance axis are negative (capacitive).
When the resistance family and the reactance family of circles are combined, the coordinate system of the Smith Chart results. Complex impedances (R + jX) can be plotted on this coordinate system.
For better understanding let's give an example. Suppose we have an impedance consisting of 50 ohms resistance and 100 ohms inductive reactance (Z = 50 +j100). If we assign a value of 100 ohm to prime center, we normalize the above impedance by dividing each component of the impedance by 100 (Normalization must be used, in order to facilitate the plotting of larger impedances. Each impedance to be plotted is divided by a convenient number that will place the new normalized impedance near the center of the chart where increased accuracy in plotting is obtained). The normalized impedance is then 50/100 + j(100/100) =
0.5 + j1.0. This impedance is plotted on the Smith Chart at the intersection of 0.5 resistance circle and the +1.0 reactance circle.
Instead of assigning 100 ohms to prime center, we assign a value of 50 ohms. With this assignment, the 50 + j100 ohm is plotted at the intersection of the
50/50 = 1.0 resistance circle, and the 100/50 = 2.0 positive the same impedance value, 50 + j100 ohms. This example shows that the same impedance may be plotted at different points on the chart, depending upon the value assigned to prime center. But two plotted points cannot represent the same impedance in the same time.
Prime center is a point of special significance. It is customary when solving problems to assign the Zo value of the line to this point on the chart, 50 ohms for a 50 ohms line, for example. The center point of the chart now represents 50 + j0 ohms, a pure resistance equal to the characteristic impedance of the line, that it represents a perfect match, with no reflected power and with a 1.0 to 1 SWR.
When plotting impedances two cases can be. These are short circuits and open circuits. A true short circuit has zero resistance and zero reactance, or 0 + j0. This impedance is plotted at the left of the chart, at the intersection of the resistance and reactance axes. An open circuit has infinite resistance, and therefore is plotted at the right of the chart, at the intersection of resistance and reactance axes.
In other words the zero ohms circles (r = 0) is the largest one and the infinite resistor circle is reduced to one point at (1,0). There should be no negative resistance. If one (or more) should occur, we will be faced with possibility of oscillatory conditions.
It can be seen that all of the circles of one family will intersect all of the circles of the other family. Knowing the impedance, in form of: r + jx, the corresponding reflection coefficient can be determined. It is only necessary to find the intersection point of the two circles, corresponding to the values r and x.
The reverse operation is also possible. Knowing the reflection coefficient, find the two circles intersecting at that point and read the corresponding values r and x on the circles. The procedure for this is as follows:
- Determine the impedance as a spot on the Smith Chart
- Find the reflection coefficient Γ (Gamma) for the impedance.
The reflection coefficient is defined as the ratio between the reflected voltage wave and the incident voltage wave:Gamma = Vref / Vinc
- Having the characteristic impedance and Γ (Gamma), find the impedance
Any point on the Smith Chart represents a series combination of resistance and reactance of Z = R + jX.Thus , to locate the impedance Z = 1 +j1, you would find R = 1 constant resistance circle and follow until it crossed the X = 1 constant reactance circle. The junction of these two circles would then represent the needed impedance value)
- Convert the impedance to admittance.
The equivalent admittance of a plotted impedance value lies diametrically opposite the impedance point on the chart. In other words, an impedance plot and its corresponding admittance plot will lie on a straight line then passes through prime center, and each point will be the same distance from prime center (on the same SWR circle)
- Find the equivelent impedance.
- Find the components values for the wanted reflection coefficient
The third family of circles, which are not printed on the main chart, but are added during the process of solving problems, are SWR circles. Each circle represents a value of SWR, with every point on a given circle representing the same SWR. The SWR for a given circle may be determined directly from the chart coordinate system, by reading the resistance axis to the right prime center.
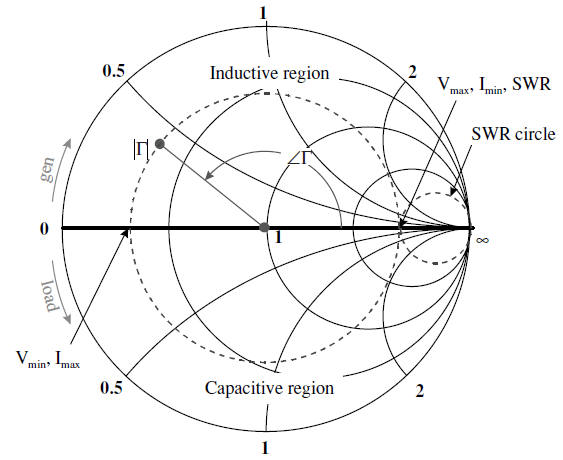
The Smith Chart has the following futures:
It represents all passive impedances on a grid of constant r and x circles.
It contains the corresponding reflection coefficients in polar co-ordinates; the angle being read on the peripheral scale and the magnitude being calculated using:
The upper half of the diagram represents positive reactance values (inductive elements).
The lower half of the diagram represents negative reactance values (capacitive elements).
Impedance or Admittance values read from the chart are normalized values.
Moving away from the load (i.e. toward the generator) corresponds to moving in a clockwise direction.
A complete revolution around the chart is made moving a distance L = λ/2 along the transmission line.
The same chart can be used for reading admittance.
The center of the chart corresponds to the impedance-matched condition since Γ = 0.
A circle centered at the origin is a constant Γ circle.
Moving along the lossless transmission line is equivalent to moving along Γ circle.
For impedance Z reading, the point (Γr = 1 and Γi = 0) corresponds to an open circuit.
For admittance Y reading, the same point corresponds to a short circuit.
The impedance distance λ/4 from ZL is equal to YL.
The SWR can be found by reading R at the intersection of the constant Γ circle with real axis.
The Smith Chart can be used to find: ΓL from ZL and vice-versa, Zin from ZL and vice-versa, Z from Y and vice-versa, the SWR, and the impedance matching.
The horizontal radius to the left of the centre corresponds to voltage minimum and current maximum (
Vmin, Imax).The horizontal radius to the right of the centre corresponds to the standing wave ratio (SWR), the voltage maximum and the current minimum (Vmax, Imin).
References:
1. RF Circuit Design - C. Bowick2. RF and Microwave Wireless Systems - K. Chang
3. Microwave Communications Engineering - Glover, Pennock, Shepherd
4. RF Design Magazine, 1988-2000
5. Microwave Journal, 1998-2000
6. Applied Microwave Magazine, 1995-2000
7. ARRL Handbook, 1990-20008. Ham Radio Magazine, 1970 - 1980