O dB , (decibel) e outras unidades logarítmicas:
dBA, Neper, dBr, dBc, dBm, dBW, dBk, dBm0, dBu, dBsr, VU, dBV, dBµ, dBµV/m, dBp, dBi, dBd, S unit, dBFS
Por PY4ZBZ (em 18-01-2006, atualizado 19-02-2020)
Obs. : dB : d minúsculo pois é a abreviação do prefixo deci e B maiúsculo pois é o símbolo da unidade bel (homenagem a Alexander Graham Bell)
O dB é uma unidade logarítmica muito usada em telecomunicações, por pelo menos dois motivos :
- O ouvido humano tem resposta logarítmica (sensação auditiva versus potência acústica)
- Em telecomunicações, se usam números extremamente
grandes ou pequenos. O uso de logaritmos torna estes números pequenos
e fáceis de manipular, e transforma produtos em somas e divisões
em subtrações.
O dB é um número relativo e permite representar relações
entre duas grandezas de mesmo tipo, como relações de potências,
tensões, correntes ou qualquer outra relação adimensional.
Portanto, permite definir ganhos e atenuações, relação
sinal/ruído, dinâmica, etc...
Por definição, uma quantidade Q em dB é igual a 10 vezes o logaritmo decimal da relação de duas potências, ou seja :
Q(dB) = 10 log ( P1 / P2 ).
Como a potência é proporcional ao quadrado da tensão dividida pela resistência do circuito, temos, aplicando as propriedades dos logaritmos (o log. do quadrado de n é duas vezes o log. de n) :
Q (dB) = 20 log ( V1 / V2 ) + 10 log ( R2 / R1)
ou ainda, na mesma resistência : Q(dB) = 20 log ( V1 / V2
)
Para ganhos por ex., P2 é a potência de entrada e P1 a
potência de saída do circuito.
Para atenuações, P1 é a potência de entrada
e P2 a potência de saída.
Atenuação é o inverso do ganho (em unidades lineares)
e é igual ao ganho em dB com sinal trocado.
A tabela seguinte fornece alguns valores típicos :
|
Q (dB) |
P1 / P2 |
V1 / V2 |
|
120 |
1 000 000 000 000 |
1 000 000 |
|
90 |
1 000 000 000 |
31 600 |
|
60 |
1 000 000 |
1 000 |
|
30 |
1 000 |
31,6 |
|
20 |
100 |
10 |
|
10 |
10 |
3,16 |
|
6 |
4 |
2 |
|
3 |
2 |
1,414 |
|
0 |
1 |
1 |
|
-3 |
0,5 |
0,707 |
|
-6 |
0,25 |
0,5 |
|
-10 |
0,1 |
0,316 |
|
-20 |
0,01 |
0,1 |
|
-30 |
0,001 |
0,0316 |
|
-60 |
0,000 001 |
0,001 |
|
-120 |
0,000 000 000 001 |
0,000 001 |
Observe que 0 dB (zero dB) equivale a uma relação
de 1, e 3 dB equivale a uma relação de 2 ( em potência), e 10 dB por acaso equivale a uma relação de 10.
Resumindo :
+3 dB equivale a multiplicar por 2
+10 dB equivale a multiplicar por 10
-3 dB equivale a dividir por 2
-10 dB equivale a dividir por 10
É fácil converter qualquer valor inteiro de dB na relação
correspondente, usando apenas 3 e 10 dB.
Por exemplo, 17 db:
17 = 10 + 10 - 3 dB ou em unidades lineares 10 x 10 / 2 = 50.
Portanto 17 dB equivale a uma relação de 50.
Exemplo de operações com com dB e as respectivas unidades lineares :
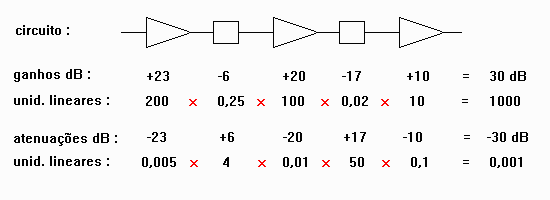
Outras unidades logarítmicas :
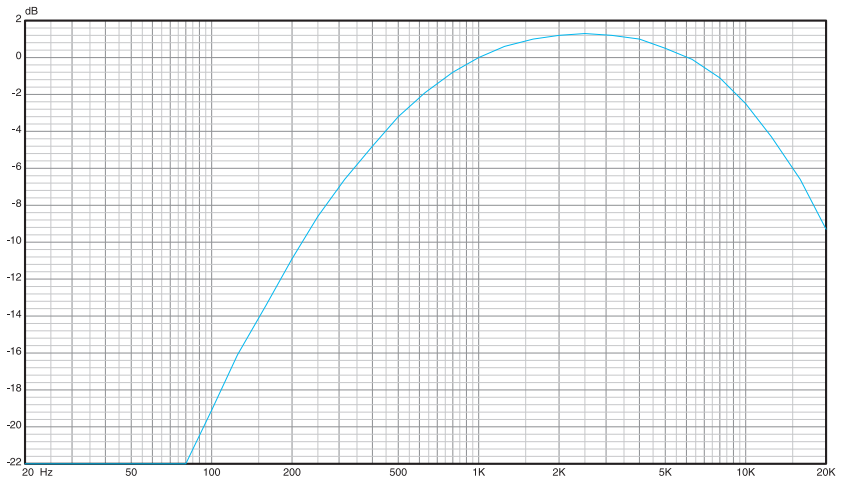
- O dBA : zero dBA equivale a uma intensidade sonora (pressão sonora) de 20 microPascal, e equivale aproximadamente ao limiar de audição. O limiar de dor se situa em torno de 120 dBA, ou seja, uma pressão 1 000 000 de vezes maior ou uma potência sonora 1 000 000 000 000 de vezes maior ! (a potência sonora é proporcional ao quadrado da pressão). O A se refere a um tipo de filtro de ponderação (weighting), que leva em conta a não linearidade do ouvido em freqüência. A figura seguinte mostra a curva de ponderação A. A intensidade sonora também pode ser medida sem essa ponderação, em dB ou dBZ, em relação à referencia de 20 microPascal = 0 dB. Por exemplo, um som com freqüência de 100 Hz e intensidade de 60 dBA tem uma intensidade não ponderada de 79 dB, pois a curva A apresenta 19 dB de atenuação em 100 Hz. Em 1000 Hz (e 6000 Hz), as medidas em dB e dBA são idênticas.
- O Neper : Uma unidade bastante usada em calculo é o Neper, que é igual ao logaritmo neperiano da razão de duas tensões (ou correntes) na mesma impedância. Obs.: 1 N = 8,65 dB.
- O dBr é uma unidade relativa de medida de nível,
em relação ao ponto zero de transmissão, (0 TLP),
onde geralmente o nível do tom de teste é de 0 dBm.
Apenas indica o somatório dos ganhos e atenuações
num ponto qualquer em relação ao ponto de referencia, ou
ponto zero de transmissão.
O dBc é uma unidade de medida de sinais em relação à portadora (carrier), como por exemplo espúrios ou ruídos laterais.
- O dBm é uma unidade de medida de potência : 0 dBm = 1 mW (Não importa em qual resistência !)
P (dBm) = 10 log P (mW)
Portanto : 3 dBm = 2 mW , 30 dBm = 1W , -30 dBm = 1 microW
e ainda:
- O dBW é uma unidade de medida de potência: 0 dBW = 1W = 30 dBm
- O dBk é uma unidade de medida de potência: 0 dBk = 1 kW = 30 dBW = 60 dBm
- O dBm0 é uma unidade de medida de potência relativa
ao ponto zero.
Geralmente, é usado para indicar o nível de outros sinais,
como pilotos, tons de sinalização, ruído, fuga de
portadora, diafonia, etc., em relação ao tom de teste.
Ex.: um tom de sinalização de –20dBm0 terá uma
potência (ou nível) de –28 dBm num ponto onde o tom de teste
tem –8dBm. ( ponto de –8dBr).
Ex.: se num determinado ponto o nível do ruído é
de –34 dBm e o nível do tom de teste é de –4dBm, então
o nível do ruído é de –30dBm0.
Obs.: a relação sinal/ruído em db é o nível
do ruído em dBm0 com sinal trocado.
Relação entre dBm, dBr e dbm0 : dBm
= dBr + dBm0
- O dBu é uma unidade de medida de tensão, onde 0 dBu = 0,775V.
Um voltímetro pode ter uma escala graduada em dBu, relacionada com a tensão V por:
U(dbu) = 20 log ( V / 0, 775 )
Como 0,775V corresponde a tensão desenvolvida por 1 mW num resistor
de 600 ohms, a leitura em dBu corresponde a potência em dBm, desde
que seja efetuada em um circuito cuja resistência de terminação
é de 600 ohms.
Em qualquer outra impedância Z (resistiva), deve ser somado à
leitura em dbu um fator de correção:
F(db) = 10 log ( 600 / Z ) para obter o valor da potência em dBm:
P (dBm) = U (dBu) + F (dB).
Alguns valores de F e Z : 6 dB em 150 ohms, 9 dB em 75 ohms, 10,8 db em 50 ohms.
- O dBsr (scale reading) ou seja, dB lidos na escala (do voltímetro). É o mesmo que o dBu.
- O VU : unidade de medida de tensão, usada em estúdios de radio : 0 (zero) VU = +4 dBm = 1,228 V em 600 ohms.
O dBV é uma unidade de medida de tensão em relação à 1 Volt : 0 dBV = 1 V
- O dBµ : (ou dBµV) unidade de medida de tensão onde 0 (zero) dbµ = 1 microvolt, usada para medir tensões muito pequenas como por ex. sensibilidade de receptores. Zero dbµ em 50 ohms equivale a uma potência de -107 dBm.
- O dBµV/m : unidade de medida de intensidade de campo elétrico E, onde 0 (zero) dbµV/m = 1 microvolt/metro.
Conversão de dbµV/m em dbµV, em função do ganho isotrópico Gi da antena e da frequência F, em 50 ohms:
V( dbµV) = E( dbµV/m) + Gi - 20logF(MHz) + 29,8
- O dBp : dB ponderado psofometricamente (psofos= ruído), ou seja, que leva em conta o somatório das respostas em frequência do ouvido e da cápsula receptora telefônica, e usado para medir ruído e relações sinal/ruído em telefonia. Aplica-se também ao dBm > dBmp e dBm0 > dBm0p.
- O dBi : usado para expressar o ganho de uma antena em relação a antena ISOTRÓPICA. A antena isotrópica tem um diagrama de irradiação esférico, ou seja , irradia igualmente em todas as direções. O dBi é muito usado em cálculos de enlaces de telecomunicações, pois a atenuação de propagação é sempre calculada entre antenas isotrópicas. A antena isotrópica é uma referencia teórica, sendo de difícil construção prática.
- O dBd : usado para expressar o ganho de uma antena em relação ao DIPOLO de meia onda. O dipolo de meia onda é a antena ressonante mais simples e fácil de ser construída e por isso é muito usada como referencia. Em espaço livre, o ganho do dipolo de meia onda é de 0 dBd = 2,15 dBi
- O ponto S : unidade usada por radio amadores, o ponto
S de signal-Strength, intensidade de sinal, teoricamente equivale a 6 dB, ou seja, duas vezes mais tensão no conector de antena do
receptor. Teoricamente também, S 9 equivale a 50 microvolts (-73 dBm em 50 ohms)
abaixo de 30 MHz, e 5 microvolts (-93 dBm) acima de 30 MHz. Mas na pratica, apenas
alguns raros medidores de unidades S são calibrados para S9, e mesmo
assim o resto
da escala sendo muito impreciso, principalmente acima de 30 MHz !. Para
valores acima de S 9 , usa-se o
dB, por exemplo: S9+20 dB. Conversões dBm/volts/unidades S aqui.
- O dBFS : usado para expressar níveis de amplitude em sistemas digitais. O nível máximo que ainda não sofre ceifamento (clipping) é definido como 0 dBFS (zero dBFS) (FS=Full Scale). Por exemplo, se a tensão de entrada de uma placa de som está com a metade do nível máximo de quantização do conversor A/D, ela está com -6 dBFS. Para ter certeza que algumas amostras realmente se situam no pico da onda, é escolhida uma freqüência de teste de 997 Hz, que não é submúltiplo exato das taxas de amostragem padronizadas.
Soma de sinais não coerentes (ruído branco ou sinais de freqüências diferentes) :
Por exemplo, qual é a potência total de um sinal com 10
dBm somado a um ruído de 6 dBm ?
Solução : a diferença entre as parcelas é
10 dBm - 6 dBm = 4 dB (obs. : subtrair potências em unidades logarítmicas
equivale a fazer um quociente em unidades lineares, portanto, o resultado
é um numero adimensional, o dB). No gráfico da figura seguinte,
obtemos para uma diferença de 4 dB o valor de 1,45 dB. A soma dos
dois sinais tem uma potência de 10 dBm + 1,45 dB = 11,45 dBm.
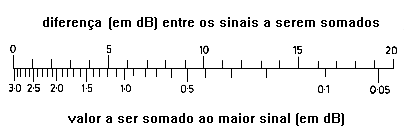
Sinais não coerentes se somam em potencia. Sinais coerentes (mesma freqüência) se somam (vetorialmente) em tensão. É preciso calcular esta soma vetorial de tensão e depois passar para potencia. No caso de 2 sinais não coerentes, temos:
P1 = potencia maior, P2 = potencia menor,
diferença em dB : dP(dB) = P1(dBm)-P2(dBm) = 10log(P1/P2) : escala superior do gráfico acima.
valor a ser somado (em dB) à maior potência (em dBm):
10log[(P1+P2)/P1] = 10log[1+(P2/P1)] ; como P2/P1=antilog(-dP/10), temos:
10log(1+antilog(-dP/10)): escala inferior do gráfico acima.
Somar x dB a uma potencia em dBm equivale a multiplicar esta potencia em unidades lineares (W, por exemplo) por um numero adimensional igual ao antilog(x/10), portanto resulta em uma nova potencia, e que pode ser expressa por exemplo em dBm. Portanto, a soma de dBm com dB resulta em dBm !. Da mesma forma, subtrair dB de uma potencia em dBm equivale a dividir esta potencia por um numero adimensional, resultando em uma nova potencia. Portanto, subtrair dB de dBm resulta em dBm !.
Obs.: Somar diretamente os valores em dBm não faz sentido, pois equivale a multiplicar estas potencias em unidades lineares! Por exemplo, as seguintes somas de sinais não coerentes:
0 dBm + 0 dBm = 3 dBm (e não 0 dBm ! )
0 dBm + 3 dBm = 4,76 dBm (e não 3 dBm !)
-2 dBm + 2 dBm = 3,45 dBm (e não 0 dBm !)
O sinal + nesse caso se refere às unidades lineares de potencia, ou seja, indica que estamos somando as potencias em unidades lineares (W, mW, etc...) correspondentes aos valores em dBm.
Mas, somar dB a dBm equivale a multiplicar a potencia (em dBm) por um numero adimensional (dB), o que resulta em uma nova potencia (dBm):
0 dBm + 0 db = 0 dBm
0 dBm + 3 dB = 3 dBm
-2 dBm + 2 dB = 0 dBm
Ou ainda, subtrair valores em dBm resulta em um valor em dB (e não dBm). Pois subtrair unidades logarítmicas equivale a uma divisão em unidades lineares ! Subtrair valores em dBm equivale portanto a um quociente de duas potencias, e esse quociente ou relação é adimensional, portanto equivale a um valor em dB ! Por exemplo:
13 dBm - 10 dBm = 3 dB (e não 3 dBm)
pois 13 dbm = 20 mW e 10 dBm = 10 mW. E o sinal - equivale a uma divisão
ou seja 13 dBm - 10 dBm equivale a 20 mW / 10 mW = 2 (e não 2 mW). E 2 equivale a 3 dB.
73 de Roland.