FUNDAMENTALS OF
ELECTROMAGNETIC RADIATION
2.3
RADIATION FROM A SHORT CURRENT FILAMENT
Figure
2.5 shows a short, thin filament of current located at the origin and oriented
along the z axis. For this source the vector potential has only a z component
and is a solution of Eq. (2.19), that is,�
where
Jz = I/dS and
dS is
the cross sectional area of the current filament of length dl. The
volume dV
= dS dl occupied by the current is of
infinitesimal size so the source term can be considered as located at a point.
There is spherical symmetry in the source distribution, so
�will be a function
only of the radial distance r away from the source.
�will not be a
function of the polar angle
�or the azimuth angle
�shown in Fig.
2.5.
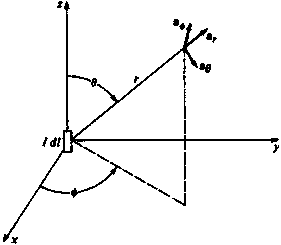
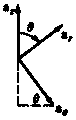
Figure
2.5 The short current filament and the spherical coordinate
system.
For values of r not� equal to zero,
satisfies the equation
as
obtained by expressing the Laplace operator
in spherical coordinates and dropping the derivatives with
respect to
�and
, then
, and the equation
obtained from Eq. (2.20) for
becomes�
This
is a simple harmonic‑motion equation with solutions
�and
, where
and
, are constants. If we choose the first solution and restore
the time factor we obtain
Now
ko = w/c, where
�is the speed of light
in free space, so
This
is a wave solution corresponding to an outward propagating wave, since the
phase is retarded by the factor
kor
and
the corresponding time delay is r/c. The other solution with the constant C2
corresponds to an inward propagating spherical
wave and is not present as part of the solution for radiation from a current
element located at r = 0. Our solution for A. is now seen to be of the form
In order to relate the constant
�to
the source strength, we integrate both sides of Eq. (2.19) over a small
spherical volume of radius
�We note that 
, so upon using the divergence
theorem we obtain��
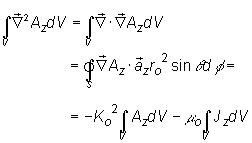
Now
�and
�varies as 1/r;
consequently, it we choose
�vanishingly small the
volume integral of
, which is proportional
to
�vanishes. The volume
integral of
�gives
Jz dS dl = I dl. which
is the total source strength. Also
so
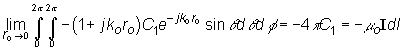
Our
final solution for the vector potential is��
The
vector potential is an outward propagating spherical wave with an amplitude
that decreases inversely with distance. The surfaces of constant phase or
constant time delay are spheres of fixed radius r centred on the
source. The phase velocity of the wave is the speed of light c, or
. The distance that corresponds to a phase change
�is the wavelength
�and
may be found from the relationship
; thus
From our solution for the vector potential we
can readily find the electromagnetic field by using Eqs. (2.13) and (2.18).
This evaluation is best clone in spherical coordinates, so we first express
�in
terms of components in spherical coordinates by noting that (see Fig.2.5)
and
consequently���
We
now use Eq. (2.13) to obtain
and
use Eq. (2.18) to obtain
�
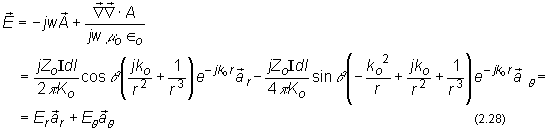
When
r is large relative to the
wavelength
, the only important terms are those that vary as 1/r.
These terms make up the far zone, or radiation field, and are
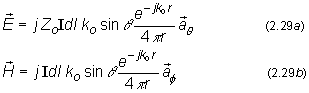
We
note that in the far zone the radiation field has transverse components only;
that is, both
�and
�are perpendicular to
the radius vector as well as perpendicular to each other. The ratio of
�to
�equals the intrinsic
impedance
�of free space. This
is a general feature of the radiation field from any antenna. In vector form,
one always finds that the radiation field in the far-zone region
satisfies the relations
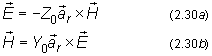
where
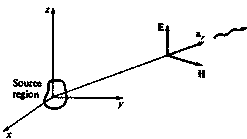
. This spatial relationship is illustrated in Fig. 2.6.
We
also note that both
�and
�vary as
. Thus the radiated field is not a spherically symmetric
outward-propagating wave as was found for the vector potential. This is
also a general feature of all radiation fields-the electromagnetic
radiation field can never have complete spherical symmetry.
�
Figure 2.6
Spatial relationship of the electric
and magnetic tip fields in
the radiation zone.
The
complex Poynting vector for the radiation field is
and
is pure real, and directcd radially outward. The radiated power per unit area
decreases as
, as expected because of the spreading out of the held as it
propagates radially outward. This is the inverse-square-law
attenuation behavior discussed in Chap.1.
Before we procced any further with the
discussion of the radiation field we
return
to an examination of the other terms in Eqs. (2.27) and (2.28). These
terms,
varying as
�and
, will become predominant when
�and
make
up
the near-zone reactive field. It is a reactive field because the near-zone
magnetic
and electric fields have a pure imaginary Poynting vector, indicating
reactive
power rather than real radiated power. If
�is verv small-
so that we
can
replace
�by unity-
then� the near-zone fields become
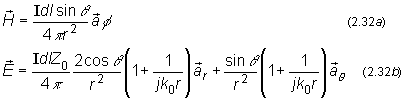
For
�we can also replace
�by
.
We also note
that the charge Q at the end of the current filament must change according to jwQ = I �since current is the rate of change of
charge. Hence
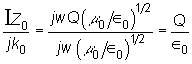
and
Eq. (2.32b) become
The
result, given by Eqs. (2.32a) and (2.32c) can
be recognized as
the static
Although
the near-zone fields do not contribute to the radiated power, they do
represent a storage of electric and magnetic energy in the space immediately
surrounding the antenna and account for the reactive part of the impedance seen
looking into the antenna terminals. Thus, except for impedance calculations,
the near-zone fields are not of great interest.
We
could obtain the complete complex Poynting vector
�by using the complete
expressions for the fields. If this is done, it will be discovered that the
real part, the part that will give rise to radiated power, involves only the
radiation field and is given by our earlier expression [Eq. (2.31)].