(2.12)
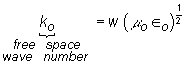
This is the
equation that must be solved to find the electric field directly in terms of
the specified current source
or,
i.e.,
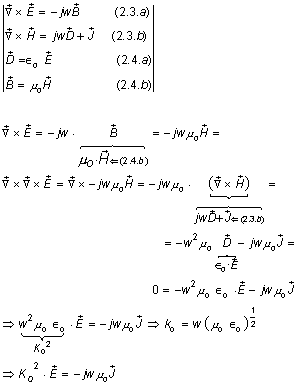
MAXWELL’S EQUATIONS AND BOUNDARY CONDITIONS FOR ANTENNAS:
2.2 VECTOR
AND SCALAR POTENCIALS:
|
This is the
equation that must be solved to find the electric field directly in terms of
the specified current source
i.e.,
|
|
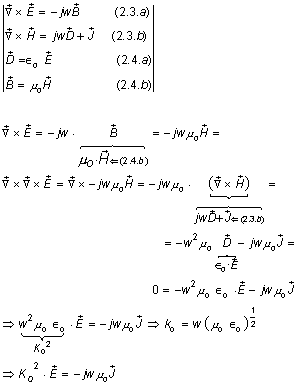In practice
a simpler equation to solve is obtained by introducing the vector potencial
and scalar potencial
.
(2.13)
because
is called vector
potencial.
(2.13) in
(2.3.a):
(2.3.a)
Any
function with zero curl can be expressed as the gradient of a scalar function.
(2.14)
(2.3.b)
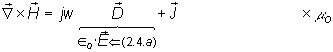
Using the expansion 
Besides
(2.14) assumption: 
(2.14)
it’s also
assumed that Eq.(2.3.b) will hold
|
|
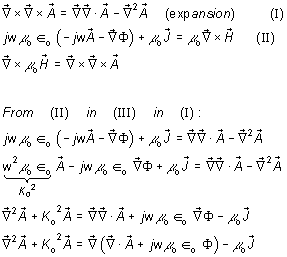
(2.13)
fixed.
So far only
the curl of
is fixed by the
relation (2.13). Thus, we are still free to specify the divergence of
. In order to simplify the equation for
we choose:
(2.15)
lorentz condition
Our
equation for
now becomes the
inhomogeneous Helmholtz equation:
(2.16)
Using
(2.14) and (2.15) in Eq. (2.3.c)
(2.3.c)
(Gauss’ Law)
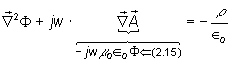
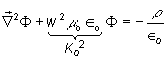
However, the change is not an independent
source term for time-vary ing fields, since it’s is related to the current by
the continuity equation (2.3.e).
(2.3.e)
, and it is not
necessary to solve for the scalar potential
.
Using (2.15) (Lorentz condition) in (2.14)
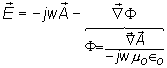
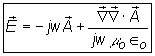(2.18)
R.E.COLLIN-ANTENNAS-p.19
The simplification obtained by
introducing the vector potencial
may be appreciated by
considering the case of a z-directed current
source
in which case
and
is a solution of the
scalar equation
The equation satisfied by the electric field is a vector equation even when the current has only a single component.