Fourier transform

For testing a Fourier transform I need a more complex signal than an ordinary sinus. I want a mix of three frequenties f, 2f and 5f with an arbitrary phase. In order to keep Engine() simple I added a class Signal:

public class Signal
{
    /** A class to represent an input-signal for the FFT
    *   the input-signal consists of 3 sinus-signals:
    *   a1*sin(2*pi*f*t) + a2*sin(2*pi*2*f*t+phi2)+a5*cos(2*pi*5*f*t)
    */
    
    private double a1;
    private double a2;
    private double a5;
    private double f;
    private double phi2;
    
    public Signal(double f, double a1, double a2, double a5, double phi2)
    {
        this.f = f;
        this.a1 = a1;
        this.a2 = a2;
        this.a5 = a5;
        this.phi2 = phi2;
    }
    
    public double getSample(double t)
    {
        double pi2 = Math.PI * 2;
        return  a1 * Math.cos(pi2 * f * t)
                + a2 * Math.sin(pi2 * 2 * f * t + phi2)
                + a5 * Math.sin (pi2 * 5 * f * t);  
    }
}

Signal is used in Engine():


package testFFT;

import util.ShowPlot2d;
import util.Signal;

public class Engine {
  // a more complicated testsignal

  public Engine() {

  }

  public void plotSignal() {

    double f = 1.0E3;
    double a1 = 1.0;
    double a2 = 0.8;
    double a5 = 1.2;
    double phi = Math.PI / 4;
    int numP = 109;
    Signal mySignal = new Signal(f, a1, a2, a5, phi);

    // 3 periods with 36 points per period

    double[] plotData = new double[numP - 1];

    for (int i = 0; i < numP - 1; i++) {
      double degr = 10 * i;
      double perT = 1 / f;
      double t = (degr / 360) * perT;
      double y = mySignal.getSample(t);
      plotData[i] = y;
    }

    int numberOfPlots = 1;
    ShowPlot2d myPlot = new ShowPlot2d(numberOfPlots);
    double scaleFactor = 100;
    myPlot.add(plotData, scaleFactor, "a complicated sinewave");
    myPlot.showFigure();
  }
}

with the following output:

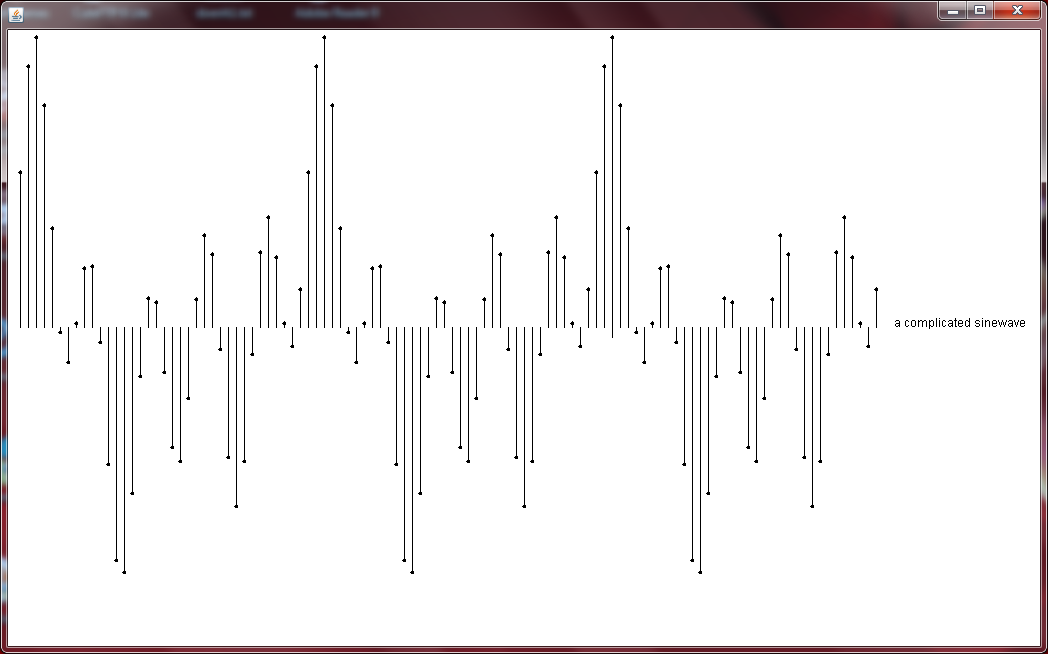
What is the sample frequency of the above signal? There are 36 points per period of the base frequency f. So the sample-frequency is 36* f.

The next piece of java-code is fillArray3. This method calculaties the DFT, the Discrete Fourier Transform. For that I needed a dft-program. Because I don't (yet) need real-time respons I simply coded the DFT-formulas directly in java without any attempt for efficiency. The dft-method:

private Complex[] dft(double[] x)
    {        
        int n = x.length;
        Complex[] xX = new Complex[n]; // FFT-bins
        for(int k = 0; k < n; k++)
        {
           Complex accum = new Complex(0.0, 0.0);
           for (int nn=0; nn < n; nn++)
           {
            Complex wnkN = Complex.expjphi(-2*Math.PI*nn*k/n);
            Complex prod = wnkN.multiply(x[nn]);
            accum = accum.add(prod);            
           }
           xX[k] = accum;
        }
        return xX;
    }

Which is called by the following snippet of code:

...
    for (int i = 0; i < numP - 1; i++) {
      double degr = 10 * i;
      double perT = 1 / f;
      double t = (degr / 360) * perT;
      double y = mySignal.getSample(t);
      plotData[i] = y;
    }
    double x[] = plotData;
    Fourier myFourier = new Fourier();
    Complex bins[] = myFourier.dft(x);
    for (int i = 0; i < bins.length; i++) {
      plotData1[i] = bins[i].getReal();
      plotData2[i] = bins[i].getImaginary();
      plotData3[i] = bins[i].magnitude();
    }

    int numberOfPlots = 3;
    ShowPlot2d myPlot = new ShowPlot2d(numberOfPlots, "Three plots");
    double scaleFactor = 1;
    myPlot.add(plotData1, scaleFactor, "real");
    scaleFactor = 1;
    myPlot.add(plotData2, scaleFactor, "imag");
    scaleFactor = 1;
    myPlot.add(plotData3, scaleFactor, "magnitude");
    myPlot.showFigure();
...

and the output is:

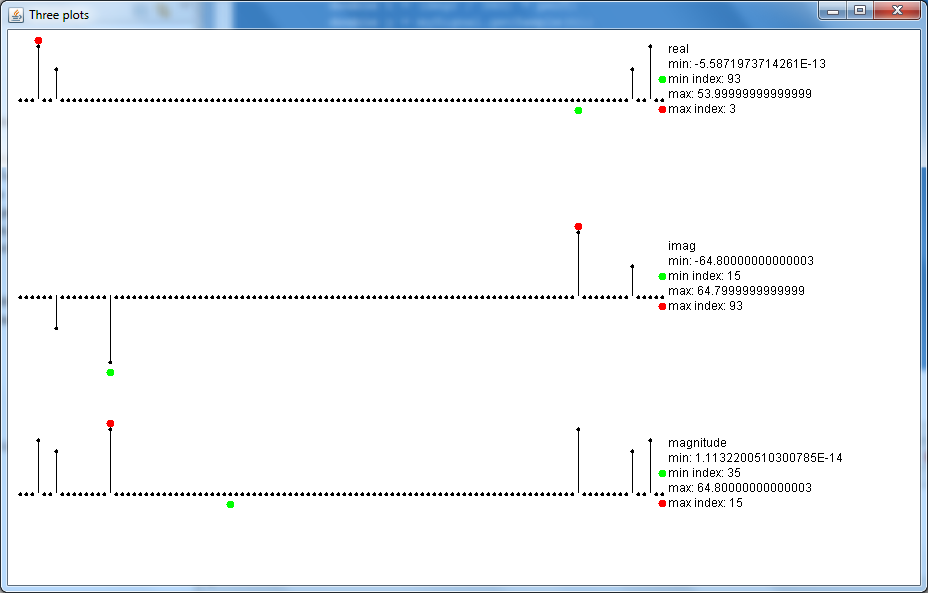
The results are numerically shown in the following table:

Discrete Fourier Transform

Bin-number	Magnitude	Real part	Imaginary part
3 (f)	54	54	0
6 (2f)	43.2	30.5	-30.5
15 (5f)	64.8	0	-64.8
93 (5f)	64.8	0	64.8
102 (2f)	43.2	30.5	30.5
105 (f)	54	54	0

The basic frequency f is in bin 3. There are 36 points per period of the base frequency f. So the sample-frequency is 36* f. There are 108 points, so every bin is fs/108= 36*f/108 = f/3. So bin 3 is f, bin 6 is 2f and bin 15 is 5f. Because the dft-transforms of f only have real parts, f must be a cosine. You can find that in the code for "Signal". The dft-transform for 5f is obviously a sine. The signal 2f is complex. There is a 45 degree angle between the real and imaginary part. This can also be found in the java-code for Signal. The amplitude for f is 54+54 = 108. Divided by the number of bins ==> 1. That is correct. The other amplitudes also are in correspondence with the code in Signal.

If you transform a signal into its Fourier components there is also a way back; the Inverse Discrete Fourier Transform. The code is almost the same as for the dft:

private Complex[] idft(Complex[] X)
    {        
        int n = X.length;
        Complex[] x = new Complex[n]; 
        for(int k=0; k < n; k++)
        {
           Complex accum = new Complex(0.0, 0.0);
           for(int nn=0; nn  < n; nn++)
           {
            Complex wnkN = Complex.expjphi(2*Math.PI*nn*k/n);
            Complex prod = wnkN.multiply(X[nn]);
            accum = accum.add(prod);            
           }
           x[k] = accum.multiply( (double) (1.0/n));
        }
        return x;
    }

By clearing bins 6, 15, 93 and 102 after the dft and before the idft an ideal lowpass-filter is the result: