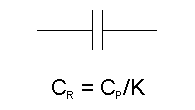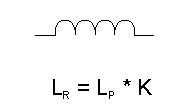A change in termination resistances requires that the impedances of each inductor and capacitor be changed by a factor equal to the change in resistance. So if each resistance termination is changed by a factor of K, then the capacitances must be divided by K and the inductors must be multiplied by K.

Since K is likely to be greater than one, making a capacitor smaller for any given frequency will increase the reactance so division is needed. Making the inductance larger for a given frequency will make the inductive reactance greater. Even if K were less than one, the argument still holds.

Since the prototypical resistance is 1 Ohm, then our factor, K, is merely the new input and output resistance. The input and output resistances are both 1 Ohm and the new input and output resistances must be equal. (Translations exist for unequal input and output resistances, but this application does not support them.)

Conceptually the reactances of the new components are made to match the new resistance. Decreasing the capacitance and increasing the inductance increases the reactance of each. Correspondingly, increasing the capacitance and decreasing the inductance decreases the reactance of each.

When doing multiple translations, make the resistance translations first. This is because some of the filters require inductors to translate to capacitors and conversely. Some filters require inductors to translate into a resonant circuit and it would be a difficult chore to determine the original prototypical component's nature.

To translate from the prototypical capacitance values, perform this mathematical manipulation:

To translate from the prototypical inductance values, perform this mathematical manipulation: