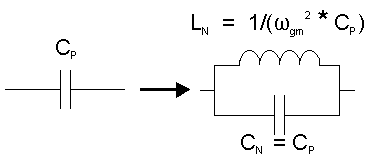
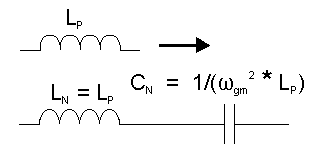A translation from a low pass prototype requires three steps. The first of which is to do a resistance translation (q.v.) and second to do a low pass frequency translation using this conversion factor.
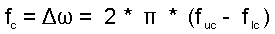
where fc, normally the corner frequency in a low pass or high pass filter, is replaced by the difference between the upper and lower corners, (f uc - f lc) times 2 * pi.
Having done those two translations, find the geometric mean of the two frequencies f uc and f lc by using
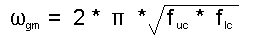
The geometric mean and the arithmetic mean are only a few percentage points different when pass bandwidths are small, but become larger as bandwidths increase.