There has been much discussion in the rec.radio.amateur.antenna (r.r.a.a.) newsgroup about whether or not modeling a short, loaded antenna using a lumped load model (inductor) is or is not a fair representation of the same antenna using a physical ("distributed") coil. There has been argument about what the current distribution is on the radiator and whether the current "into" and "out of" the loading coil is constant or not.

This discussion aroused my interest and I decided to do some unbiased investigation. This note is a report of my efforts to date and is not necessarily complete.

The Short Loaded Monopole.

Here is what a paper by Hansen¹ says that relates to the discussion at hand:

"In principle the loading inductor functions by keeping the current distribution nearly (emphasis added) constant from the feed to the load point, thereby increasing the current moment. Since the transmitting parameter, radiation resistance, varies as current moment squared, and since the receiving parameter, effective length, varies with the current moment, it is clear that inductive loading will improve short monopole performance. There is a value of loading reactance which allows the current to approximate a constant value out to g·h (the fractional distance of the coil position from the feed) with a linear drop-off beyond. This value of inductance is, however, insufficient to produce input impedance resonance. The resonant value of load produces a modest current peak (emphasis added) just beyond g·h so that the current moment is increased by an additional amount over that expected from the constant current model."

It is not the intention of this note to prove or disprove Hansen's work but simply to point out that the quoted paragraph conflicts with most of the popular ham thinking and oft cited references such as Devoldere's Low-Band DXing ² and Brown's paper on mobile antennas ³ which fail to show this peaking in short (< 0.1 lambda) loaded antennas. In fairness to Devoldere, it should be pointed out that he never shows antennas shortened by much beyond 50%. One other place where this current peaking has been reported is in the work of Cebik.

To see if I could duplicate the Hansen and Cebik findings and to investigate the legitimacy of using the NEC load model I developed a model of a short vertical that used one of two inductive loads: 1) a coil model that is comprised of "wires", or 2) a length of wire the same height as the coil, with a lumped RLC load at the midpoint.

The models were "built" using MultiNEC invoking EZNEC 3.0 or double-precision NEC-2 as the calculating engines. The following graphics were all generated with MultiNEC.

To stay within the limitations of NEC with respect to segment lengths, wire spacing, and so forth, the frequency was set to 7.150 MHz, the radiator total height was set to 120 inches (0.07 lambda). The part of the radiator below the loading inductance was comprised of two wires, one of one segment with the source at the midpoint and the other of variable segment length, adjusted to maintain nearly constant segment lengths throughout the model. The radiator above the loading inductance was similarly segmented. All wires are 12 AWG copper.

Perfect ground was used so that a direct ground connection could be used. To see the effects of ground loss a load can be put in the bottom wire.

Model descriptions.

Case 1 is shown for completeness and is a monopole with no loading of either type. The model has four wires; 1) a one-segment wire that includes the source, 2) a multiple segment wire located between the source wire and any loading, 3) an eight-inch long, three-segment wire centered on the length of the monopole (i.e. 60 inches above the feed point) and 4) the multiple segment wire that makes up the balance of the radiator. Segment lengths were adjusted to make each segment the same, or nearly the same, length.

Case 2 uses a model that also has four wires; 1) a one-segment wire that includes the source, 2) a multiple segment wire located between the source wire and the load wire, 3) an eight-inch long, three-segment wire centered on the length of the monopole where a "lumped" RLC ("Type 0") is load placed at its center and 4) the multiple segment wire that makes up the balance of the radiator above the load. Segment lengths were adjusted to make each segment the same, or nearly the same, length. The monopole is brought to resonance by using the resonating function of MultiNEC to adjust the inductance of the load. The Q of the load can be, and was, set by adjusting the "R". More on this later.

Case 3 uses a model similar to the other two cases, except the three-segment load wire is replaced by a wire coil ("distributed load") consisting of sixteen turns of 12 AWG wire, spaced 0.5 inch between adjacent turns, for a total height (length) of eight inches. The coil is centered on the length of the monopole and the monopole is brought to resonance by using the resonating function of MultiNEC to adjust the radius of the coil. Eight, single segment wires arranged in octagonal form approximate each turn of the circular coil, for a total of 128 single-segment wires.

Radiator current distribution plots.

The following figures are plots of the current distribution on the wires making up each of the models. At first glance, some of the plots may be disconcerting, so a few words of explanation are in order. It is important to remember when viewing the plots that, unless otherwise specified, the horizontal, x-axis of all of the plots, shows the segment numbers of the wires making up the model and does not represent the physical length (height) of the antenna.

Figure 1 shows the Case 1 unloaded monopole current distribution by segment number. In this particular case, the distance along the x-axis does closely correspond to the length of the radiator and the nearly linear decay of the current from the 1 Amp source to the open end of the antenna is exactly what is as expected for this electrically short radiator.

Figure 1.

Figure 2 shows the Case 2 monopole current distribution by segment number. In this particular case, the distance along the x-axis also closely corresponds to the length of the radiator.

Figure 2.

Figure 3 shows the Case 3 monopole current distribution by segment number. In this case, the x-axis does not represent length along the antenna. The coil consists of 128 wires (and segments) but they occupy only 8 inches of the total length (height) of the radiator.

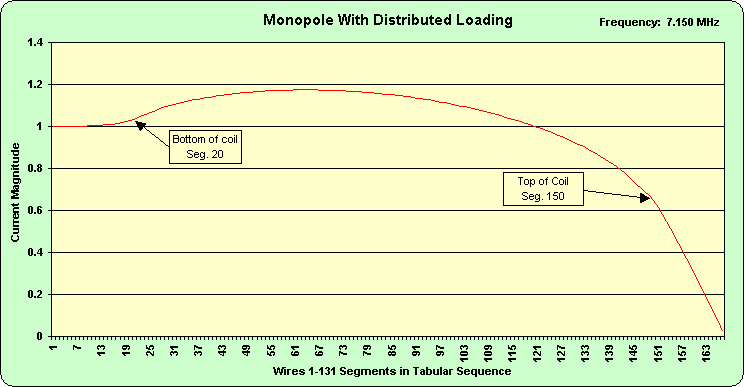
Figure 3.

Figure 2 and Figure 3 clearly show the peaking of the current that Hansen and Cebik write about. The following figures are plots of the current distribution on the wires below (Figure 4) and above (Figure 5) the load. Figure 4 shows the current peaking in greater detail. Figure 5 shows the expected nearly linear decrease in current from the load toward the open end.

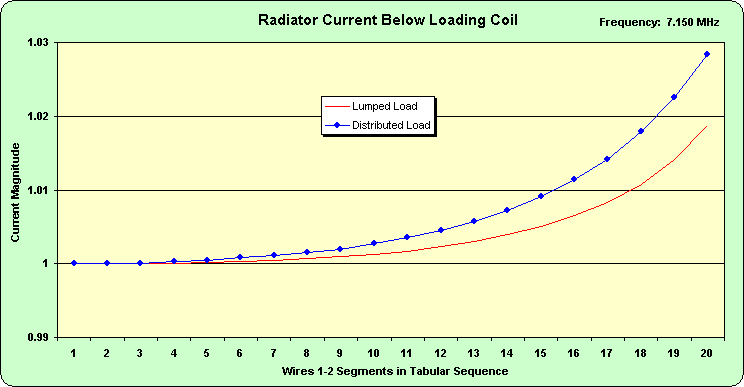
Figure 4.

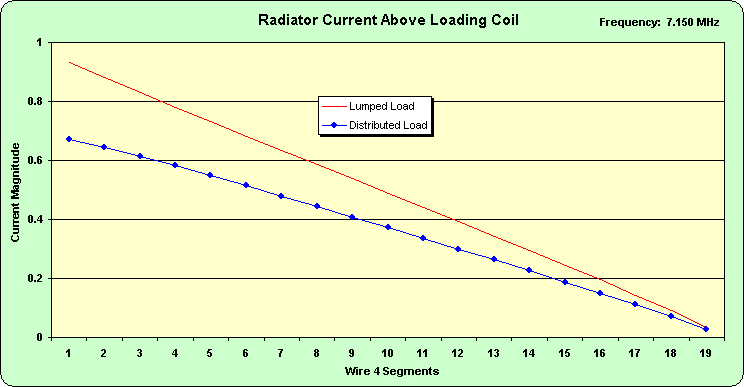
Figure 5.

The main difference between Cases 2 and 3 is the respective magnitudes of the currents. In Case 2, the current is lower in the bottom section and higher in the upper section than it is in Case 3. In both cases, however, the trends are similar and it isn't clear to me that they are significantly different. They certainly don't have much of an impact on the efficiency of the antenna.

Although it is commonly thought that the current distribution along the radiator has a direct impact on the efficiency of the antenna this isn't the case. Referring again to Hanson: "radiation resistance, varies as current moment squared". It is the change in the radiation resistance that impacts the efficiency, hence the gain, of the radiator in the real world situation. Absent conductor and ground losses, the unloaded, non-resonant monopole has the same efficiency as a resonant structure of the same size. The current distribution and its effect on radiation resistance make a difference only when loss is introduced.

Comparison of Currents on Loading Structures.

Figure 6 shows the segment currents in the three-segment wire that contains the lumped RLC load. The calculated current is shown in red. While it is somewhat of a stretch to use just three data points to derive a trend, the blue trace is a polynomial fit to the data. Comparing the curve fit data in Figure 6 to Figure 7 below we have almost exactly the same pattern. There is a peak in the current at about 30% of the height of the section of the radiator that comprises the loading structure and it doesn't seem to matter whether the loading is from a distributed coil or a lumped mathematical load.

Figure 6.

Figure 7 shows the segment currents in the 128 segments comprising the wire coil. The continuation of the current peaking is easily observed.

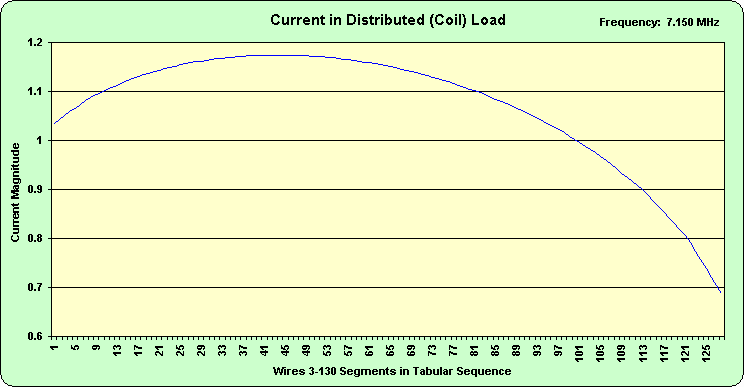
Figure 7.

If we could make the lumped load section 128 segments long with 128 small loads without violating the segment length rules then I believe that the relative current distribution in each segment would very similar to that in the distributed coil. I don't believe that the individual segment currents would be the same because in the distributed load (coil) case the segments lie in planes different from the axis of the radiator. It appears to me that in any case what is observed is the current distribution along the length, in this case 8 inches, of the loading structure. The controversy in the r.r.a.a. discussion was whether the current in a loading inductance was constant throughout the coil. Clearly, if the coil has some length, it is a part of the radiating structure and is both "inductor" and "radiator."

Likewise, because of the limitations of NEC, a lumped load must be placed on a wire segment that must have some finite length, so it too is both inductance and radiator. If a modeled load could have zero length and it could be placed on a zero length segment, then I believe that the current "into" and "out of" the load would be identical. How could it be otherwise?

Comparing other parameters.

To return to the question of whether the lumped load model is a reasonable thing to use to model a radiator loaded with a distributed coil, I think it is necessary to look at parameters other than the current distribution. Modifying the current distribution is after all just a means to a desired end; an increase of the radiation resistance to improve the efficiency. As stated above, for the same length radiator if there were no losses to contend with, the non-resonant radiator is just as efficient and has the same gain and pattern as the resonant radiator. In fact, as Table 1 shows, each of the three models has a gain of 4.8 +/- dBi when the wire, load and ground losses are set to zero. A full height monopole would have a gain of 5.17 dBi under the same conditions.

Test Condition	Frequency (MHz)	Feedpoint R	Feedpoint X	Gain (dBi)
Monopole (no loading)	7.15	2.12	-j 859.8	4.80
Distributed Coil loading	7.15	4.15	+j 0.0	4.85
Lumped load (Q = inf.)	7.15	4.82	-j 0.23	4.81

Table 1 Perfect Ground, Zero Loss.

Thus to make meaningful comparisons, loss must be introduced. Changing the wire loss to copper is a first step. Table 2 shows the results of this change.

Test Condition	Frequency (MHz)	Feedpoint R	Feedpoint X	Gain (dBi)
Monopole (no loading)	7.15	2.23	-j 859.7	4.58
Distributed Coil loading	7.15	5.37	+j 0.0	3.72
Lumped load (Q = inf.)	7.15	5.05	+j 0.0	4.61

Table 2. Perfect Ground, Copper Loss.

Clearly the extra wire (and loss) in the distributed coil affects both the feed point resistance and the gain to a greater extent that the additional loss affects to other two models. But the comparison of the distributed and lumped loading is now unfair. Loss was introduced to the distributed coil while the lumped load remained unchanged. To correct this disparity the Q of the lumped load was adjusted. Table 3 displays the results for some other values of Q.

Test Condition	Frequency (MHz)	Feedpoint R	Feedpoint X	Gain (dBi)
Lumped load (Q = inf.)	7.15	5.05	+j 0.0	4.61
Lumped Load (Q=5400)	7.15	5.37	+j 0.0	4.34
Lumped Load (Q=1530)	7.15	6.19	+j 0.0	3.72

Table 3. Perfect Ground, Copper Loss, Variable Q.

These results are surprising to say the least. In the lumped load case, it requires a reactance of + j1647.5 to resonate the structure. Setting the load to 1.07 + j1647.5 (Q = 1530) makes the gain of the two cases equal. On the other hand, to get the feed point resistance to equal that of the distributed load model requires setting the lumped load Q to 5400. I suspect that the differences in current distribution make a simultaneous fit to both resistance and gain impossible. But both of these values are extraordinarily high. Which of these is a more representative comparison is questionable, although the differences in meaningful results are negligible.

As a sanity check, the r-f resistance of the wire in the coil (including proximity effects) was calculated as approximately 1.07 ohm. (To resonate the structure, the coil radius is 3.725638 inches. Thus there are 128 straight segments each 2.86 inches long for a total of 366 inches of 12 AWG copper.) So from this standpoint, the lumped load model with Q = 1530 is right on. All of this suggests that the Q of the distributed coil is greater than 1500 and maybe much higher.

This raises a question of whether it is possible to have a coil with a Q this high. Conventional wisdom and literature say not. Some loss as manifested by lower Q, is attributed to winding capacitance. At least one author doesn't believe that the classic approximations for inductance and winding capacitance are correct. See: Filters and an Oscillator Using a New Solenoid Model. But in this case, the only detrimental loss mechanism is the resistance of the wire. There isn't any dielectric, and loss due to radiation cannot be separately accounted for. In this regard, it appears to me that the lumped load scenario using a reasonable value for inductor Q is actually more "real world" than the distributed coil model and the critics who say otherwise are wrong.

Add to this the fact that the distributed coil model is very contrived to fit the limitations of NEC, and while in this case it could be built, other more realistic physical coils cannot be modeled without violating NEC guidelines.

Before leaving this, it is worth looking at the situation when there is much more loss in the system. Of course with a vertical antenna this loss usually comes from our old enemy, ground loss. While a NEC-4 analysis would be preferred, I don't yet have a license for it so I'll stick with the expedient method of using perfect ground and putting a resistive load in the bottom segment. It cannot be overemphasized that models using this technique are useful for comparison purposes but should not be thought of as representing any real world performance.

The following figures show the effects of ground resistance on the gain and feed point resistance for the copper wire monopole over an otherwise perfect ground.

Figure 8 shows the aforementioned coincidence of the gain values for the distributed load model and the lumped load model when the Q of the latter is set to 1530 and the ground loss is zero.

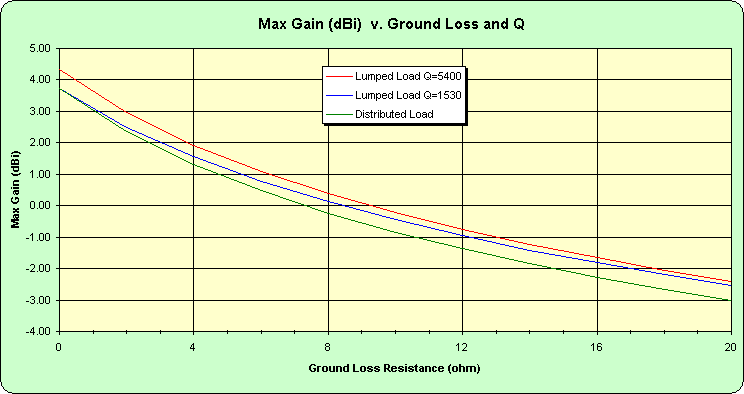
Figure 8.

Figure 9 shows the coincidence between the feedpoint resistance of the distributed load model and the lumped load model when the Q of the latter is set to 5400. The figure also shows the unsurprising linear increase of feedpoint resistance v. ground resistance.

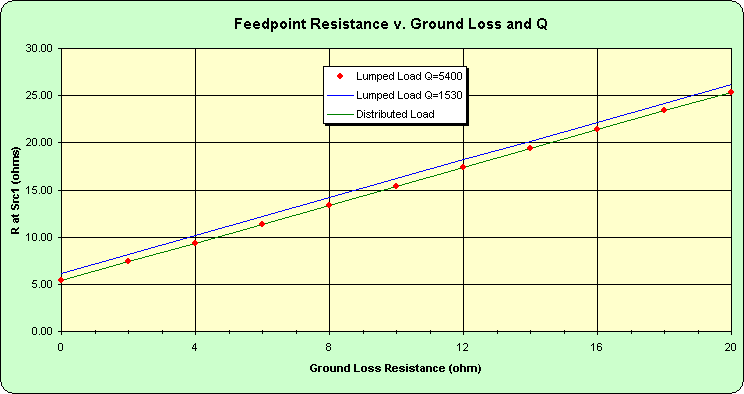
Figure 9.

The Short Loaded Dipole.

In anticipation of the inevitable sniping about whether or not the model of a monopole over perfect ground is a valid proof of anything, I also developed a model of a short horizontal loaded dipole. The radiator is simply twice as long as the monopole with loads placed midway between the feedpoint and the two ends. One minor difference is that the source wire is three segments long, rather than one segment used in the monopole cases. The model was operated in free space.

My expectation was that the behavior would be similar to the monopole, with the exception that the feedpoint impedance would be twice as large, the gain would be 3 dB lower and ground loss would be a non-issue. If Figure 10 is compared to Figure 2 and Figure 11 is compared to Figure 3 the correlation is obvious. The monopole current distribution is identical to one half of the dipole distribution.

Figure 10.

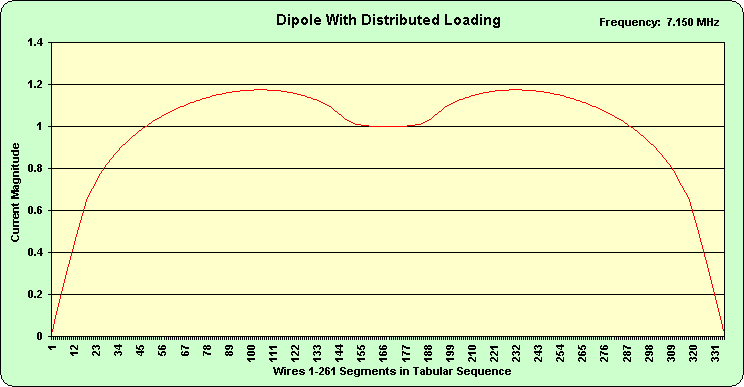
Figure 11.

Table 4 shows that the expected differences in the feedpoint resistances and gain between the monopole and dipole are realized.

Test Condition	Frequency (MHz)	Feedpoint R	Feedpoint X	Gain (dBi)
Distributed Coil Loading)	7.15	10.75	+j 0.0	0.72
Lumped load (Q = inf.)	7.15	10.12	+j 0.0	1.59
Lumped Load (Q=5400)	7.15	10.74	+j 0.0	1.33
Lumped Load (Q=1530)	7.15	12.38	+j 0.0	0.71

Table 4. 20 Foot Dipole, Copper Loss, Variable Q.

Acknowledgements.

I would like to thank Dan Maguire, AC6LA, and Danny Richardson, K6HME, for their review of this note and their thoughtful suggestions for improvements and also thank Dan for the great job he's done writing the MultiNEC program, without which I would not have tried to build the complex models. Any errors, omissions or otherwise dumb ideas presented are strictly the responsibility of the author.

Refereneces.

1. Hansen, Robert C, "Optimum Loading of Short Whip Antennas", IEEE Transactions on Vehicular Technology, Vol VT-24, No. 2, May 1975.

2. Devoldere, John, ON4UN, "Low Band Dxing, Third Edition, ARRL, Newington, CT., 1999.

3. Brown, Bruce F., "Optimum Design of Short Coil-loaded High-Frequency Mobile Antennas", The ARRL Antenna Compendium, Vol. 1, ARRL, Newington, CT., 1985.

Copyright ©2004 by W. D. Stewart. All rights reserved. Permission is hereby granted for linking to the original source material for non-commercial purposes. Reproduction of any or all of the material in print or any other medium without permission of the author is expressly forbidden.

Revised 1/26/2004