Filtros a Cristal
www.geocities.ws/danielperez www.qsl.net/lw1ecp Ing. Daniel Pérez LW1ECP
fb: Daniel Ricardo Perez Alonso contacto: danyperez1{arrroba}yahoo.com.ar
|
EN GENERAL |
|
|
FILTROS TIPO CELOSÍA (LATTICE) |
|
|
FILTROS EN ESCALERA (LADDER) |
* ¿Busca la resonancia de
un cristal con un generador de barrido?. Tendrá que usar una velocidad de
barrido baja y/o bajar el rango barrido: si se exageran los kHz/segundo la
respuesta se deformará y correrá groseramente, y en un caso extremo ni se
percibirá dónde resuena.
* En receptores de doble conversión el filtro de 1a FI debe tener un buen
rechazo en la frecuencia que dista 2 veces la 2a FI por arriba o abajo (según
cómo se ubique el 2o oscilador) de la 1a FI, para que no moleste lo que se
llama "2a imagen". En un receptor se pensaba usar una 1a FI de 70MHz,
y una 2a de 455kHz, un salto enorme que hace que el pozo de atenuación en el
filtro de 1a FI esté a una distancia relativamente muy cercana a la banda
pasante. Esto exige que se deba construir con circuitos resonantes con un Q
imposible de lograr con bobinas o resonadores helicoidales de dimensiones
razonables.
Se probó un cristal marcado 115,406MHz, que en realidad es de unos 23MHz
diseñado para operar en 5º sobretono, lo cual no impide usarlo en el 3º, o sea
69MHz. Bien, colocándolo así nomás en serie con un sistema de 75ohm se obtuvo
una atenuación fuera de banda muy pobre, por culpa de la C paralelo del
cristal. Haciéndola resonar con una pequeña bobina se mejoró bastante, e
incluso se pudo llevar la resonancia paralelo por debajo de la serie, 2 *
455kHz por debajo. Se eligió que sea por debajo para evitar la sucia respuesta
superior.
Aún así se necesitaba un pozo más profundo. Al tocar el encapsulado del cristal
con los dedos se notó que el pozo se hacía más profundo que dejándolo en el
aire o a masa. Se reemplazó el dedo por un preset conectado como resistor
variable, pudiendo llegar a producir un pozo virtualmente infinito, ver
{filtro69}:
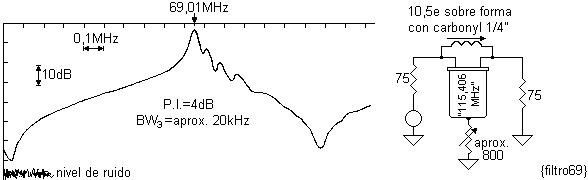
Lo que se está haciendo es similar a otros filtros notch en que la atenuación
no infinita debida al Q del inductor y capacitores se cancela con un resistor a
masa unido al punto medio del inductor, o una derivación capacitiva. Esto
último es lo que terminó siendo este caso: el encapsulado del cristal tiene una
cierta capacitancia con cada uno de los electrodos.
De todos modos, considerando que la profundidad del pozo en la frecuencia deseada
puede sufrir mucho por leves corrimientos en el inductor y el preset, es
recomendable agregar otro bloque similar a continuación, más que depender de
ajustes críticos.
* Cuando ya tenemos el
filtro, ¿cómo logramos que el circuito donde se injerte le presente las
impedancias terminales que resultaron?. De un lado probablemente tendremos el
drenaje del conversor; del otro, la compuerta o base del 1er FI. Ambas,
impedancias bastante distintas de las que necesitamos. Peor aún: si se usa en
un transceptor, las impedancias variarán según esté en el camino de transmisión
o de recepción. Y según cómo sea el 1er amplificador de FI, su impedancia puede
ser variable con el AGC. Y no hablemos de los conversores de recepción con
modulador doble balanceado a diodos, que son quisquillosos con la impedancia
que ven, para mantener baja la intermodulación.
Lo mejor es inspirarse en un circuito comercial. Se deberá cuidar la adaptación
en recepción usando transformación de impedancia con redes LC (no vaya por el
camino fácil de redes resistivas L o PI), y en transmisión sí se podrá
desperdiciar algo de señal resistivamente. Como no se conocen las impedancias
de entrada y salida de los dispositivos que rodean al filtro, se deberá hacer
varios tanteos mientras se observa la planicidad de la curva.
* ¿Cuánto de abrupto tiene que ser un filtro de SSB, o sea, cuántos cristales
se necesita?.
- En transmisión, no es imprescindible que se encargue de limitar el ancho de
la banda lateral deseada: este trabajo bien lo puede hacer un filtro en
frecuencias de audio. Su principal misión es suprimir la banda lateral
indeseada para no molestar al canal adyacente, pero este trabajo se desperdicia
si las etapas de potencia crean basura de intermodulación en un nivel mayor que
la banda suprimida. La cantidad de polos está determinada más bien por lo
abrupto que se quiere que sea el comienzo de supresión cerca de la portadora
(para las frecuencias de audio más graves). Para poder comercializar un equipo
debe respetarse la supresión que especifican las normas. Una vez lograda la
supresión requerida de banda indeseada, si el residuo de portadora está alto,
no ponga más cristales: mejore el balance del modulador, o posiblemente el
blindaje entre etapas. Como orientación, el filtro KVG XF-9A está pensado para
transmisión y es de 5 polos.
- En recepción debe filtrar todo lo que haya por arriba y por debajo del canal
deseado. Sin embargo, también hay un límite para lo que sea razonable exigirle
de rechazo: si el oscilador local tiene fuertes bandas laterales de ruido
(ruido de fase), éstas pueden batirse con los canales adyacentes y así permitir
que pasen en forma de ruido por el filtro. La versión para recepción (y también
transmisión) de KVG es el XF-9B, de 8 polos, a 6dB tiene 2,4kHz y es 1,8 veces
más ancho a 60dB (se dice Factor de Forma 6:60), y 2,2 veces a 80dB. Esto es un
lujo, pero en un diseño decente opino que no se debería usar menos de 6
cristales.
* Zócalos para cristales con patas para enchufar?. Triture un zócalo de
válvulas miniatura o noval y rescate las presillas. En la época de los FT243
correspondían los zócalos de válvulas octales.
FILTROS TIPO CELOSÍA (LATTICE)
*
Los cristales se comportan como circuitos sintonizados serie de altísimo Q, por
lo que resultan ideales para hacer filtros de alta selectividad. Sin embargo,
en la gran mayoría de los equipos de comunicaciones se necesita una curva de
respuesta más o menos achatada en la banda pasante, y un cristal solo tiene la
clásica forma de campana. Alguien preguntó por qué no ensanchar la respuesta
poniendo dos cristales de frecuencia ligeramente distinta en paralelo, como en
la figura {2xtales}:

La curva A es la que habría al tener colocado sólo el cristal A. Ídem para la
B. Para simplificar, los suponemos con capacitancia paralelo nula (sin
resonancia paralelo). Al poner a ambos a la vez, la curva resultante C sigue
pasando por los mismos puntos de atenuación cero de cada cristal, ¡pero en el
medio ocurre un pozo inesperado!. En ese punto, el cristal A, que es el de
menor frecuencia, está operando por encima de su resonancia, y por lo tanto se
porta como inductancia. Y al B le ocurre lo contrario, su comportamiento es
capacitivo. Por lo tanto tenemos dos reactancias de distinto signo en paralelo,
y en la frecuencia en que ambas tengan el mismo módulo pasará lo que pasa con
cualquier LC paralelo: máxima impedancia, en vez de mínima que era lo deseado.
Por lo tanto, lamentablemente, las curvas no se suman como parecería.
La solución correcta es invertir la fase con que se excita a uno de los
cristales con un autotransformador 1:1, que suele consistir en un toroide, con
buen acoplamiento entre bobinados. Ahora sí: en la frecuencia en la que
producía la anulación, ahora se comportará como si hubiese 1 solo cristal pero
con la mitad de reactancia. El nombre de esta configuración es "medio
lattice".
* Para los puristas: cuando un filtro consta de varios medio lattice en
cascada, y está bien diseñado, no es cierto que el 50% de los cristales sean de
una frecuencia y el otro 50% de otra: si se respeta los resultados de los
cálculos, debe haber mayor diversidad que 2 frecuencias, lo que suma más puntos
en contra del armador casero. El único lado donde vi un diseño verdadero fue en
Communications Engineering International Feb '80): era de 6 cristales, dos de
ellos iguales entre sí, otros dos iguales, uno distinto y otro distinto.
* Algunos artículos mencionan erróneamente que la frecuencia paralelo de uno
debe coincidir con la serie del compañero. En realidad, la estructura de un
medio lattice hace que cada cristal neutralice la capacitancia paralelo del
compañero (fenómeno muy deseable que lamentablemente no se produce en los
filtros en escalera), con lo cual desaparecen las resonancias paralelo.
* Experiencia no definitiva de filtro 1/2 lattice con cristales de banda
ciudadana, figura {lattice}:
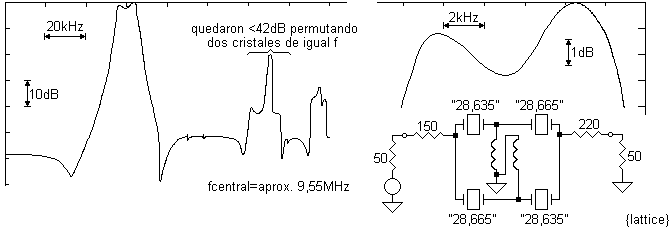
Desde aquí en adelante nos
concentraremos en los filtros en escalera, más convenientes para el armador
casero que los de celosía porque todos los cristales son de la misma
frecuencia.
* Para aumentar el ancho de banda de un filtro a cristal, entre otras cosas se
debe aumentar las impedancias de generador y de carga. Lamentablemente esto
empeora la atenuación en la banda rechazada, ver en {SpurXtal} pruebas hechas
con un filtro de 1 cristal al cual se le variaron las Z terminales:
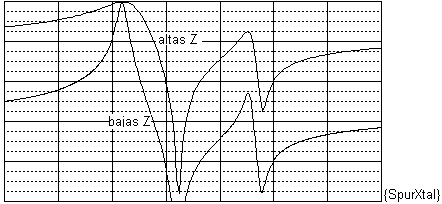
Es como que todas las porciones de baja atenuación se achatan contra la línea
de 0dB, y todo lo demás (lo indeseado) "sube", y la cercanía de la
frecuencia paralelo de los cristales molesta aún más.
Esto explica por qué es más problemático hacer un filtro a cristal para FM que
para BLU. Ejemplo: se quería hacer un filtro para transceptores de FM con
cristales de 10,24MHz, ver {asimetri}:

Faltan más secciones, pero la respuesta fuera de banda mostrada no es un buen
comienzo. Una mejor solución fue neutralizar las capacitancias como se ve en
{simetric}:
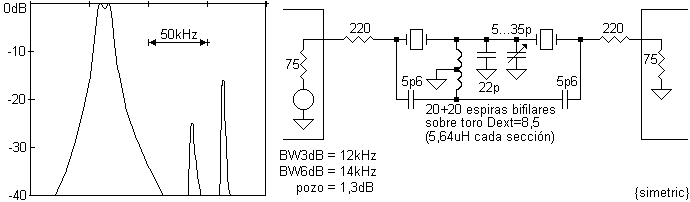
Mejoró el rechazo en general en la banda no pasante, y se simetrizaron también
los picos de la pasante, pero así no se resuelven las espurias. Éstas siguen
por un buen trecho, pero sólo importan las más cercanas a la frecuencia central
por ser las más difíciles de atacar.
Cabe esperar que las espurias de los demás cristales (cuando se construya el
filtro definitivo) no coincidan todas para que de ese modo los cristales
colaboren entre sí para matarlas. No sería mala idea que algunos cristales sean
de otro fabricante para que sea aún menos probable la coincidencia de espurias.
Otra forma de sacarse de encima la capacitancia paralelo es hacerla resonar con
un inductor, como en el filtro de 69MHz, pero para filtros del orden de 10MHz o
menos resultaría demasiado grande. En este caso, como hizo falta 5p6 en
contrafase para cancelarla, es porque la C paralelo interna también ha de tener
ese valor, y a 10,24MHz esto implicaría un inductor de 43uH para hacerla
resonar.
* (jul/04) Otra idea para que no moleste Cp, no probada en la práctica, es la
que vemos en {SinCp}:
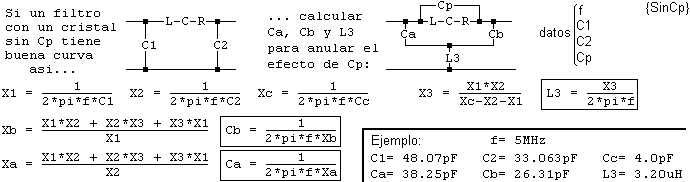
La simulación del circuito dio una eliminación total del efecto de Cp dentro de
la banda pasante. En la de atenuación, desapareció la resonancia paralelo que
había a unos 14kHz arriba, y aparecieron dos pozos mucho más distantes, en
150kHz a cada lado de la pasante.
Para poder aplicar esto es necesario dividir en dos cada capacitor a masa en
los nodos del filtro calculado con cristales sin Cp, y que los
capacitores en la entrada y salida del filtro sean a masa.
Esta técnica es la misma utilizada para neutralizar la capacitancia cátodo -
placa en un triodo con grilla a masa, con una inductancia en serie con la
grilla, aprovechando las capacitancias de ésta a cátodo y a placa.
* Un filtro escalera con n cristales iguales, con respuesta Chebyscheff, en
teoría debe presentar n picos en el pasabanda. ¿Cómo es posible, si la
frecuencia de todos los resonadores es la misma?. ¿No habría que usar sintonía
escalonada para ello, como lo son los lattice?. En {2picos} vemos qué pasa al
ir variando el acoplamiento entre dos resonadores idénticos:
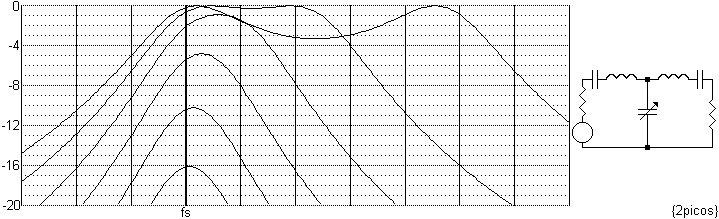
Con muy altos valores del capacitor intermedio, la respuesta total tiene un
único pico casi coincidente con la resonancia de cada sintonizado. En cada paso
consecutivo, el capacitor se va reduciendo a la mitad aumentando el nivel algo
menos de 6dB por paso al principio. Al superar el acoplamiento crítico, aparece
el par de jorobas aunque no se hayan tocado los resonantes. Créame que para 6 u
8 resonadores podemos tener 6 u 8 jorobas, no lo pienso demostrar. Además,
nótese que el centro del pasabanda se va desplazando: si en vez de una
capacitancia de acople se tuviese una inductancia, se correría para el otro
lado.
* Qué bueno sería que los cristales fuesen resonadores serie perfectos: sin
resistencia serie ni capacitancia paralelo. Los filtros en escalera serían
simétricos a cada lado de la banda pasante, y el ripple dentro de ella sería
fácilmente predecible. Como no es así, razonemos los efectos de los parámetros
residuales dentro de la banda pasante, para el caso de una escalera de dos
cristales, confirmado con una simulación en soft:
- La capacitancia en paralelo por sí sola, hace que el 2º pico sea más angosto.
- La resistencia serie sola, hace que el pozo en un doble sintonizado sea menos
profundo que lo previsto, o que no esté (además de introducir atenuación).
- Si hay capacitancia paralelo y además resistencia serie (lo que se da siempre),
ente ambas hacen además que el 2º pico tenga mayor atenuación que el 1º.
- El Q de los capacitores (o inductores) desde cada unión de cristales a masa,
no es tan importante como el de los cristales.
* En la QST de Noviembre de 1980 se publicó un método para diseñar filtros en
escalera con cristales de misma frecuencia, que no requiere medir e ingresar
los parámetros equivalentes del cristal. En vez de ello, propone armar un
filtro de prueba con dos cristales, hacer retoques, e introducir los valores resultantes
en fórmulas para extenderlo a la cantidad de polos deseada. El filtro de prueba
produce un valle de 1dB: el final tendrá en teoría también ripple de 1dB y
mismo ancho a 3dB que el de prueba.
En este vínculo se accede a un .BAS que automatiza un poco el proyecto, y
además contiene una sección independiente para calcular los parámetros a partir
de mediciones:
FilXtal.txt o bien: FilXtal.bas o bien: FilXtal.zip
(Se brinda en varios formatos por cualquier decisión inesperada que tome el
navegador). Si elige el .txt, tras abrirlo con un clic, guárdelo "Como
Archivo de Texto", luego cámbiele la extensión a .BAS.
El archivo se corre bajo DOS con el QBasic.exe, que venía con las últimas
versiones de MS-DOS .
El artículo original también fue traducido y adaptado en la Electrónica
Práctica de Diciembre de 1983.
Veremos su aplicación con un par de ejemplos.
* Experimento de filtro para BLU con cristales de 8867,238kHz (surplus
de antiguas conversiones PAL-B a N).
(22/jul/2000 con correcciones de julio/2004: se eliminó el elevar al
cuadrado en recálculo de C)
Se comenzó por medir las frecuencias serie. Eran 27 unidades, y resultaron
estar entre 8863,04 y 8863,45MHz:
,04 ,05 ,08 ,09 ,11 ,12 ,13 ,13 ,14 ,15 ,15 ,15 ,16 ,22 ,25 ,27 ,27 ,27 ,28 ,30
,30 ,32 ,32 ,34 ,36 ,44 ,45
Se eligió el grupo ente 8867,13 y 8867,15.
Se editó el programa para tener fo=8,863MHz y N=6. Se buscaba tener 2338 a
-3dB, para que a –6dB se tengan 2400Hz (según una tabla de Chebyscheff con
ripple de 1dB). Esto fue sólo por manía perfeccionista: el error por no
distinguir entre el BW a 3 o a 6dB sería menor que el del método.
Comenzando con los capacitores recomendados de 33pF, el programa especificó
resistencias terminales de 333ohm. Esto significa, por ejemplo, que si el
generador tiene una salida de 50ohm habrá que agregarle 283ohm en serie; y la
carga puede ser directamente 333ohm si el detector es de impedancia bien alta
(si no, recurrir a redes resistivas que aseguren la Z necesaria).
Se armó, y dio un BW de 5360Hz, demasiado alto.
El nuevo intento fue con capacitores de 33 * ( 5360 / 2338 ) = 75,6pF. El
programa calculó resistencias de 146ohm, se midió el nuevo BW y se recalcularon
las R y C según indica el programa. Cabe destacar que en la QST esta división
de anchos de banda aparece elevada al cuadrado, pero en mi experiencia omitir
el exponente permite una convergencia más rápida.
El último intento fue con 105pF y 104,8ohm, y se midió 2360Hz. Ok. Se armó lo
que se muestra en {Xtal8867}:
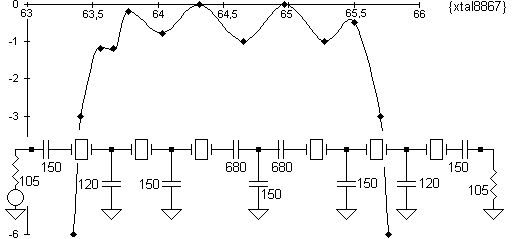
(Debería haber 6 picos para un filtro de 6 cristales, pero es común que alguno
de los extremos quede disimulado en las imperfecciones del filtro real).
Si se desea medir la banda atenuada por debajo de 80 o 90dB, no sólo deberá
cuidarse religiosamente el bindaje del filtro, sino también probablemente se
deberá agregar un post amplificador dentro de su misma caja para que no moleste
el acoplamiento desde la entrada.
Bueno, ya tenemos el filtro. Ahora veamos cómo podemos mantener la filosofía de
seguir usando un único modelo de cristal también para la generación de
portadora.
Para generar BLI (sin considerar la probable inversión en el conversor), el
oscilador trabaja por encima de la banda pasante, lo cual es fácil: la
frecuencia resulta cercana a aquella para la que se diseñaron los cristales en
un oscilador Pierce. Pero para BLS, habrá que forzar al cristal varios kHz
hacia abajo, aproximadamente por donde está la resonancia serie. Esto se logra
agregando un inductor en serie. En el oscilador A) de {osc8867} se probaron
varias cosas en el lugar "Z" en serie con el cristal, desde 5pF hasta
varios tipos de bobinas. En B) se aprecia que se puede forzar desde 6,5kHz por
arriba hasta 28kHz por debajo de la frecuencia nominal, mucho más allá de lo
que necesitamos (guiarse por la curvita del filtro dibujada sobre la escala), o
sea que podemos aprovechar aquí los cristales más dispersos del lote. Con menos
de 5pF deja de oscilar. Y si se abusa de la inductancia en serie, el circuito
degenera en un vulgar Colpitts: la frecuencia terminará siendo gobernada
únicamente por el inductor, y la capacitancia eléctrica del cristal, perdiéndose
totalmente el efecto estabilizador del mismo.
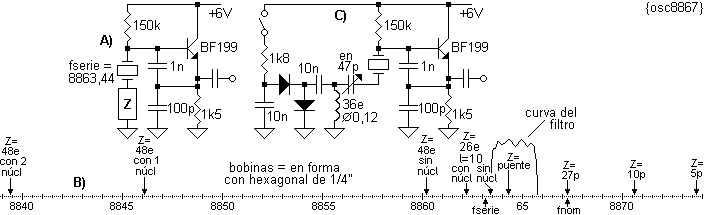
Con estos datos también puede armarse un oscilador con el rango necesario para
levantar la respuesta del filtro en la banda atenuada.
Sólo queda por hacer una elección:
- un oscilador independiente para BLS y BLI, uno c/u con su respectivo cristal,
uno con un trimmer y el otro con una bobina variable en serie. O bien:
- la solución C): con los diodos conduciendo la bobina queda cortocircuitada y
se ajusta el trimmer para una BLI correcta, y al dejarlos en el aire se ajusta
la bobina para la BLS.
Para una producción seria, la 2a opción debería ensayarse en cuanto a
estabilidad térmica. Si da Ok, más allá de ahorrar un cristal, simplifica la
conexión al resto del circuito.
Anécdota: el oscilador variable que se utilizó para barrer manualmente era un
modelo de cómo NO debe ser la construcción en RF: en el aire, sin blindajes.
Parece que la RF se irradiaba hacia todos lados, y la frecuencia del oscilador
¡era modulada por los diodos de la fuente!. Se notaba como una modulación de
amplitud de 100Hz en la señal vista con el osciloscopio, sólo cuando se situaba
en las empinadas laderas del filtro, con lo cual se convertía esta FM en AM, y
por lo tanto era denunciada por el detector.
* Lo siguiente es un ejemplo que NO funcionó:
Se tenía un lote de resonadores Murata B456 rescatados de decodificadores FM
estéreo de auto radios, donde se usa para un VCO enganchado en 456kHz, 24 veces
el tono piloto de 19kHz. Sin embargo, la frecuencia serie medida es de unos
434kHz, y la paralelo es 20kHz más arriba. Se pensó en emplearlos para un
filtro escalera de SSB. Ver {456}:
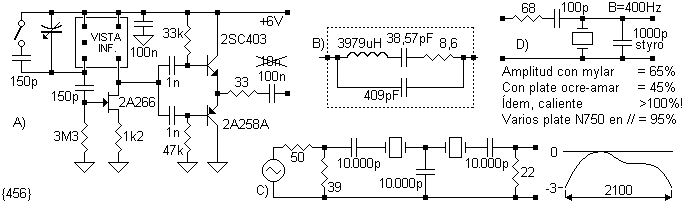
En A) se ilustra el fiel generador que me acompañó desde el Industrial. Utiliza
una osciladora 10x10 tipo Spica, pero sintonizada con la sección de antena del
tándem, oscilando de 540 a 1600; y al colocarle un capacitor fijo en paralelo
se tiene 386 a 530, con lo cual se puede barrer con comodidad razonable el
rango de interés. Entrega unos 1,8V pico a pico a circuito abierto, presentando
una impedancia de salida de 50ohm. La salida complementaria permite bajas
impedancias de carga sin que recorte. Ajustar uno de los resistores de base
para 50% Vcc en los emisores.
Como detector se empleó un osciloscopio. El tubo tiene una retícula grabada
internamente, con +/-4 divisiones verticales. Se agregó una escala en dB
escribiendo con marcador indeleble fino sobre el vidrio (desde afuera, no había
más remedio). Las marcas de 0 -1 -2 -3 -6 y -infinito se dibujaron en las
alturas de 4 3,6 3,2 2,8 2 y 0 divisiones. Para evitar errores de paralaje se
inscribieron las seis mientras mantenía mi cabeza inmóvil, y antes de efectuar
cada medición volvía a ubicar mi cabeza en altura y distancia para hacer
coincidir las marcas extremas.
Para apreciar cualitativamente la forma de la curva, se la puede
"barrer" girando rápidamente el generador, teniendo el osciloscopio
en barrido "normal" y con el umbral como para disparar cuando se
llega a un cierto nivel de RF al acercarse a la banda pasante.
Cada vez que se necesitaba normalizar amplitud, se giraba el ajuste variable de
sensibilidad hasta hacer coincidir el pico de la onda con la marca de 0dB,
cuidando que el pico negativo coincidiese con la división inferior.
En B) se muestran los parámetros calculados, a simple título informativo.
Al medir la tensión de entrada molestaron las armónicas del generador, ya que
en resonancia se atenúa la fundamental y éstas no.
Para no alargar este punto, mencionemos que para esta tecnología de resonadores
y a esta frecuencia tan baja el valor inicial de 33pF resultó bajísimo. Un
valor más realista resultó ser 10nF. En C) vemos el circuito correspondiente y
su respuesta, cercana al ancho deseado. ¿Qué vemos de malo?. No hay dos picos
definidos, indicando que el Q propio de los resonadores es insuficiente. Si se
hubiese insistido, un filtro final de 6 polos resultaría con la respuesta
groseramente redondeada.
Anécdota: el oscilador empleado no es limpio en cuanto a armónicas, lo cual
ocasiona un gran error al medir la resistencia serie: como las armónicas no son
rechazadas, el detector las detectará haciendo creer que Rs es mayor que la
realidad. Afortunadamente, como se estaba usando un osciloscopio como detector,
fue fácil comprobar que en resonancia casi todo lo que se medía eran armónicas.
Se solucionó agregando una bobina de FI con sintonía ancha, antes del
osciloscopio.
Se comprobó que los resonadores que se consiguen como repuesto para los
controles remoto tienen mejor Q. Tal vez se prueben en un futuro. Los
siguientes se midieron así: conectados a masa, excitados desde 50+68ohm, Rserie
medida por sustitución:
|
|
fo [kHz] |
Rserie |
B(+3dB) [Hz] |
f// - fserie [kHz] |
|
CSB455E (remoto) (Philco) |
442,8 |
7,1 |
160 |
15,5 |
|
ZTB455E (remoto) (Laury) |
440,1 |
8,6 |
255 |
18,1 |
|
B456 (decodificador estéreo) (Philco) |
434,4 |
9,5 |
400 |
20 |
Eso sí: tenemos el problema
de los voluminosos capacitores requeridos para el filtro. Los cerámicos del
orden de la decena de nF están hechos más bien para acople y desacople: no son
de buen Q y mucho menos son estables con la temperatura, por lo que debería
usarse los difíciles de conseguir styroflex (poliestireno), o a lo sumo mylar
(poliéster). En D) se probó hacer un pasabanda con un resonador resonando en
paralelo con un styroflex. El nivel obtenido se tomó como referencia 100%. Al
reemplazarlo sucesivamente por un mylar, un cerámico de mediana K y un paralelo
de varios NPO se tuvieron los niveles en resonancia indicados. La sorpresa se
dio cuando se calentó el cerámico de mediana K con el soldador para ver el
corrimiento de frecuencia: lo que se halló fue un aumento inesperado de su
calidad, pareciendo superar a la del polistirene. Debe tratarse de un error en
la normalización, pero de todos modos ilustra sobre la dependencia térmica de
estos componentes.
* No sólo es de radioaficionados usar cristales de TV color: el analizador de
espectro Advantest R4131DN (un instrumento serio) usa cristales de NTSC para
los filtros más angostos.
Los resonadores de frecuencias cercanas a 455kHz son comunes en las casas de
componentes, gracias a que los fabricantes de controles remotos se olvidan de
pegarlos a la plaqueta y terminan cortándose por vibración tras varias caídas
del remoto.
* (dic/08) Aquí se puede bajar un muy buen shareware para cálculo de filtros convencionales
y también con cristales en escalera, gratis y totalmente funcional:
www.aade.com/download.htm
Incluye abundante literatura sobre diseño de filtros a cristal. Un comentario
se puede hallar en: www.electronics-tutorials.com/filters/filter-software.htm
* (jul/04) Si se desea simular un pasabanda extremadamente angosto (como un
filtro a cristal) en Spice u otro simulador, deberá verificarse si con
resonadores sin pérdidas se puede obtener pérdida nula. Una versión 1987 de
MicroCap daba muchos dB de pérdida inexistentes, tal vez debido a que la
precisión de la matemática utilizada no era adecuada para manejar cantidades
reales e imaginarias que distan muchos órdenes de magnitud entre sí. Y las
versiones de Electronics Workbench que probé no permiten un barrido angosto.
Inesperadamente, la mejor herramienta que encontré se llama TCAP.BAS, era parte
de una biblioteca de dominio público anunciada en RF Design, firmada por el Dr.
Allen Katz en 1986. Estaba escrito para GWBASIC (con números de línea). Tras
agregarle la declaración de doble precisión, creación de un XLS con los
resultados, y algunas modernizaciones de QBasic, brindó una exactitud asombrosa
en las simulaciones. El mayor inconveniente es que se basa estrictamente en
texto. Si le interesa, está en Tcap.zip junto con el original
(TCAP-IBM.BAS), y archivos .CAP generados en una prueba "virtual" de
FILXTAL.BAS. Virtual?. Le cuento:
En el soft de AADE se había diseñado un filtro de 5MHz (considerando Rs y Cp de
los cristales) cuya curva, graficada por el mismo programa, parecía más fea que
la de un filtro real, y se dejó de lado. Pero se aprovechó su modelo de los
cristales para "armar" el prototipo de FILXTAL dentro de TCAP. En
TCAP01 están los valores y el esquema (véalo con un editor de texto) del primer
prototipo, con 33pF, no se usó Rs ni Cp. Se midió el BW graficando en Excel el
XLS generado. Tras corregir los capacitores se generó TCAP02 que dio ya mismo
el BW deseado. En TCAP03 se armó el filtro de 6 cristales. En TCAP04 se ve el
efecto de agregar las Rs: se agregó una pérdida de 1,2dB en el centro de la
pasante más un redondeo de los bordes. Pero en TCAP05, considerando las Cp, la
deformación es aún más seria: casi desaparece la joroba superior, y se angosta
bastante la banda.
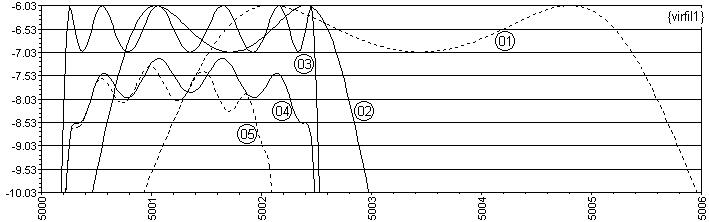
{virfil1} es una vista expandida de las bandas pasantes. Las bandas atenuadas
se aprecian en {virfil2}. En cuadro aparte se ve en profundidad (300dB!) la del
caso 05, destacándose la resonancia paralelo. En la práctica, la atenuación
final difícilmente supere los 100 o 120dB por los sempiternos acoplamientos
indeseados. El modelo de los cristales tampoco incluye las resonancias
espurias.

La forma en que se sucedieron las generaciones de curvas fue sólo para ilustrar
fehacientemente el efecto de las parásitas; en un diseño serio se deberían
considerar ya desde el prototipo.
Aclaración: nótese que el tope del eje de decibeles es -6 (en rigor,
-6,02=20log(0,5) ). Pero esto equivale a una pérdida de INSERCIÓN de 0dB,
pérdida agregada nula.
* ¿Alguien probó con usar inductores en vez de capacitores entre los
cristales?. Esto, si funciona, tendría la ventaja de hacer que el pasabanda
quede por debajo de las resonancias serie, con lo cual quedaría un poco más
lejos de la distorsionadora resonancia paralelo, y además se abarataría un poco
el filtro. También se simplificaría la neutralización de la C paralelo de los
cristales como se vio en la figura {simetric}, aprovechando las mismas bobinas
para agregar un secundario y así obtener la señal en contrafase. El programa de
AADE prevé la variante con bobinas.
<eof>