




Milazzo, Carol F., KP4MD, "Programming for Automated Satellite Communication", ham radio, Vol 11:6, June 1978, pp. 68-71. Algorithm for a satellite locating program for the Texas Instruments SR-52 programmable calculator.
Following the lead of Ball in February ham radio, author Milazzo has also derived the equations for tracking Oscar-emphasis in this case has been placed on developing a program suitable for use with the Texas Instruments calculators which use algebraic notation
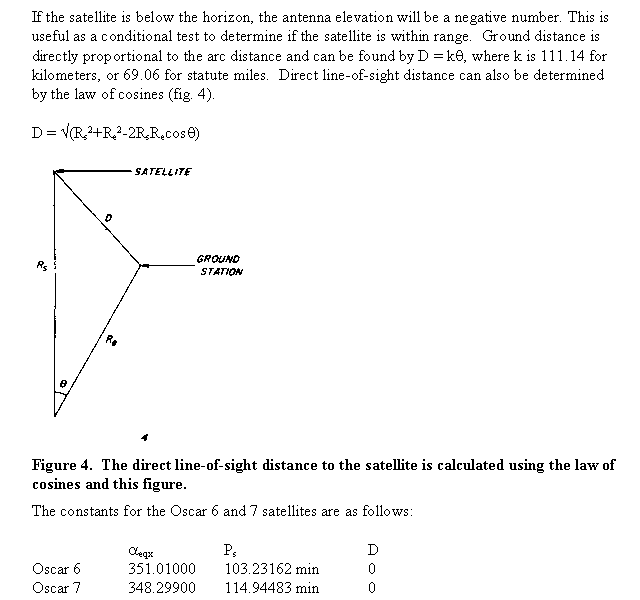
Of primary importance in satellite communication is the required antenna orientation and the time during which the satellite is available from the ground station. Such information increases the dependability and efficiency of satellite use. Presently, the means of obtaining this data is widely available due to the increased popularity of low-cost programmable calculators and minicomputers.
Previous articles have dealt with the prediction of equatorial crossings.1-2 These offer few advantages since such information is published monthly and interpolation of this data is easily accomplished. Other articles do offer more useful information but require the use of slide-rule type devices which are imprecise and incapable of being interfaced with station equipment.3-4
This article presents a series of equations for determining the exact position of any earth satellite that approximates a circular orbit, at any given time. The calculations are useful for manually or automatically tracking a satellite, for preparing tables for future reference, or for alerting the operator when a satellite is approaching. This algorithm has been used to prepare programs for the Texas Instruments SR-52 calculator, but can be programmed for other calculators and computers as well.






Due to the complexity of the calculations required, the program is divided into two modules.* The first module enters the appropriate reference and constant information into the data memory, while the second module computes the satellite's position and direction in terms of azimuth and elevation from a specified ground location. In the second module, the desired time is entered from which the calculator displays the elevation angle, indicating if the satellite is within range. The azimuth and arc distance can then be called from the calculator. To facilitate the tabulation of the results, one key has been programmed to advance or reverse the position of the satellite by a desired number of minutes. The following example demonstrates the use of the program.
The antenna aiming data for the first Oscar 7 pass of August 1, 1977 is desired. The first program card is read into the calculator, and the R/D switch is placed in the degrees mode. A reference orbit from January 1, 1977 is available. The satellite is found to cross the equator at 77.0 west longitude at 0148:49 on January 1. The station coordinates are 1825' north latitude and 6558' west longitude. Therefore, the following key sequence is executed:
enter press display 7 A 7 (satellite #) 1 B' 2400 (enter date) 148.49 B 1548.82 77.0 C 77. 18.25 D 18.42 65.58 E 65.97
The second card is now read into the calculator. Since the exact time of acquisition is not known, a rough estimate can be made based on the fact that the satellite travels at about 3 degrees per minute and it must be within 36 degrees of the station to be heard. First, determine if the satellite is within range at 0000 GMT on August 1(213th day of 1977).
enter press display
213 A' 511200 (enter date)
0 A -9.23 (enter time/disp. elev.)
C 45.8 (disp. distance)
The negative value for elevation showed that the satellite is below the horizon at 0000 GMT, while pressing C showed that it is about 10 degrees beyond the 36 degree range limit. If the satellite is approaching, it will take about four minutes to come within range. Advancing the satellite four minutes produces:
enter press display
4 E 2.25 (elevation)
B 147.8 (azimuth)
C 33.4 (distance)
The satellite can be advanced at one minute intervals to produce a listing for this pass.
time elev. azim. distance 0004 2.2 147.8 33.4 0005 5.7 146.2 30.3 0005 9.4 144.3 27.2 0007 13.5 142.0 24.2 0008 18.1 139.0 21.2 0009 23.4 135.1 18.3 0010 29.3 129.8 15.5 0011 35.9 122.4 12.9 0012 42.7 111.5 10.6 0013 48.7 95.5 8.8 0014 51.6 74.3 8.0 0015 50.1 52.1 8.5 0016 44.8 34.3 9.9 0017 38.1 22.0 12.1 0018 31.3 13.6 14.6 0019 25.2 7.8 17.4 0020 19.7 3.7 20.3 0021 14.9 0.6 23.3 0022 10.6 358.1 26.3 0023 6.7 356.2 29.4 0024 3.2 354.7 32.4 0025 0.0 353.5 35.6
Results from this program have been compared with published equatorial crossing data, with the predicted coordinates accurate to within one tenth of one degree for both Oscar 6 and Oscar 7. This, for one year from a single reference orbit.
The user instructions for the program are straightforward, but the following hints are useful. A date need not be entered if the reference and unknown orbits occur within the same day. When entering a date, it must always be entered before the time. The dates of the reference and unknown orbits must be either within the same month, or else each day of the year must be assigned a consecutive number. The "+ Time" key may be used to reverse the satellite's position by merely entering the negative value of the desired number of minutes. Finally, if you desire to enter a new time without using the "+ Time" key, it is necessary to re-enter the date (if used) before entering the new time. I can supply the program on magnetic cards with any station coordinates and reference orbit recorded for the cost of $5. This includes program documentation.
By using the preceding equations, any person can build his own computerized satellite tracking station by interfacing a digital clock and station controls to a microcomputer. Even without a computer, this program offers valuable, accurate information for any satellite operator.
*A copy of the program is available by sending a self-addressed, stamped envelope to ham radio, Greenville, New Hampshire 03048.
Originally published in ham radio, Vol. 11:6, June 1978, pp. 68-71.