Upon running the program, the user must first specify if a low-pass/high-pass or a band-pass/band-stop filter is desired. If the low-pass high-pass design is chosen, the user must then specify two frequencies in Hz, each followed by the respective attenuation desired (this may be a very small value but never exactly zero). The source resistance must then be specified. The program will then calculate and display the minimum number of branches required for the specifications, and request if the first branch is to be series or shunt. The program will then calculate all required component values rounded to 3 significant digits and displayed in the most common units. The rounding feature may be eliminated by changing statement 830 to "LET X1=X". The program will then provide a table of attenuation vs. frequency for any specified range and increment of frequency.
If the band-pass/band-stop design is selected, the process is similar except that first the center frequency of the filter must be specified, and then two frequency bandwidths with their respective attenuations. These filters are geometrically symmetrical, i.e. the center frequency is not exactly the arithmetic average of the limit frequencies of any bandwidth. The relationship is really fc=SQRT(f1xf2).
The given examples demonstrate the use of this program. The first filter designed is a band-stop filter for 11 meters, providing 20 dB attenuation over 26.965 to 27.405 MHz (bandwidth of 440 kHz) and only 1 dB attenuation over 26.37 to 28.0 MHz (bandwidth of 1.63 MHz). This type of filter may be designed for the input of a linear amplifier to prevent operation on the 11 meter band while permitting operation on the 10 meter band. This filter requires only 3 branches (total of 6 components), and its response over 26 to 28 MHz is shown in the printout.
The second example shows design of a low-pass filter, such as used for TVI suppression.. An attenuation of 30 dB is specified at 54 MHz, while a loss of 1 dB is specified at 28 MHz. This filter would require 7 elements, and its response over 5 to 55 MHz is shown in the table.
This program offers the radio amateur the ability to synthesize modern Butterworth filter circuits with all calculations performed by a computer. All previously published articles in amateur magazines on this subject present tables of normalized filter values or only a few "typical" values for certain common frequencies. This program offers the full flexibility possible by using the original formulas for synthesis of Butterworth filters. It is possible to write such programs for Chebyshev and other modern filters, and these will require slightly more complicated formula derivations. This is one of the author's future projects for programing on the Timex Sinclair 1000.
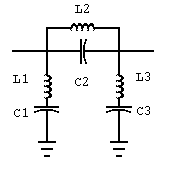
CENTER FREQUENCY 27.185 MHZBANDWIDTH FREQUENCY ATTENUATION (DB) 440000 20 1630000 1 RESISTANCE (OHMS): 50 NO BRANCHES=3 1ST EL. (SERIES=1, SHUNT=-1) -1
BRANCH 2 SERIES
C 2 = .00122 UF IN PARALLEL WITH
L 2 = .028 UH
BRANCH 3 SHUNT
L 3 = 6.12 UH IN SERIES WITH
C 3 = 5.6 PF

Figure 1. 27 MHz bandstop filter.
FREQUENCY RANGE (HZ) LOWER LIMIT: 26000000 UPPER LIMIT: 28000000 IN STEPS OF 100000 FREQUENCY HZ ATTENUATION DB 26000000 0.10273635 26100000 0.17496129 26200000 0.31124634 26300000 0.580021 26400000 1.1286903 26500000 2.2531149 26600000 4.4293654 26700000 8.1439241 26800000 13.677399 26900000 21.404383 27000000 32.684123 27100000 52.995257 27200000 98.242908 27300000 45.214405 27400000 28.962848 27500000 19.105926 27600000 12.18576 27700000 7.2439357 27800000 3.9779707 27900000 2.0779733 28000000 1.0813628
FREQ MHZ ATTENUATION (DB) 28 1 54 30 RESISTANCE = 50 OHMS NO. BRANCHES=7 1ST EL. (SERIES=1, SHUNT=-1) -1
BRANCH 2 SERIES
L 2 = 0.322 UH
BRANCH 3 SHUNT
C 3 = 186 PF
BRANCH 4 SERIES
L 4 = 0.516 UH
BRANCH 5 SHUNT
C 5 = 186 PF
BRANCH 6 SERIES
L 6 = 0.322 UH
BRANCH 7 SHUNT
C 7 = 45.9 PF

Figure 2. Low-pass filter.
FREQUENCY RANGE HZ LOWER LIMIT: 5000000 UPPER LIMIT: 55000000 IN STEPS OF 5000000 FREQUENCY HZ ATTENUATION DB 5000000 0 10000000 6.1681405E-7 15000000 .00018030821 20000000 .010107901 25000000 0.22420646 30000000 2.2537036 35000000 8.3804788 40000000 15.930315 45000000 23.001189 50000000 29.390423 55000000 35.181716