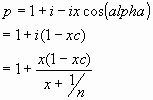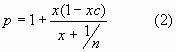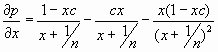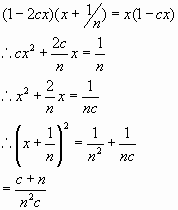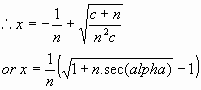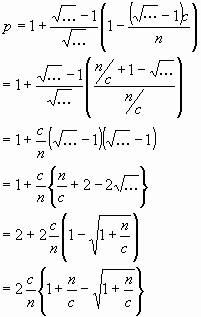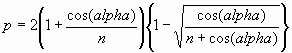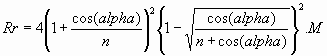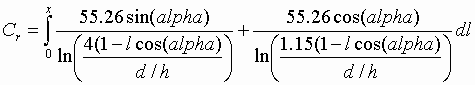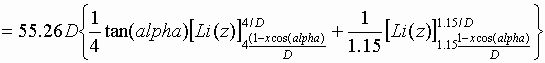Umbrella Antennas for LF
John Sexton, G4CNN
After reading the excellent web page of ON7YD,
where the essential formulae are given, I realised that I had enough information
to calculate the best shape for an Umbrella Antenna. This is a vertical
with top loading wires, which descend to a certain fraction of the height.
The question is just what that fraction should be for greatest Radiation
Resistance.
It is assumed that the antenna is small compared with a wavelength,
which will usually be the case for an Amateur
antenna. This means that on any continuous segment of the antenna,
the voltage will be approximately constant and that
the current will decrease linearly. The rate of decrease depends upon
the voltage and the capacity to ground of the segment.
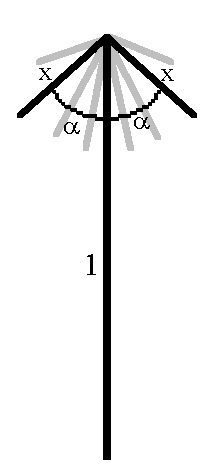
We take the height of the vertical as unity and the length of each
rib as x, i.e. as a proportion of the vertical height.It is supposed that
there are n ribs all of the same length and all inclined at an angle alpha
to the vertical.
The antenna current is taken as unity at the base and decreases approximately
linearly to a value i at the top of the vertical. With no ribs,
i
is zero. The current then divides equally between the ribs and decreases
linearly to zero at the end of each rib.
Increasing the length of the ribs increases the capacity of the top
hat and therefore increases the value of i and as a consequence
increases the Radiation Resistance, Rr. However the current down the ribs
has a downward vertical component which decreases Rr. As the length x
of the ribs is increased from zero, Rr first starts to increase. As the
length increases Rr reaches a maximum value and thereafter decreases. The
purpose of the analysis below is to determine the optimum value of x
which produces the greatest value of Rr for a given number of ribs, n,
and a given angle, alpha. We will then explore the effects of increasing
n
and changing alpha.
If alpha were 180°, one rib would constitute an extension of the
vertical and the value of i can be calculated remembering that the
current decreases linearly from 1 to zero along the entire length of the
antenna. In this case we would have:
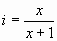
When the ribs are horizontal or downward sloping, they contribute more
to the top hat capacity than the single upward extension of length x
provided that they are well separated. (This of course will not be true
at the centre, but we will come to that later.)
From the formulae for the capacity of horizontal and vertical wires,
it has been shown that for typical amateur antennas, 1 metre of horizontal
wire contributes approximately 5 pF per metre and 1 metre of vertical wire
contributes approximately 6 pF per metre. These figures are practically
the same and therefore for n ribs we can deduce that the value of i
for practical purposes is given by:
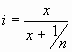 (1)
(1)
A more detailed analysis will be given later.
Each antenna segment contributes a component of the Radiation Resistance
in proportion to the square of the product of the average current flowing
in the segment and the length of the segment.
If we take the Radiation Resistance of a vertical monopole as M, the
Radiation Resistance of the umbrella antenna can be written:
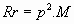 and we can calculate p to
make this a maximum.
and we can calculate p to
make this a maximum.
We consider the antenna as consisting of 1 vertical element and n ribs.
The average current in the vertical element is 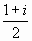 ,
and since the average current flowing in a monopole is
,
and since the average current flowing in a monopole is 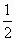 ,
the ratio is simply 1 + i.
,
the ratio is simply 1 + i.
Similarly the average current flowing in all of the n ribs taken
together is 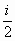 and
as a ratio to the monopole this is simply i. But this current is
downward and has a vertical component i.cos(alpha). Remembering
that the length of the vertical is 1 and the length of each rib is x,
it follows that:
and
as a ratio to the monopole this is simply i. But this current is
downward and has a vertical component i.cos(alpha). Remembering
that the length of the vertical is 1 and the length of each rib is x,
it follows that:
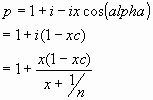
i.e. 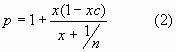
To find the value of x for which this has a maximum, we differentiate
with respect to x and solve for the derivative = 0.
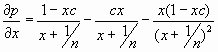
and this is zero when:
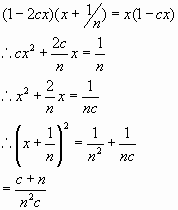
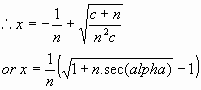
If we now substitute this value of x in equation (2), we obtain
a maximum value for p:
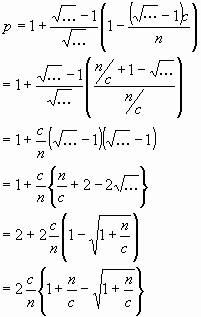
i.e. the maximum value for p is:
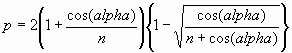
and the value of the Radiation Resistance is
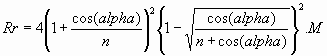
I have tabulated these results for some values of n and alpha using
Microsoft Excel and include these results below:
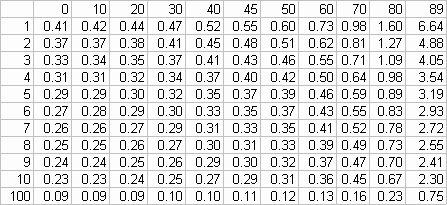
Table of values for x
Values of alpha from 0 to 89° horizontally and Values of n vertically
Note that there is no maximum for alpha = 90°, the longer the radials
the better, short of a quarter wavelength.
It can be seen that the greater the angle, the longer the ribs can be
and the more ribs the shorter they must be.
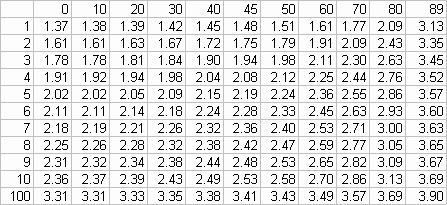
Table of values for Rr/M
Values of alpha from 0 to 89° horizontally and Values of n vertically.
Note that the maximum that can be achieved is a factor of 4 (6 dB) better
than a Monopole.
One can either use greater angles or more ribs to approach the theoretical
maximum value of Rr.
Assumptions
The above formulae were obtained using formula (1) which assumed that
the capacity per unit length of the ribs was the same as that for the vertical
element. More accurately we may proceed as follows:
The capacity in picofarads per unit length of a horizontal wire at a
height of h metres is given by the formula:
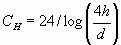 where d
is the diameter of the wire in metres
where d
is the diameter of the wire in metres
and the formula for the capacity in picofarads per unit length of a
vertical wire at a height h metres is:
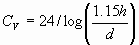 .
.
If we change the formulae to use the natural logarithm rather than
logs to the base 10, these formulae become:
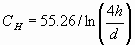 (3)
(3)
and
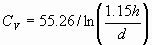 (4)
(4)
Therefore for a rib of the umbrella we may calculate the capacity as
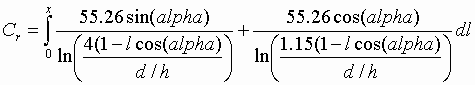
Here h is the actual height of the vertical in metres
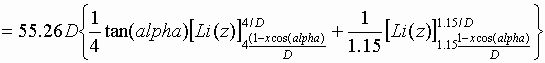
where D stands for d/h.
The function Li(z) is the Logarithmic Integral and is tabulated. e.g.
Jahnke und Emde, Tables of Functions.
Calculations with typical values of x, h, d and alpha show that Cr
does indeed take values of the order of 5 or 6 pF per metre, confirming
the approximate correctness of the formulae. Calculations with small values
of alpha tend to give larger values for Cr, but I believe that these are
invalidated by the closeness of the ribs to the vertical and to one another.
Back to Home Page

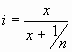 (1)
(1)