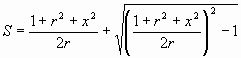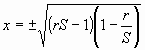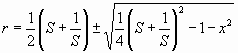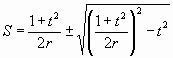HOW TO SOLVE YOUR ANTENNA MATCHING PROBLEMS
John Sexton, G4CNN.
Reprinted from Echelford Amateur Radio Society Newsletter for November
1978.
Introduction.
In January 1977 there appeared in RADCOM an article by G6XN extolling
the virtues of the Smith Chart. Having recently acquired a programmable
calculator with magnetic cards for permanently keeping programs I decided
to have a go at discovering the underlying 'Maths' and writing programs
to do the job.
I succeeded and now have a suite of programs on just 2 cards which will
do all that a Smith,chart will. I realise that Maths is not everybody’s
cup of tea, but it is really much easier to get the right answers this
way. Trying to find the correct point on the chart is not very easy, especially
as you get older and your eyes are not what they once were.
However the over-riding reason for doing it this way is that Smith charts
are not easily available:
A Non-calculator method.
Let me allay your fears. I am not about to give the details of a
computer program. It turned out that the calculations are not.very difficult
and if you can remember how to do squares and square-roots, this is enough.
So here we go.
Some Basics.

If the transmission line has an impedance Zo and if the load has an
impedance Zo then the line is matched and the SWR is 1. However long the
line is (assuming no losses) the generator (transmitter) will see
a constant non-reactive resistance Zo. (e.g. 75 ohms).
But if the load is reactive, or not equal to the characteristic
impedance of the line, then the line is not matched and will have
standing waves on it. They have a pattern which repeats every half wavelength.
Provided that the line is not too lossy and that the transmitter can
cope, the load will get as much power as in the matched case. If
the load is an antenna it will radiate just as much power.
The reasons for keeping the SWR down are:-
1. High voltages and currents can be generated at points on the line
causing insulation problems.
2. The transmitter probably can't cope with very much reactance nor
a load which is too far from its nominal output impedance.
3. At high frequencies and high SWR'S, line losses can be significant.
Wavelength in Feet = 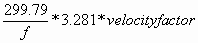
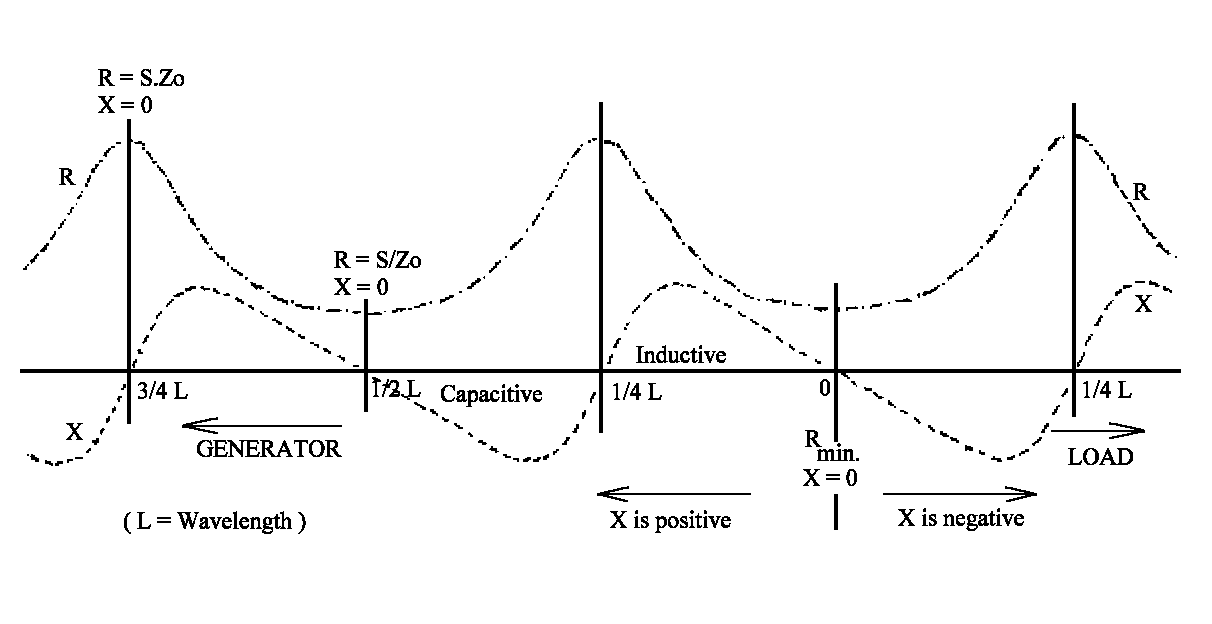
The diagram shows the way in which the resistance R and the reactance
X
vary along the transmission line in a repeating pattern. Of course, allowance
must be made for the velocity factor (o.66 - o.8 for typical coaxial cables,
semi-air spaced 0.8 - .95, open wire feeder 0.95 – 0.98), when working
out the wavelength. Use the formula inset above, with f equal
to the frequency in MHz.
IMPEDANCE and SWR
The SWR is constant all along the line but the impedance varies from
point to point. The impedance at a particular point has a resistive part
R and a reactive part X. The values of R and X are fixed by the
SWR and the distance from any point of minimum resistance, which
is used as a convenient zero point.
FOUR NUMBERS.
R for resistance.
X for reactance.
S for SWR
E for distance in electrical degrees. (90° = 1/4 of a wavelength)
from a point of minimum resistance. (positive degrees towards the transmitter).
These four quantities are connected with one another. If you know any
two of them, you can find the other two. For example, if you know R and
X, then you can find S and E, or conversely given S and E you can find
R and X.
This is what the Smith Chart does for you.
DOING WITHOUT THE 'SMITH' CHART
Here are the formulae which allow you to calculate R,X,S or E.
Important
r stands for R/Zo
x stands for X/Zo
t stands for TAN(E)
There are 6 CASES depending on what you know and what you what to find
out.
CASE 1. R and X known.
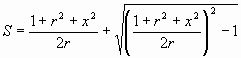
and 
CASE 2. S and E known.
Important S must be greater than 1.
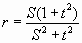
and 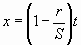
CASE 3. R and S known.
Important., To get a solution S >= r >= 1 or 1/S <= r <=
1
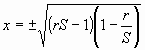
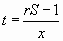
Actually there are two possibilities. Either both x and t are positive
or they are both negative.
CASE 4. X and E known.
Important. To get a solution in this case, t must be greater
than or equal to x, in numerical value, i.e. ignoring +/- signs.
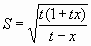
 CASE 5. S and X known.
CASE 5. S and X known.
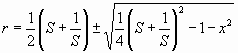
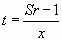
If the quantity under the square-root is negative then there is no
solution. Either S is wrong or X is wrong. The ± sign means that
there are two possible solutions.
CASE 6. R and E known.
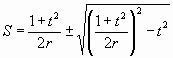
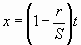
If R < Zo then take the positive signs only.
If R >= Zo then both + and - signs give solutions.
X always has the same sign as t.
SOME LIMITATIONS.
If you try to use these formulae with made up values that don't correspond
to reality, you may run into difficulties. For example you may find you
have to take the square-root of a.negative number.
If this happens, nothing can be done. Your starting values are impossible.
Unfortunately even for some legitimate values you can also run into problems.
This will appear as an attempt to divide by zero. This can be avoided if
you first check to see if you are dealing with one of five special cases
which are specially easy to solve. These cases are:
| |
R |
x |
S |
E |
Answer |
| 1. |
> Zo |
= 0 |
= r |
= 90° |
High resistance, High voltage point |
| 2. |
< Zo |
= 0 |
=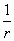 |
=0° |
Low resistance, High current point |
| 3. |
= Zo |
= 0 |
= 1 |
|
A matched line, no point of minimum resistance
and hence no value for E |
| 4. |
= ? |
any value |
= ? |
= 90° |
In this situation X cannot be measured. It seems
to take all values at once. At all other points, R=0 and X=Zo.tan(E) |
| 5. |
= 0 |
Zo.tan(E) |
= ? |
Any (not 90°) |
|
HOW TO USE THE FORMULAE
First check to see if you are dealing with one of the 5 special cases.
If so then the values of the unknowns are as given above. If not then decide
which of the four parameters you know and choose the appropriate formula
for the other two.
Example.
1) A short vertical is tuned to resonance but the SWR measured at the
Tx is still 4:1. What is the impedance of the,antenna? The antenna is fed
with 50 ohm co-ax.
Since the antenna is resonant, the reactance X = 0. Therefore this
is one of the special cases. Short verticals have a low resistance so this
must be special case 2, where R, Zo,X = 0,  and E = 0.
and E = 0.
Therefore 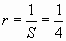 .
Remember that r = R/Zo
.
Remember that r = R/Zo
Therefore 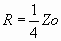 = 12 ½ ohms.
= 12 ½ ohms.
Example 2.
Because of the lack of space a dipole put up for 40 metres is too short.
It is only 58 feet long. It is centre fed with 75 ohm twin which has, a
length of 44 feet. It is found to be impossible to match because of the
high impedance and a check on the SWR shows it to be around 7.5. What can
be done?
Well there are a number of possible solutions, but first of all it helps
to know whats going on.. A check with a Neon suggests that the shack end
of the feeder is at a voltage maximum, so E = 90° here. The velocity
factor of the cable is about 0.71 so one wavelength is about 99 feet 9
inches.
So a 44 foot feeder represents 158.75 electrical degrees.
So at the antenna. E = 90° - 158.75° = -68.75° Remember
that distances measured towards the Tx are positive, so towards the antenna
the distance is considered negative.
Thus we have., S=7.5 E= -68.75° and we can try to find R and X at
the antenna.
This is general case number 2.
Therefore 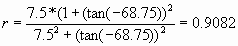
and 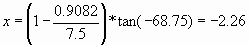
Remember that R = r.Zo and X = x.Zo
Therefore R = 0.9082x75 = 68 ohms approx
and X = -2.26x75 = -169.5 ohms approx
Obviously the problem is the high reactance, and, being negative and
hence capacitive, can be compensated for by coils at the antenna, one in
each leg of the feeder.
For their values wL = 169.5 /2 = 84.75 ohms
Therefore the inductance L needs to be = 1.9 microhenries.
---------- 000000 ---------
SOME OTHER USEFUL FORMULAE.
When dealing with an antenna wire we are dealing with the special case
where R= ? S= ? and E= 90° at the outer end. The reactance at any point,
can be calculated from the formula:
X = Zo . Tan(E)
To estimate Zo use
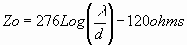 for a
dipole
for a
dipole
or 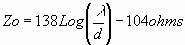 for a single end-fed wire.
---------- 000000 ------~---~
LINE LOSSES.
for a single end-fed wire.
---------- 000000 ------~---~
LINE LOSSES.
When line losses are significant, SWR varies along the line, being greatest
at the load end.
If Sl, S2 are the SWRs at the generator and load ends of the line and
L = the total matched line loss in dBs then,
to calculate Sl from S2:
Calculate: 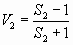 and
and 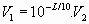
Then 
To do it the other way round, just reverse the calculation procedure.
Back to home page